ベクトルとは？誰でも理解できるように簡単に解説

ベクトルとは、一般的には「大きさと向きをもつ量」であり「矢印で表すことのできる量」と説明されます。

ただし、この説明は物理学的な視点に立ったときの解釈です。実際は、ベクトルはさまざまな分野で異なった使い方をされている概念であるため、その定義を一言で表すことはできません。

たとえば物理学においては世の中のありとあらゆる物体運動を理解するための矢印ですが、コンピューター・サイエンスにおいては機械学習やCG（コンピューター・グラフィックス）で重要な役割を果たす特別なデータです。そして数学においては線形代数の中心的な概念の一つです。

このようにベクトルは分野によって使われ方が異なります。そのため、すべての分野で通用する定義をしようとすると、どうしても無理が出てきてしまうのです。

ただし異なる点があれば、すべての分野に共通する性質もベクトルにはあります。そして最終的には、分野ごとに異なる抽象的な定義にこだわるよりも、すべての分野に共通の性質に注目することが、「ベクトルとは何か」ということを理解するためのカギとなります。

つまり、ベクトルの本質は、その定義よりも性質にあるのです。

最初から難しそうな話になってしまいましたが、当ページでは「ベクトルとは何か」ということについて、これらすべての学問分野で通用するような理解を得られるように解説していきます。さらに理解を深めるために、アニメーションを活用しながら視覚的にも解説していきます。

ぜひ、じっくりとご覧になってみてください。必ずや・・・、ベクトルとは何かということを深く理解するための大きな助けとなることでしょう。

1. ベクトルの意味

冒頭でも述べた通り、ベクトルの意味は学校では「大きさと向きをもつ量」であり「矢印で表すことができる量」であると説明されます。まずは、この一般的な解釈についておさらいしておきましょう。

たとえば、私たちが普段の生活の中で使う「温度」や「重さ」といった量は、大きさがあるだけで向きはありません。一方で「速度」や「力」といった量は、大きさだけではなく向きも含んでいます。

このことから、「温度」や「重さ」は、「速度」や「力」と比べると、性質が根本的に異なるものであると言えます。そのため、学問の世界では、大きさだけをもつ量のことを「スカラー」、大きさと向きの二つをもつ量のことを「ベクトル」というように呼び分けることになっています。

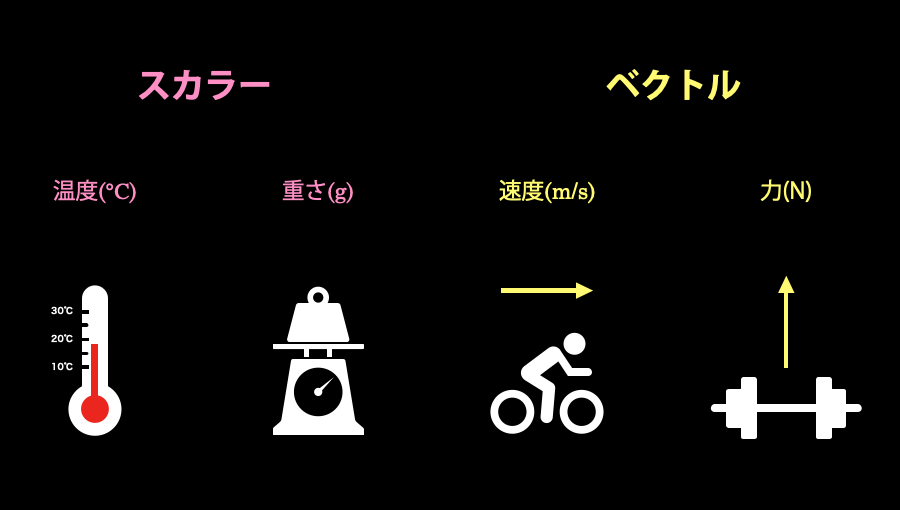
また上の画像から確認できる通り、ベクトルは、何らかの量の大きさ・向きを矢印の長さ・方向で表します。この矢印は、イメージとしては、以下のアニメーションのように、「方向性をもった流れを表すもの」というように考えると良いでしょう。

このようにベクトルは大きさ・向きの二つの属性をもっており、現実世界の様々な物体運動の分析のために欠かせない概念となっています。

以上が義務教育で習う一般的なベクトルの意味です。

もちろん一般教養としては、ここまで説明した理解で十分です。しかし、ベクトルというものを本質的に理解しようとする場合は、この説明では問題があります。なぜなら、義務教育ではコンピューター・サイエンス（機械学習やCGなど）や、線形代数を習わないため、この一般的なベクトルの説明には、それらの視点が含まれていないからです。

それでは、それぞれの学問分野ではベクトルはどのように定義されているのでしょうか。次からこの点について見ていきましょう。

2. ベクトルの定義

繰り返しになりますが、上で説明した一般的なベクトルの解釈は、物理学的な視点に立った場合のものです。それでは異なる学問分野では、ベクトルは一体どのように定義されているのでしょうか。

2.1. 学問分野ごとの定義

ベクトルの定義は、物理学・コンピューターサイエンス・数学ごとに、それぞれ次のように解釈されています。

それぞれの定義の違いと詳細は、文字だけで理解しようとするよりも、以下のアニメーションで視覚的な助けも借りる方が断然理解しやすいので、ぜひご覧ください。

このように物理学では、ベクトルは長さと向きの二つの属性をもち、空間内のあらゆるところに存在できる矢印であると考えます。そしてコンピューターサイエンスでは、ベクトルは単なる数値のリストであると考えます。最後に数学では、物理の視点とコンピューターサイエンスの視点の双方を一般化して、ベクトルの足し算や掛け算などの概念を導き出し、計算可能なものにしようとします。

2.2. 線形代数における定義

それでは、当サイトのメインテーマの一つである線形代数においては、ベクトルはどのように解釈すれば良いでしょうか。

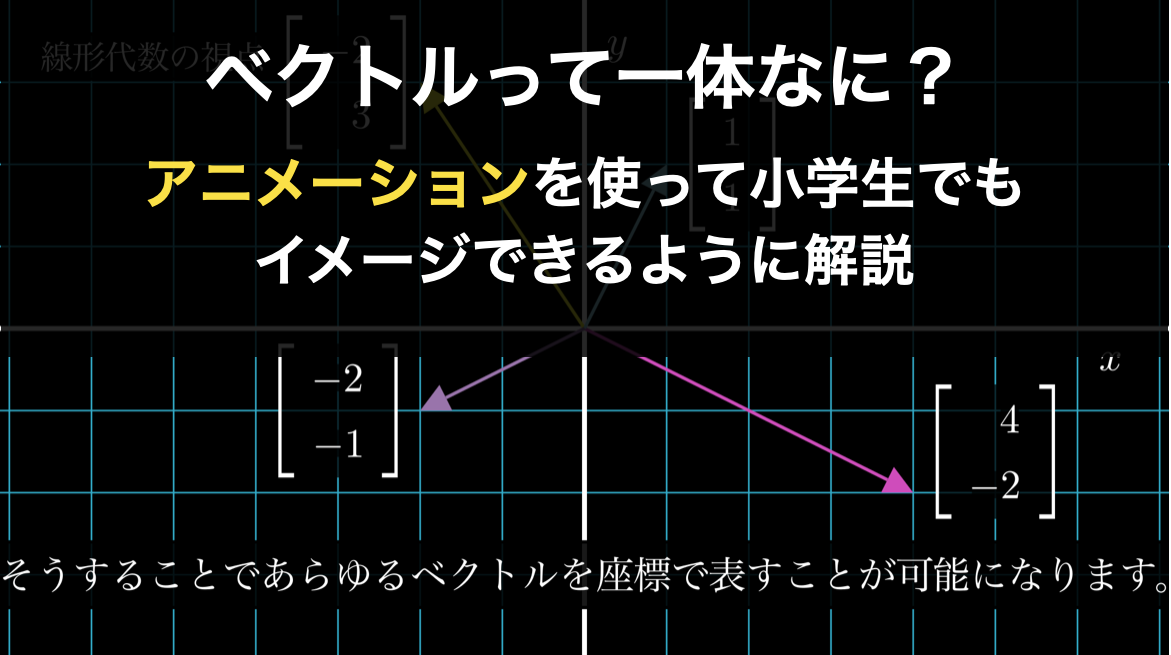
線形代数では、基本的に物理学のように「ベクトルは長さと向きをもつ矢印である」と考えると良いです。ただし物理学では、この矢印は空間のあらゆるところに自由に存在することができますが、線形代数では \(x\) 座標、\(y\) 座標などで示す「座標系」の中に存在するものであり、ベクトルの始点は常に原点 \((0, 0)\) にあります。

これも以下のアニメーションを見ていただくことで、はっきりとイメージできるようになります。

このように理解することで、ベクトルを、コンピュータサイエンスのように数値のリスト(座標)で統一して表すことができ、さまざまな重要な計算がやりやすくなります。

3. 全ての分野に共通のベクトルの性質

さて、ここまで見てきたように、ベクトルの定義は学問分野によって異なります。しかし、そのままでは問題があります。なぜなら、このように定義が異なっていると、たとえば物理学者、コンピューター・サイエンス学者、数学者の間で学問分野を飛び越えて議論しようとしたときに、お互いに混乱することになってしまうからです。

そこで、そのようなときは、それぞれの分野ごとに共通する性質を見出して、その性質を何があっても揺るがない根本的なルール（＝公理）とし、この公理を大前提として話し合うことで混乱を防ぐことができます。

それでは全ての学問分野に共通するベクトルの性質とは何でしょうか。

それは以下の８つです。

これらの性質についての具体的な説明は、以下の２つのページで行っています。

• 『ベクトルの和とは何か？誰でもわかる幾何学的な意味と計算方法の解説』
• 『ベクトルの掛け算とは何か？幾何学的な意味と計算方法の解説』

そのためこれらの性質を当ページで覚えようとする必要はありませんし、理解できなかったとしても全く問題ありません。当サイトの線形代数のページを読み進めていくうちに自然と身につきます。

ここでは、「ベクトルとはこれらの８つの性質をもつ概念である」とすることで、「ベクトルとは何か」という学問分野ごとに解釈が異なる論争に悩まされることなく、誰でもベクトルについて話すことができるようになる、ということを理解するようにしましょう。

この公理を前提とすれば、それこそ、物理学者とコンピュータサイエンス学者の間でも、数学者と物理学者の間でも、何の問題もなくベクトルについて議論することができます。

ということはベクトルとは、文字で厳密に定義できるようものではなくて、本質的にはこの８つの性質をもつ概念であると言えます。

繰り返しになりますが、この点について最初からハッキリと理解しようとする必要は全くありません。まずは当サイトの線形代数の解説ページを、どうぞ読み進めていってみてください。そしてすべて読み終わった後に、あらためて、この公理に立ち戻ってみてください。

そうすると、なぜ、ベクトルを文字で定義しようとすると抽象的になってしまうのかが理解できるようになっていることでしょう（実際はベクトルだけでなく、数学的概念のほとんどが文字で表すと抽象的になってしまうのですが、その理由も同じように理解することのなります）。そして、ベクトルとは、この8つの性質を持つ概念であるということが理解できるようになっていることでしょう。

それが分かれば科学的思考とはどういうものなのかを体得することができます。そして、それは人生のあらゆる面において、とてつもなく大きな価値をもたらしてくれます。

4. まとめ

以上が「ベクトル」です。

ぜひ、学習が進んだ後にもまた読み返してみてください。学習が進むたびに、より具体的に理解できるようになっていきます。