基底ベクトルとは、簡潔に言うなら「空間上のあらゆるベクトルを v=xa+yb のかたちで表すことを可能にするベクトル a, b の組み合わせ」のことです。言葉だけでも理解できないことはないですが、そこからこの意味するところを具体的にイメージするのは難しいと思います。
そこで、このページではこの基底ベクトルについてアニメーションを使いながら誰でもわかるように解説します。ぜひ学習のお役に立てばと思います。
目次
1. 基底ベクトルとは
「ベクトルの分解とは」では、\(\hat{\imath}\) （アイハット）と \(\hat{\jmath}\) （ジェイハット）の２本のベクトル を使って、\(\vec{v}=x\hat{\imath}+y\hat{\jmath}\) という式で２次元ベクトルを表しました。そして、\(\hat{\imath}\) と \(\hat{\jmath}\) は以下のように、長さが１の水平ベクトルと垂直ベクトルでした。
\[\begin{eqnarray}
\hat{\imath}=
\left[ \begin{array}{c} 1 \\ 0 \end{array} \right],
\hspace{3mm}
\hat{\jmath}=
\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]
\end{eqnarray}\]
実は、この \(\hat{\imath}\) と \(\hat{\jmath}\) は「基底ベクトル」という特別な名前で呼ばれます。基底ベクトルとは、「空間上のあらゆるベクトルを分解して表すことを可能とするベクトルの組み合わせ」のことです。
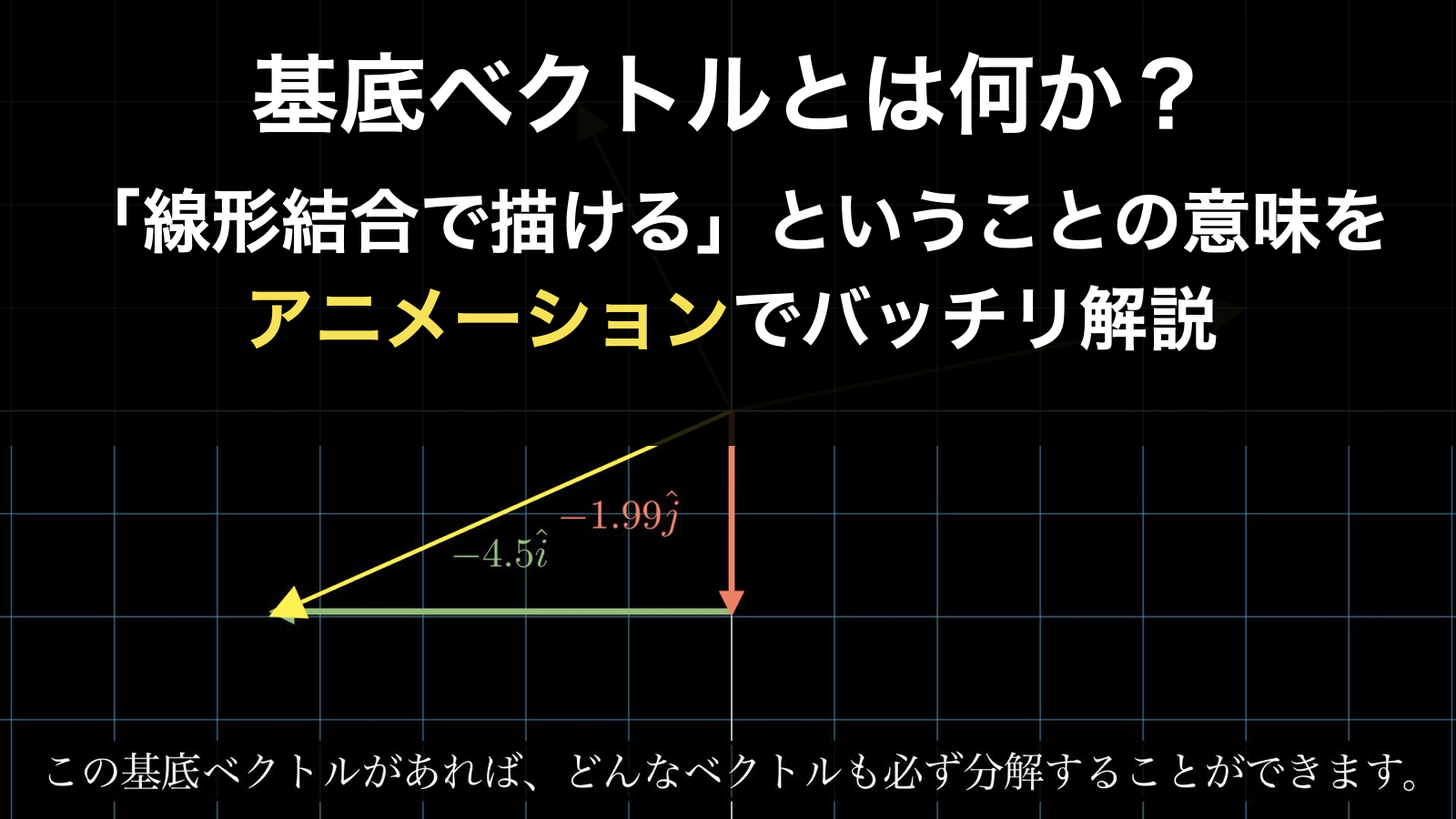
以下のアニメーションでこのことを幾何学的に理解することができますので是非ご覧ください。
このように「空間上のあらゆるベクトルを \(x\hat{\imath}+y\hat{\jmath}\) のかたちで表すことを可能とするベクトルの組み合わせ」が基底ベクトルです。２次元空間では、２本の基底ベクトルがあれば、どのようなベクトルでも描くことができます。同じように３次元空間では、３本の基底ベクトルがあれば、どのようなベクトルでも描くことができます。
ポイント
基底ベクトルは、「空間上のあらゆるベクトルを \(x\hat{\imath}+y\hat{\jmath}\) のかたちで表すことを可能とするベクトルの組み合わせ」。なお、3次元空間の場合は、\(x\hat{\imath}+y\hat{\jmath}+z\hat{k}\) になります。
2. 様々な基底ベクトル
さて、ここまでは \(\hat{\imath}\) と \(\hat{\jmath}\) を基底ベクトルとして用いてきました。しかし実は基底ベクトルは、これに決まっているわけではありません。
定義上、既定ベクトルは「空間上のあらゆるベクトルを \(x\hat{\imath}+y\hat{\jmath}\) で表すことを可能とするベクトルの組み合わせ」であり、そのような組み合わせは無限に存在するのです。この点について、以下のアニメーションで確認しましょう。
このように、ほとんどどのようなベクトルのペアでも基底ベクトルとして機能します。
なお基底ベクトルとしては、\(\hat{\imath}\) と \(\hat{\jmath}\) が断然わかりやすいです。そのため「なぜわざわざ別のわかりづらい基底ベクトルを扱うようなことが必要なのか？」と疑問に思われるかもしれません。
これについては、さまざまな基底ベクトルで空間を認識できるようになると、線形変換をとてもよくイメージできるようになるという利点があるのです（もちろん現時点では、そこまでできる必要はありません。学習を進める中で自然とできるようになっていきます）。
なお、中には基底ベクトルになれない組み合わせも存在するのですが、これがまた線形代数において重要な意味を持ちます。
ただし、ここでは深く考えずに、「基底ベクトルになりえるベクトルの組み合わせは無限にある」ということを覚えておきましょう。
3. 練習問題
それでは最後に基底ベクトルに関する練習問題を用意しておきます。しかし、実のところ、現時点でこの問題を解けるようになっている必要はありません（特に【練習問題②】）。そのため、最初は確認の意味で眺めておく程度でまったく問題ありません。もしかしたら難しく感じるかもしれませんが、必要な項目を理解した後で見返したら、とても簡単なものであることがわかるのでご安心ください。
【練習問題①】 異なる基底ベクトルによる分解表示
問題：
以下のベクトル \(\vec{a}\)を、①基底ベクトル \(\hat{\imath}\)・\(\hat{\jmath}\) の組み合わせ、②基底ベクトル \(\vec{v}\)・\(\vec{w}\) の組み合わせで表せ。
\[\begin{eqnarray}
\vec{a}=\left[ \begin{array}{c} 4 \\ 1 \end{array} \right]\\
\end{eqnarray}\]
\[\begin{eqnarray}
\hat{\imath}=\left[ \begin{array}{c} 1 \\ 0 \end{array} \right],
\hspace{3mm}
\hat{\jmath}=\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]
\end{eqnarray}\]
\[\begin{eqnarray}
\vec{v}=\left[ \begin{array}{c} 1 \\ 2 \end{array} \right],
\hspace{3mm}
\vec{w}=\left[ \begin{array}{c} 3 \\ -1 \end{array} \right]\\
\end{eqnarray}\]
解答：
\[\begin{eqnarray}
\left[ \begin{array}{c} 4 \\ 1 \end{array} \right]
=
4\left[ \begin{array}{c} 1 \\ 0 \end{array} \right]
+
1\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]
\hspace{3mm}
\Rightarrow
\hspace{3mm}
\vec{a}=4\hat{\imath}+1\hat{\jmath}
\end{eqnarray}\]
\[\begin{eqnarray}
\left[ \begin{array}{c} 4 \\ 1 \end{array} \right]
=
1\left[ \begin{array}{c} 1 \\ 2 \end{array} \right]
+
1\left[ \begin{array}{c} 3 \\ -1 \end{array} \right]
\hspace{3mm}
\Rightarrow
\hspace{3mm}
\vec{a}=1\vec{v}+1\vec{w}
\end{eqnarray}\]
【練習問題②】 異なる基底ベクトルによる分解表示
問題：
以下のベクトル \(\vec{a}\)を、①基底ベクトル \(\hat{\imath}\)・\(\hat{\jmath}\) の組み合わせ、②基底ベクトル \(\vec{v}\)・\(\vec{w}\) の組み合わせで表せ。
\[\begin{eqnarray}
\vec{a}=\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]\\
\end{eqnarray}\]
\[\begin{eqnarray}
\hat{\imath}=\left[ \begin{array}{c} 1 \\ 0 \end{array} \right],
\hspace{3mm}
\hat{\jmath}=\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]
\end{eqnarray}\]
\[\begin{eqnarray}
\vec{v}=\left[ \begin{array}{c} 1 \\ 2 \end{array} \right],
\hspace{3mm}
\vec{w}=\left[ \begin{array}{c} 3 \\ -1 \end{array} \right]\\
\end{eqnarray}\]
解答：
\[\begin{eqnarray}
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
=
1\left[ \begin{array}{c} 1 \\ 0 \end{array} \right]
+
1\left[ \begin{array}{c} 0 \\ 1 \end{array} \right]
\hspace{3mm}
\Rightarrow
\hspace{3mm}
\vec{a}=1\hat{\imath}+1\hat{\jmath}
\end{eqnarray}\]
\[\begin{eqnarray}
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
=
\dfrac{4}{7}
\left[ \begin{array}{c} 1 \\ 2 \end{array} \right]
+
\dfrac{1}{7}
\left[ \begin{array}{c} 3 \\ -1 \end{array} \right]
=
\left[ \begin{array}{c} \frac{4}{7}+\frac{3}{7} \\ \frac{8}{7}+(-\frac{1}{7}) \end{array} \right]
\hspace{3mm}
\Rightarrow
\hspace{3mm}
\vec{a}=\dfrac{4}{7}\vec{v}+(-\dfrac{1}{7})\vec{w}
\end{eqnarray}\]
解説：
実際のところ、現段階ではこの問題は解けなくても構いません。なぜなら、これを解くには、基底変換（線形変換）や行列、逆行列の理解が必要だからです。以下に解答のプロセスを書いておきますので、学習が進んだ後に見返して見ましょう。そうすれば、それぞれの計算にどのような意味があるのかが理解できるようになっていることでしょう。
① \(\vec{v}\) と \(\vec{w}\) を列ベクトルとした行列 \(M\) を作る（これは基底ベクトル \(\hat{\imath}\) と \(\hat{\imath}\) のペアを、\(\vec{v}\) と \(\vec{w}\) のペアに変換する行列を作ることを意味しています） 。
\[\begin{eqnarray}
M=\left[ \begin{array}{c} 1 & 3 \\ 2 & -1 \end{array} \right]\\
\end{eqnarray}\]
② 行列 \(M\) の逆行列 \(M^{-1}\) を求める（これは基底ベクトル \(\vec{v}\) と \(\vec{w}\) のペアを、 \(\hat{\imath}\) と \(\hat{\imath}\) のペアに変換する行列を作ることを意味しています）。
\[\begin{eqnarray}
M^{-1}=\left[ \begin{array}{c} \frac{1}{7} & \frac{3}{7} \\ \frac{2}{7} & -\frac{1}{7} \end{array} \right]\\
\end{eqnarray}\]
③ \(M^{-1}\) と \(\vec{a}\) の積を求める（これは基底ベクトル \(\hat{\imath}\) と \(\hat{\imath}\) のペアで表していた座標を、基底ベクトル \(\vec{v}\) と \(\vec{w}\) のペアで表した場合の座標に変換することと同じです）。
\[\begin{eqnarray}
M^{-1}\vec{a}=
\left[ \begin{array}{c} \frac{1}{7} & \frac{3}{7} \\ \frac{2}{7} & -\frac{1}{7} \end{array} \right]
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
=
\left[ \begin{array}{c} \frac{4}{7} \\ \frac{1}{7} \end{array} \right]
\end{eqnarray}\]
この最終項のベクトルの第一成分が基底ベクトル \(\vec{v}\) の係数、第二成分が基底ベクトル \(\vec{w}\) の係数です。
4. まとめ
以上が基底ベクトルです。繰り返すと、基底ベクトルとは『空間上のあらゆるベクトルを「 \(x\hat{\imath}+y\hat{\jmath}\)」 で表すことを可能とするベクトルの組み合わせ（3次元空間では「 \(x\hat{\imath}+y\hat{\jmath}+z\hat{k}\)」）』です。
当ページが理解を深めるための役に立ったなら嬉しく思います。
次に読みたいページ
ここまでで解説してきた基底ベクトルとベクトルの和・掛け算・分解を理解したら、線形代数における中心的な概念である、線形結合というものを理解することができます。ここからどんどん線形代数の領域に入っていきます。内容的には、このページで解説したことと非常に似通っているのですが、あらためてこれを線形結合という概念とともに理解することが役立ちます。『線形結合とは何か？アニメーション付きで誰でもわかるように解説』で解説しているのでぜひご覧ください。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント
コメント一覧 （2件）
① ⃗v と ⃗w を列ベクトルとした行列 M を作る（これは基底ベクトル ^ı と ^ı のペアを、⃗v と ⃗w のペアに変換する行列を作ることを意味しています） 。
^ı と ^ı → ^ı と ^j ではないでしょうか？
大変わかりやすく、また理解に役に立つ記事です。