一様分布は、離散型でもあり連続型でもある確率分布です。ある試行のすべての事象の確率が均一である場合の分布であり、非常に単純なものですが、ベイズ統計において事前情報が何もない場合の事前分布として使われるという点で有用です。
当ページでは、この一様分布について簡潔に解説します。
1. 一様分布とは
一葉分布とは、ある試行のすべての事象の確率が同じである場合の分布です。
たとえばスイカ割りのために、目隠しをしたままグルグル回され、デタラメに止まるとすると、止まった角度が北から右に何度であるかは、0 から 360 の範囲の連続一様分布で表すことができます。
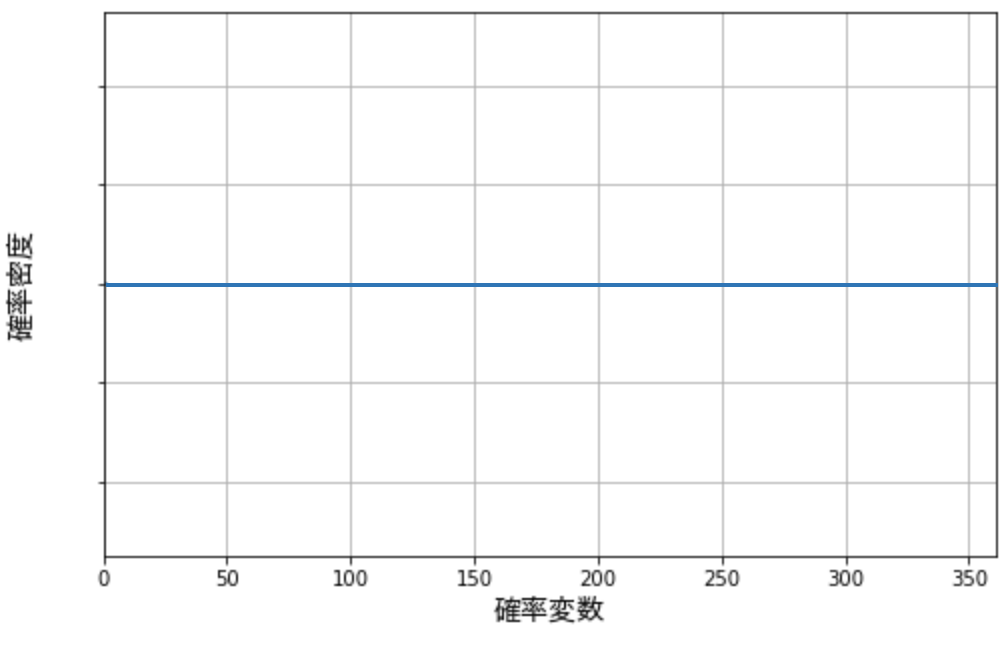
このように水平なグラフを描くのが一様分布です。
2. 一様分布の確率関数
確率変数を \(x\)、確率変数の範囲を \(α≤x≤β\) とすると、連続型の一様分布の確率密度関数は以下の通り定義されます。
一様分布の確率密度関数
\[
f(x|α,β)
=
\dfrac{1}{β-α}
\]
上のスイカ割りの例で言うと、0° から 30° の方向を向いている確率は、この確率密度関数から、次のように簡単に求められます。
まず確率密度関数は以下の通りになります。
\[\begin{eqnarray}
f(x|0, 360)= \dfrac{1}{360-0}
\end{eqnarray}\]
そして 0° から 30° の方向を向いている確率は積分を使って次のように計算できます。
\[\begin{eqnarray}
F(30|0, 360) – F(0|0,360) = \dfrac{30-0}{360-0}=\dfrac{1}{12} \approx 0.0833
\end{eqnarray}\]
ベイズ統計においては、特に \(α=0\), \(β=1\) の一様分布が、事前確率分布として使われる場合が多いため重要です。
3. 一様分布の期待値
一葉分布の期待値は以下の計算で求められます。
一様分布の期待値
\[\begin{eqnarray}
E(X)=\dfrac{\alpha + \beta}{2}
\end{eqnarray}\]
4. 一様分布の分散
一葉分布の分散は以下の計算で求められます。
一様分布の分散
\[\begin{eqnarray}
V(X)=\dfrac{1}{12}(\beta – \alpha)^2
\end{eqnarray}\]
5. 一様分布のまとめ
以上のように一様分布は非常に単純な確率分布です。連続確率分布のとっかかりとして知っておくと良いでしょう。

コメント