このページでは、Pythonのsetの基本的な操作を網羅してまとめています。
Pythonのsetは、主に数学の集合演算を簡単に行うことができるオブジェクトです。ここでしっかりと身につけておきましょう。
1. set(集合)の作成
それでは、まずはsetの作成方法から見ていきましょう。作成方法を理解すると、setがどのようなデータをもつオブジェクトなのかの理解も深まっていきます。
1.1. 波括弧 {} で作成
setは、値が重複しない要素を格納するミュータブル(変更可能)なオブジェクトで、波括弧 {} の中に値をカンマ区切りで入力して作成します。
以下のコードをご覧ください。
set = {1, 1, 2, 2.0, 3, 3.00, 4, 4.000}
print(set)
このようにsetでは同一の要素は重複できないので、同じ値が複数ある場合1つだけ格納されます。なお、整数の2や、浮動小数点の2.0も同じ値としてみなされます。
また、setは異なる型の要素を同時に格納することができますしタプルも格納することができます。ただしミュータブル(変更可能)なオブジェクトは格納できません。
set = {1, (1,2,3), '二', (4, '五', 6.0)}
print(set)
さらに、setはインデックス番号で要素を管理しているのではないため、要素の順序はありません。上のコードでも、set作成時の要素の順番と出力された順番が異なりますね。
ここまで出てきたsetの特徴をまとめてみましょう。
- setに同一の要素は重複できない。
- setにミュータブルな要素は格納できない。
- setに要素の順序はない。
このような特徴があるのは、setは数学的な集合演算を行うためのオブジェクトだからです。集合演算については後ほど解説します。
1.2. set()関数で作成
setはset()関数でも作成することができます。
1.2.1. 空のsetの作成
空のsetを作りたい時は、set()関数を使う必要があります。なぜなら、波括弧 {} だけで、要素を指定しなかった場合、次のように辞書型オブジェクトになるからです。
辞書については「Pythonの辞書(dict)の使い方と知っておくべき操作方法」をご覧ください。
dict = {}
print(dict)
print(type(dict))
そのため、空のsetを作りたい場合はset()関数を使う必要があります。set()関数の引数を空白にすると空のsetが作成されます。
set = set()
print(set)
print(type(set))
1.2.2. 別のオブジェクトからsetを作成
set()関数の引数にリストやタプルなどのイテラブルなオブジェクトを渡すと、それをsetに変換します。
list = [0, 1, 1.0, -1, 2, -2, 3, 3.00, -3, 3.0, 4, -4, -4, 5, -5]
set1 = set(list)
print(set1)
引数に辞書を渡す場合は、辞書型メソッドのkeys()、values()、items()を使って、辞書のキーや値のどれを変換するのかを指定します。
これらのメソッドについては「Pythonの辞書(dict)のキー・値の存在確認と取得方法」で解説しています。
dict = {'東京':900, '横浜':370, '大阪':250, '名古屋':230, '福岡':150}
set2 = set(dict.keys())
print(set2)
set3 = set(dict.values())
print(set3)
set4 = set(dict.items())
print(set4)
1.2.3. frozenset()関数でイミュータブルなsetを作成
frozenset()関数を使うと、イミュータブル(変更不可能)なsetを作ることができます。
これで作ったsetは、後で解説するような要素の追加や削除などができないsetになります。そのため、要素を変更してはいけないsetを作る時に使います。
使い方はset()関数と全く同じです。
list = [0, 1, 1.0, -1, 2, -2, 3, 3.00, -3, 3.0, 4, -4, -4, 5, -5]
set = frozenset(list)
print(set)
1.3. 集合内包表記で作成
setもリストと同じように内包表記で作成することができます。リスト内包表記の場合の角括弧 [] を波括弧 {} にするだけです。
具体的な書き方については、「Pythonのリスト内包表記の書き方」を参考にしてください。
set = {i**2 for i in range(5)}
print(set)
2. setの要素の追加|add()メソッド
setに要素を追加するには、add()メソッドを使います。
以下のコードでは、最初に空のsetを作成して、add()メソッドで要素を追加しています。
colors = set()
colors.add("red")
colors.add("orange")
print(colors)
setは重複した値を持つことはできないため、重複した値をadd()メソッドで追加しようとしても無視されます。
colors.add("red")
print(colors)
3. setの要素の削除
setの要素を削除するには、次の4つの方法があります。
- remove()メソッド
- discard()メソッド
- pop()メソッド
- clear()メソッド
それぞれ見ていきましょう。
3.1. 指定の要素の削除(エラーあり)|remove()メソッド
remove()メソッドは、引数で削除する要素を指定します。
num_set = {1, 2, 3, 4, 5}
num_set.remove(5)
print(num_set)
もし、存在しない要素を指定した場合はキーエラーになります。
num_set.remove(6)
3.2. 指定の要素の削除(エラーなし)|discard()メソッド
discard()メソッドも、引数で削除したい要素を指定します。
num_set = {1, 2, 3, 4, 5}
num_set.discard(5)
print(num_set)
remove()メソッドとの違いは、存在しない値を指定した場合です。discard()メソッドの場合はエラーにはならずに、そのまま無視されます。
num_set.discard(6)
print(num_set)
3.3. 要素をランダムに取り出して削除|pop()メソッド
pop()メソッドでもsetの要素を削除することができます。
ただし、リストや辞書のpop()メソッドと違って、setのpop()は削除する要素を引数で指定することはできません。
setからランダムに要素を取り出して削除します。
なお、リストや辞書のpop()メソッドは、「Pythonのpop()でリストや辞書の要素を削除する方法」で解説しています。
num_set = {1, 2, 3, 4, 5}
popped = num_set.pop()
print(num_set)
print(popped)
このように、pop()メソッドの戻り値は、削除した要素なので、それを別の変数に入れて出力することができます。
3.4. 全ての要素を削除|clear()メソッド
clear()メソッドは、setの要素を全て削除して空にします。
num_set = {1, 2, 3, 4, 5}
num_set.clear()
print(num_set)
4. 集合演算
続いて、setの独特の機能である集合演算について解説していきます。setでは、以下の集合演算を行うことができます。
- 和集合
- 差集合
- 積集合
- 対称差集合
早速見ていきましょう。
4.1. 和集合|+演算子, union()
和集合は下図のように、二つ以上の集合に含まれている全ての要素を集めたものです。
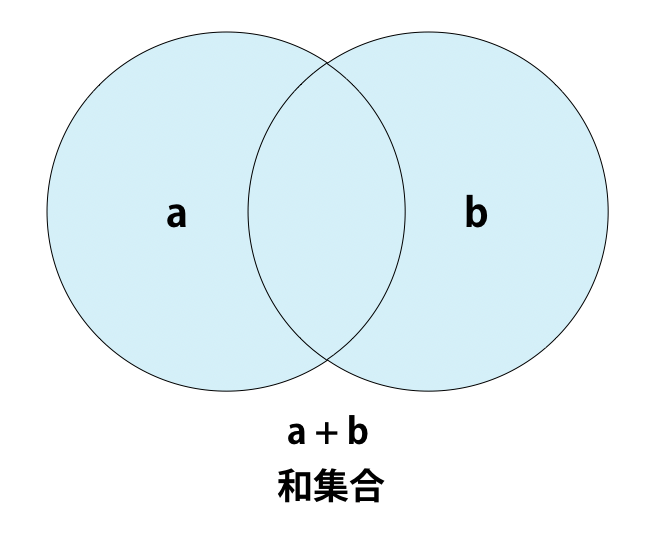
Pythonでは和集合を求めるには、次の4つの方法があります。
- |演算子
- union()メソッド
- =|演算子
- update()メソッド
まず |演算子を使うと、複数のsetの全ての要素を格納した新しいsetを作ることができます。
s1 = {0, 1}
s2 = {1, 2}
s3 = {3, 4}
union = s1 | s2 | s3
print(union)
union()メソッドは|演算子と同じです。しかし、|演算子はset型オブジェクト同士でなければいけないのに対して、union()メソッドの引数にはset以外のイテラブルを渡すことができます。
s1 = {0, 1}
l1 = [1, 2]
t1 = (3, 4)
union = s1.union(l1, t1)
print(union)
|= 演算子は、既存のsetを和集合で上書きします。
s1 = {0, 1}
s2 = {1, 2}
s3 = {3, 4}
s1 |= s2
s1 |= s3
print(s1)
update()メソッドは|=演算子と同じですが、引数にはset以外のオブジェクトを渡すことができます。
s1 = {0, 1}
l1 = [1, 2]
t1 = (3, 4)
s1.update(l1, t1)
print(s1)
4.2. 差集合|-演算子, difference()
差集合は複数の集合のうち、任意の一つの集合にしか含まれていない要素を集めたものです。
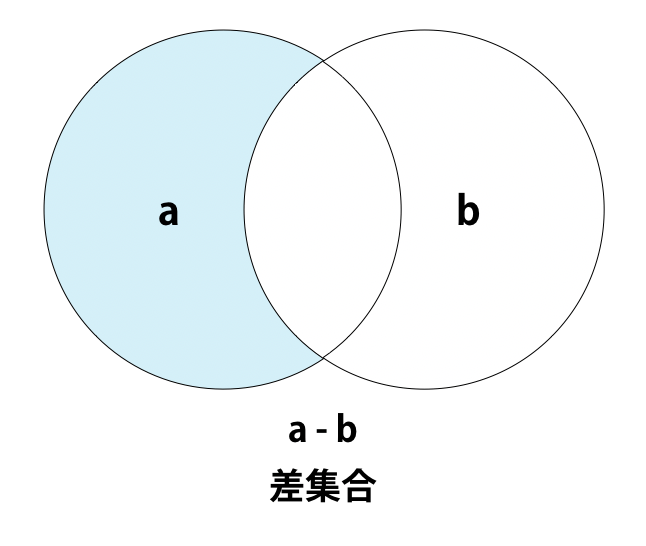
Pythonで差集合を求める方法は次の4つあります。
- -演算子
- difference()メソッド
- -=演算子
- difference_update()メソッド
-演算子を使うと、複数のsetのうち任意のsetにしか含まれていない要素を取り出した新しいsetを作ることができます。
s1 = {0, 1}
s2 = {1, 2}
s3 = {2, 3}
set_difference = s1 - s2 - s3
print(set_difference)
difference()メソッドは-演算子と同一ですが、-演算子はset同士でなければいけないのに対し、difference()メソッドの引数には、リストやタプルを渡すことができます。
s1 = {0, 1}
l1 = [1, 2]
t1 = (2, 3)
set_difference = s1.difference(l1, t1)
print(set_difference)
-=演算子は、左辺の既存のリストを差集合で上書きしていきます。
s1 = {0, 1}
s2 = {1, 2}
s3 = {2, 3}
s1 -= s2
s1 -= s3
print(s1)
difference_update()メソッドは-=演算子と同様ですが、引数にはリストやタプルなどのイテラブルも渡すことができます。
s1 = {0, 1}
l1 = [1, 2]
t1 = (2, 3)
s1.difference_update(l1, t1)
print(s1)
4.3. 積集合|&演算子, intersection()
積集合は複数の集合の中に含まれている同一の要素を集めたものです。
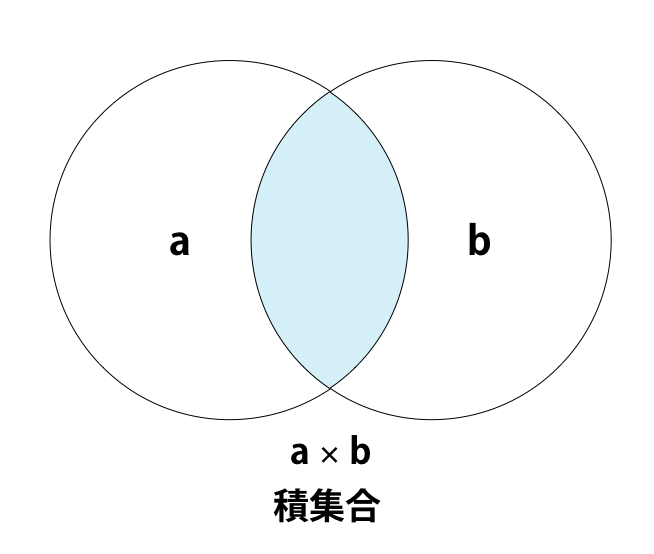
Pythonで積集合を求めるには、次の4つの方法があります。
- &演算子
- intersection()メソッド
- &=演算子
- intersection_update()メソッド
&演算子を使うと、複数のsetに含まれている同一の要素のみを取り出した新しいsetを作ることができます。
s1 = {0, 1, 2}
s2 = {1, 2, 3}
s3 = {2, 3, 4}
intersection = s1 & s2 & s3
print(intersection)
intersection()メソッドは、&演算子と同一ですが、&演算子はset同士でしかいけないのと異なり、intersection()メソッドの引数には、リストやタプルなどのイテラブルを渡すことができます。
s1 = {0, 1, 2}
l1 = [1, 2, 3]
t1 = (2, 3, 4)
intersection = s1.intersection(l1, t1)
print(intersection)
&=演算子は新しいsetを作るのではなく、左辺のsetを積集合で更新します。
s1 = {0, 1, 2}
s2 = {1, 2, 3}
s3 = {2, 3, 4}
s1 &= s2
s1 &= s3
print(s1)
intersection_update()メソッドは、&=演算子と同じですが、引数にはset以外のイテラブルを渡すことができます。
s1 = {0, 1, 2}
l1 = [1, 2, 3]
t1 = (2, 3, 4)
s1.intersection_update(l1, t1)
print(s1)
4.4. 対称差集合|^演算子, symmetric_difference()
対称差集合は、それぞれの集合にしか属さない要素を集めたものです。
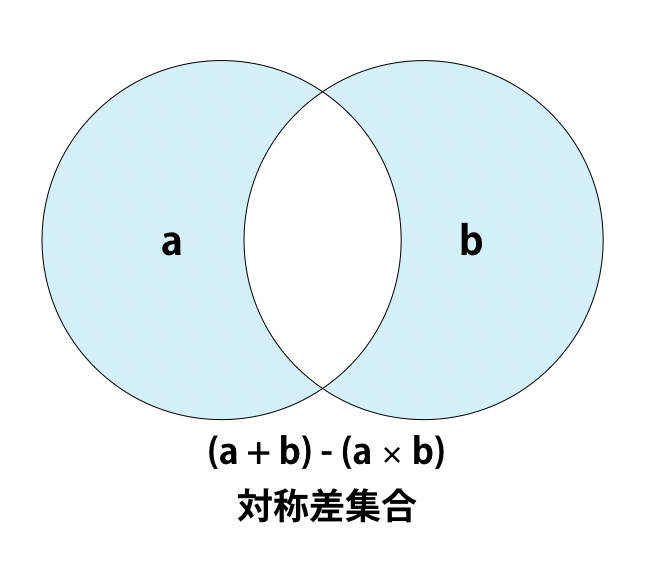
Pythonでは対称差集合は、次の4つの方法で求めることができます。
- ^演算子
- symmetric_difference()メソッド
- ^=演算子
- symmetric_difference_update()メソッド
まず^演算子を使うと、set同士の対称差集合の要素を取り出した新しいsetを作ることができます。
s1 = {0, 1, 2}
s2 = {1, 2, 3}
symmetric = s1 ^ s2
print(symmetric)
symmetric_difference()メソッドでは、引数に渡すものはset以外のイテラブルでも構いません。
s1 = {0, 1, 2}
l1 = [1, 2, 3]
symmetric = s1.symmetric_difference(l1)
print(symmetric)
^=演算子は、左辺のsetを対称差集合で上書きします。
s1 = {0, 1, 2}
s2 = {1, 2, 3}
s1 ^= s2
print(s1)
symmetric_difference_update()メソッドでは、引数にset以外のイテラブルを渡して、対称差集合で上書きすることができます。
s1 = {0, 1, 2}
l1 = [1, 2, 3]
s1.symmetric_difference_update(l1)
print(s1)
5. set同士の要素の比較
ここでは、set同士の要素の比較方法について解説します。
5.1. 完全一致の判定|==演算子
複数のsetの要素が完全に一致しているかどうかを調べるには==演算子を使います。
下図のように要素が完全に一致していればTrueを返し、それ以外の場合はFalseを返します。
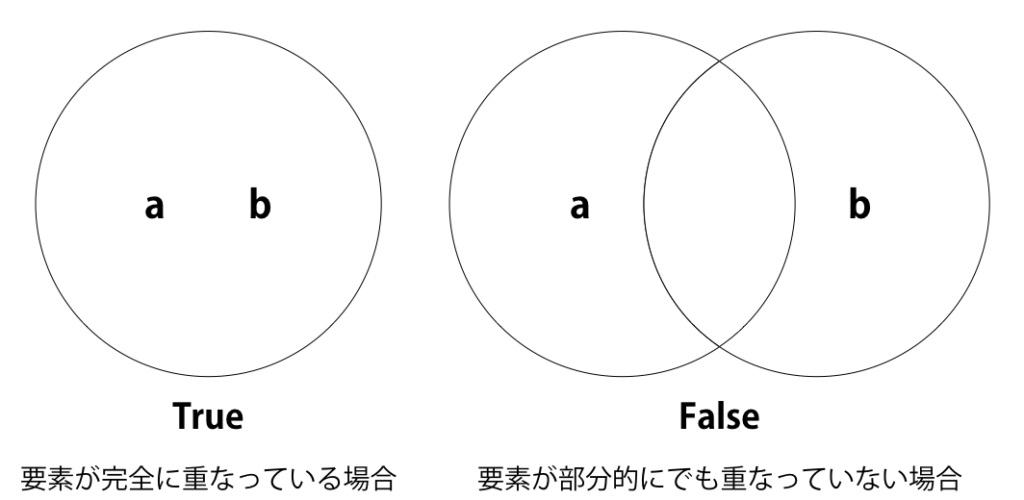
なお、setには要素の順番はないので、並びは関係ありません。
s1 = {1, 2, 3}
s2 = {3, 2, 1}
s3 = {1, 2, 3, 4}
print(s1==s2)
print(s1==s3)
5.2. 完全不一致の判定|isdisjoint()メソッド
複数のsetに共通の要素が1つでもあるかどうか(完全不一致かどうか)を判定するには、isdisjoint()メソッドを使います。
このメソッドは下図のように、共通の要素が1つもない場合にTrueを返し、それ以外の場合にFalseを返します。
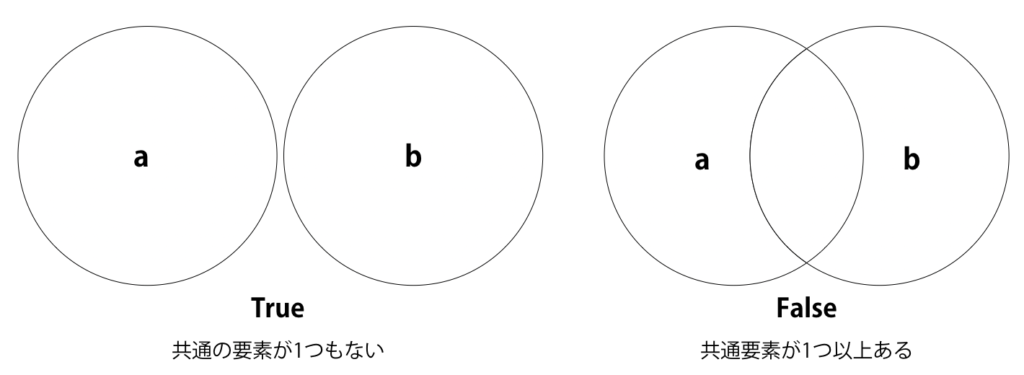
s1 = {1, 2, 3}
s2 = {4, 5, 6}
s3 = {3, 4, 5}
print(s1.isdisjoint(s2))
print(s1.isdisjoint(s3))
5.3. 部分集合の判定|<=演算子, issubset()
下図のようにaの要素がbの要素の一部分から成り立っている場合、aはbの部分集合といいます。
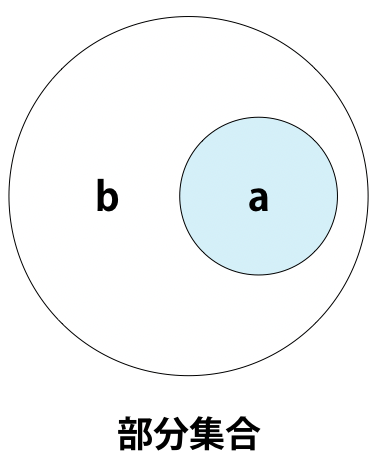
Pythonでは部分集合かどうかを判定するには2つの方法があります。
- <=演算子
- issubset()メソッド
s1 = {1, 2, 3}
s2 = {1, 2, 3, 4, 5, 6}
print(s1<=s2)
print(s1.issubset(s2))
<=演算子では、set同士の比較でなければエラーになりますが、issubset()メソッドは引数にリストやタプルなどのイテラブルを渡すことができるという点が異なります。
s1 = {1, 2, 3}
l1 = [1, 2, 3, 4, 5, 6]
print(s1.issubset(l1))
5.4. 上位集合の判定|>=演算子, issuperset()
下図のようにaの要素の中にbの要素が全て含まれている場合、aはbの上位集合といいます。
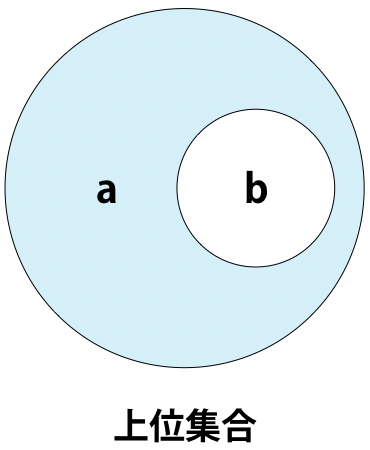
Pythonでは以下の2つの方法で、上位集合かどうかを判定することができます。
- >=演算子
- issuperset()メソッド
s1 = {1, 2, 3, 4, 5, 6}
s2 = {1, 2, 3}
print(s1>=s2)
print(s1.issuperset(s2))
s1 = {1, 2, 3, 4, 5, 6}
l1 = [1, 2, 3]
print(s1.issuperset(l1))
まとめ
Pythonにおいてsetの操作は、データ分析や科学技術計算の最初の一歩と言えるでしょう。
まずは、以下の点をしっかりとおさえておきましょう。
- setは重複した要素が存在しないミュータブル(変更可能)なオブジェクトである。
- setに要素の順番はない。
- frozenset()関数を使うとイミュータブル(変更不可能)なオブジェクトを作ることができる。
これらの点を抑えた上で、ここで解説している基本操作をしっかりとマスターしましょう。





コメント