ここでは確率を効率的に求められるようになるために覚えておきたい 12 個の公式をまとめています。必要なときに見返すようにして使って頂ければと思います。
それでは前置きは抜きにして、早速見ていきましょう。
0. 確率の基本用語と記号一覧
確率に関する公式を理解するには、最低限の用語と記号の意味を覚えておくことが必要です。そこで、まずはそれらを簡単におさらいしておきましょう。
- 確率 \(P(A)\)：ある試行において特定の事象が起こる可能性を数値化したもの
- 場合の数 \(n(A)\)：全事象の中で、ある特定の事象 A が起こりうる数
- 試行：同じ状態で何度も繰り返し観測することが可能であり、かつ、結果が偶然によって決まる行為
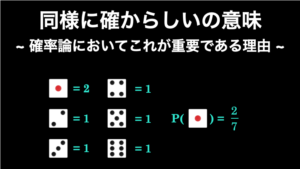
- 同様に確からしい：ある試行によって起こり得る事象のすべてが同じように起こる可能性があると期待できること
- 事象 \(A\) ~ \(Z\)：試行によって起こり得る出来事
- 全事象 \(U\) , \(\Omega\)：試行によって起こり得るすべての出来事
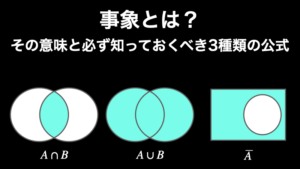
- 積事象 \(A \cap B\)：事象 A と B の両方が同時に起こる事象
- 和事象 \(A \cup B\)：事象 A または B が起こる事象（両方が同時に起こる事象を含む）
- 余事象 \(\overline{A}\) , \(A^c\)：事象 A に対して、A ではない事象すべて
それぞれの詳しい意味は、以下の 4 つの記事の中で解説しているので必要なときに読み返すようにしてください。
- 『場合の数とは？ ~ 樹形図の描き方と知っておくべき 2 つの法則 ~』
- 『同様に確からしいの意味 ~ 確率論においてこれが重要である理由 ~』
- 『事象とは？その意味と必ず知っておくべき 3 種類の公式』
- 『余事象とは？確率計算で必ず覚えておくべき重要な 1 つの法則』
それでは公式を見ていきましょう。
1. 確率を求める公式
まずは確率を求めるための公式を挙げていきます。
1.1. 基本の公式
確率において基本となる公式は…
- 計算方法
- 乗法定理
- 加法定理
- 和集合の法則
の 4 つです。そこでまずは、これらの公式を確認していきましょう。
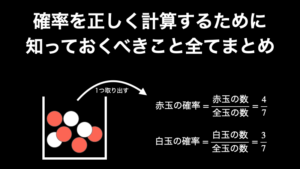
確率の計算方法
\[\begin{eqnarray}
P(A)
=
\frac{n(A)}{n(U)}
\end{eqnarray}\]
乗法定理
\[\begin{eqnarray}
P(A \cap B)
=
P(A)
\times
P(B)
\end{eqnarray}\]
加法定理
\[\begin{eqnarray}
P(A \cup B)
=
P(A)+P(B)-P(A\cap B)
\end{eqnarray}\]
和集合の法則
\[\begin{eqnarray}
P(A \cup B)
=
1-[P(\overline{A})\times P(\overline{B})]
\end{eqnarray}\]
解説や例題は、最初の 3 つについては『確率の求め方（計算方法）と最低限知っておくべき2つの公式』で、最後の 1 つについては『余事象とは？確率計算で必ず覚えておくべき重要な 1 つの法則』で見られますので、ぜひご確認ください。
1.2. 条件付き確率
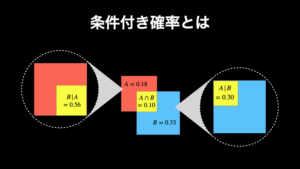
条件付き確率とは、事象 B が起こったという条件において事象 A が起こる確率のことです。これは以下の公式で求めることができます。
\[\begin{eqnarray}
P(A | B)
=
\dfrac{P(A \cap B)}{P(B)}
\end{eqnarray}\]
なお、この公式は、これ単体では確率としては、ほとんど役に立ちませんが、後述するベイズの定理を理解するためとしては非常に重要です。詳しくは『条件付き確率とは？ベイズの定理に繋がる重要な公式と練習問題』で解説しています。
1.3. ベイズの定理
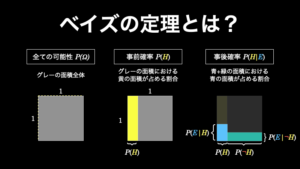
ベイズの定理は、条件付き確率の一種で、簡潔に言うと「ある結果 A が、ある原因 B によって引き起こされた確率（事後確率）」であり、その有用性から特に統計学の世界で大活躍している定理です。これは以下の公式で求められます。
\[\begin{eqnarray}
P(A | B)
=
\dfrac{P(B|A)P(A)}{P(B)}
\end{eqnarray}\]
詳しくは『ベイズの定理とは？証明や応用方法がよくわかる5つの例題』で解説しています。ベイズの定理は、確率論の世界で最も面白いものなので、ぜひご覧ください。
2. 場合の数を求める公式
ここでは確率計算において重要な「場合の数」の算出を楽にしてくれる「順列」と「組み合わせ」の公式を挙げていきます。
2.1. 順列の公式
順列とは「n 個の異なる物の中から r 個を取り出して順番に並べた時の、全事象の場合の数」のことです。
ここでは…
- 順列
- 円順列
- 重複順列（復元抽出の場合の順列）
- 要素が重複した順列
の 4 つを挙げています。
順列
基本的な順列です。公式は以下の通りです。
\[\begin{eqnarray}
{}_nP_r
=
\frac{n!}{(n-r)!}
\end{eqnarray}\]
詳しくは『順列とは？理解しておきたい4つの公式と計算方法』で解説しています。
円順列
円順列は、その名の通り要素を円形に並べる順列のことです。この場合は、以下の公式で求めることができます。
\[
(n-1)!
\]
詳しくは『円順列とは？解き方の公式と覚えるべき4つのパターン』で解説しています。
重複順列（復元抽出）
重複順列は、要素を 1 つ取り出すごとに状態を復元してから、次の要素を取り出す順列です。以下の方法で求められます。
\[
n^r
\]
詳しくは『重複順列の公式と解き方と押さえておくべき注意点』で解説しています。
要素重複順列
これは { A, A, B, B, B ,C } というように複数の同じ要素を含む集合から、要素を取り出す場合の順列です。集合の中に A が p 個、B が q 個、C が r 個あるとしたら、この場合の順列は以下の方法で求められます。
\[
\frac{n!}{p!q!r!}
\]
詳しくは「2.3. 同じ要素を含む順列｜順列とは」で解説しています。
2.2. 組み合わせの公式
組み合わせとは、「n 個の異なる要素の中から r 個を取り出す時の全事象の場合の数」のことです。順列との違いは、「並べ方が違っても要素が同じなら 1 通りである」と解釈する点です。
ここでは…
- 通常の組み合わせ
- 重複組み合わせ（復元抽出）
の場合 2 つの公式を挙げます。
組み合わせ
組み合わせは以下の方法で求めることができます。
\[\begin{eqnarray}
{}_nC_r
&=&
\frac{{}_nP_r}{r!}\\
&=&
\frac{n!}{r!(n-r)!}
\end{eqnarray}\]
詳しくは『組み合わせとは？絶対に知っておくべき 2 つの公式と計算のパターン』で解説しています。
重複組み合わせ（復元抽出）
重複組み合わせは、同じ要素を何回使っても良い場合（復元抽出の場合）の組み合わせのことです。これは以下の計算で求められます。
\[\begin{eqnarray}
{}_{n+r-1}C_r
\end{eqnarray}\]
「重複組み合わせ｜組み合わせとは」で例題がありますので、ぜひご確認ください。
3. まとめ
以上、確率を求めるために抑えておきたい公式まとめです。ぜひ役立てて頂ければと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント