重複順列の公式と解き方と押さえておくべき注意点

重複順列は、「同じ要素を繰り返し使っても良い順列」です。つまり、要素が重複しても良い順列ということですね。このページでは、この重複順列の具体例・公式・練習問題を解説します。特に、重複順列の練習問題は慣れないうちは混乱しがちなので、そうならないように意識すべきこともお伝えします。

なお通常の順列については『順列とは？抑えておきたい3つの公式と計算方法』で解説していますので、ぜひ併せてご覧ください。

それでは早速始めましょう。

1. 重複順列とは

繰り返しになりますが、重複順列とは、「同じ要素を繰り返し使っても良い順列」のことです。

たとえば 1, 2, 3 の 3 つの数字を使って 3 桁の数を作るとします。このとき同じ数字を繰り返し使っても良いこととします。この場合のあり得るパターンを樹形図で書き出してみると、全部で 27 通りあることがわかります。

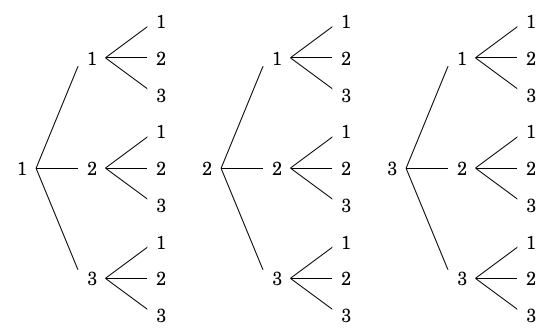
このように順列の中で、「同じ要素を重複して用いても良い場合の並び方」が重複順列です。

2. 重複順列の公式

n 個の要素の中から r 個取り出して重複順列を求める場合、その並べ方の数は以下の公式で求めることができます。

たとえば、上で見た 1, 2, 3 の 3 つの数字を使って 3 桁の数を作る重複順列は、次の通り計算できます。

\[3^3=27\]

1, 2, 3, 4 の 4 つの数字を使って 3 桁の数を作る場合の重複順列は、次の通りになります。

\[4^3=64\]

こうなる理由はとても簡単です。

通常の順列の場合は、{ 1, 2, 3, 4 } の 4 つの選択肢の中から最初に 1 を選んだとしたら、次は { 2, 3, 4 } という 3 つの選択肢の中から 2 桁目の数字を選び、最後に { 3, 4 } という 2 つの選択肢から 1 桁目の数字を選ばなければいけません。そのため、あり得る並べ方の数は 4 × 3 × 2 という階乗の計算で求められることになります。一方で重複順列では、選択肢の数は常に 4 つです。そのため 4 × 4 × 4 のべき乗計算で求められます。

3. 重複順列の例題

それでは理解を深めるために例題を解いておきましょう。

問題①

これは、A か B かの 2つの選択肢を 5 回行うことと同じなので、\(2^5=32\) 通りになります。一方の箱に最低 1 つはボールがなければいけない場合は、{ A:5, B:0 } と { A:0, B:5 } という 2 通りを引いて \(2^5-2=30\) 通りになります。

問題②

このような集合の問題も、重複順列で求めることができます。これは結局、1 つずつの数字を部分集合に入れるか・入れないかの 2 択を 3 回行うことと同じです。そのため、答えは \(2^3=8\) 通りになります。実際に書き出してみると、以下の通りです。空集合が入っている点に注目しましょう。

{ }, {1}, {2}, {3}, {1, 2}, {1,3}, {2, 3}, {1, 2, 3}

問題③

これも、A, B, C, D という 4 択を 5 回繰り返すだけなので \(4^5=1024\) 通りになります。

4. まとめ

以上が重複順列です。

重複順列は、選択肢が n 個あるものを r 回行うというだけのものなので、そのパターン数は \(n^r\) で求められます。問題文に惑わされず、選択肢が何個で、それを何回行うのかを把握できさえすれば、とても簡単です。