-

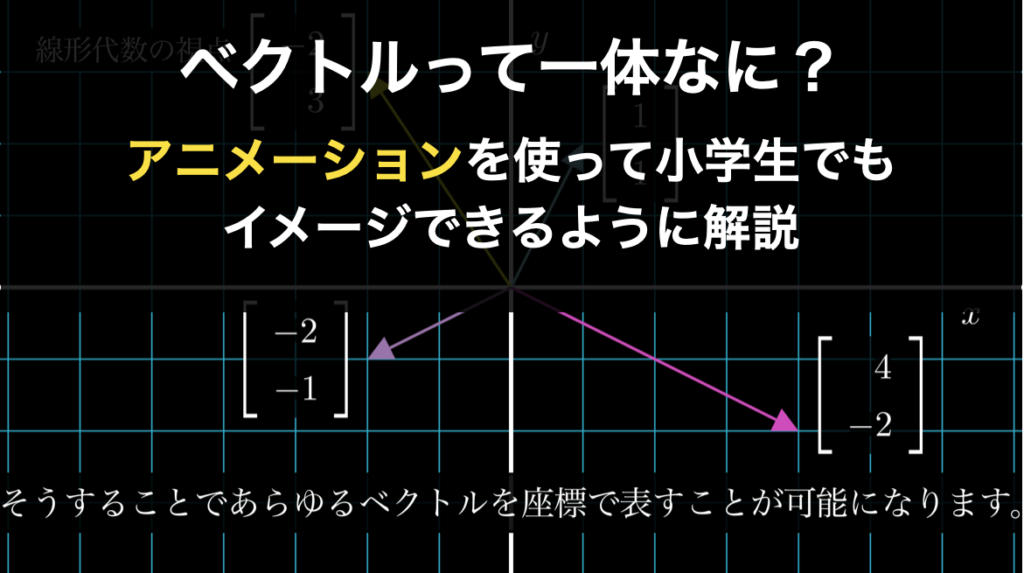
ベクトルとは?誰でも理解できるように簡単に解説
ベクトルとは、一般的には「大きさと向きをもつ量」であり「矢印で表すことのできる量」と説明されます。 ただし、この説明は物理学的な視点に立ったときの解釈です。実際は、ベクトルはさまざまな分野で異なった使い方をされている概念であるため、その定... -

2×2, 3×3, 4×4 の行列式の計算方法[練習問題付き]
このページでは、2次行列式、3次行列式、4次行列式のそれぞれの行列式の計算方法と、その覚え方を解説しています。さらに理解を深めるための練習問題も用意しています。お役に立てば嬉しく思います。 それでは見ていきましょう。 なお、ここで解説してい... -

余因子行列で逆行列の公式を求める方法と証明について解説
余因子行列を使うと、有名な逆行列の公式を求めることができます。実際に逆行列の公式を使って逆行列を求めることはほとんどありませんが、逆行列の公式について考えることで、行列式や余因子行列についてより深く理解できるようになります。そして、これ... -

余因子による行列式の展開とは?~アニメーションですぐわかる解説~
行列式の展開とは、簡単に言うと「高次の行列式を、次元が一つ下の行列式(小行列式)の和で表すこと」です。そして、小行列式を表すために「余因子」というものを使います。これらについて理解しておくことで、有名な逆行列の公式をはじめとした様々な公... -

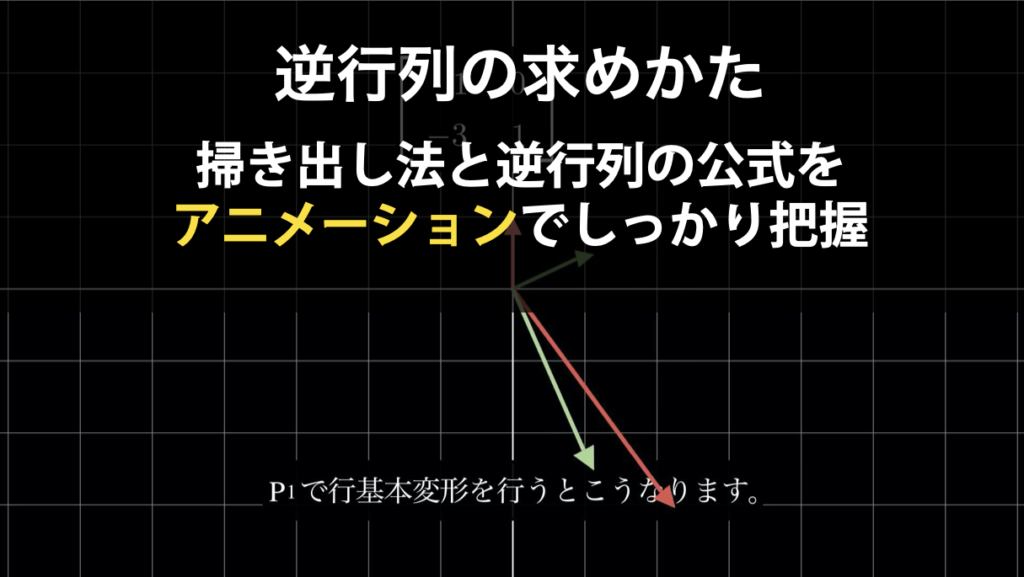
逆行列の求め方~掃き出し法と逆行列の公式の2つの方法の徹底解説~
当ページでは逆行列の求め方について、以下の2つの方法を解説します。 掃き出し法逆行列の公式 先にお伝えすると、逆行列は掃き出し法で求めるのが一般的です。 一方で、逆行列の公式は、手計算において実際に使うことはほとんどありません。しかし、逆行... -

連立方程式を行列で解く方法|行の基本変形と掃き出し法とは
行列で連立方程式の解を求めるのは、最も基本的な行列の使い方の一つです。とてもシンプルなものですが、行列を扱う上でなくてはならない技術です。 また、普通の解き方では、未知数が何十何百もあるような連立方程式に対応することはほとんど不可能です。... -

ベクトルの引き算の求め方と計算方法の初心者のための解説
ベクトルの引き算は、幾何学的には、反転したベクトルとの和で求めることができます。成分表示においては、単純にそれぞれの座標ごとに引き算をすることで求めることができます。 このベクトルの引き算を使いこなせるようにあると、例えば、速度 \( \vec{a... -

NumPyでテンソル積を取得するtensordot()関数の使い方
Numpyのtensordot()関数は、2つのテンソル(3次元配列)からテンソル積を求める関数です。 2つのテンソルa とb を渡して、第三引数に (aの次元軸, bの次元軸)をタプルで渡すと、a とb の指定の次元軸の要素の積の和を求めます。第三引数に1つの整数N だけを... -

NumPyで外積を取得する方法 – numpy.crossの使い方
【1. ベクトルの外積とは】 まずはベクトルの外積について軽くおさらいしておきましょう。これは2つのベクトルが作る平行四辺形に対して垂直な方向に伸びるベクトルのことです。そして、ベクトルの外積の長さは、平行四辺形の面積と等しくなります。以下... -

NumPy配列の条件を満たす要素の確認や置換・カウントの方法まとめ
NumPyの配列から条件に合う要素を探索して操作するための主な関数やメソッドには以下があります。 これら以外にも使用可能な関数やメソッドはありますが、基本的にはこれらを抑えておけば十分です。もし、これら以外が気になるとしても、このページからの... -

多次元配列から任意の要素を取得するnumpy.choose()の使い方
numpy.choose()は、インダイスの配列によって、多次元配列から要素を取得する際に使います。これを使わない場合と比べて、かなり自由に任意の値を取得することが可能になります。 解説が多少長くなっていますので、まずサンプルコードを先に見てからの方が... -

NumPyで条件に合う要素のインダイスを取得するargwhere()の使い方
NumPyのargwhere()関数は、① 0以外の要素のインダイスを要素ごとに取得します。または、② 指定の条件に合致する要素のインダイスを要素ごとに取得します。 ①と同じ働きをする関数には、ほかにnumpy.nonzero()もあります。しかし、こちらは0以外の要素のイ...