-

逆行列とは?誰でも理解できるようにわかりやすく解説
逆行列とは、簡単に言うと、ある行列で線形変換した空間を元に戻す行列であり、その働きから行列における割り算のようなものと説明されることもあります。 線形代数において中心的かつ重要な概念であり、逆行列がなければできないような計算や処理も多々あ... -

行列式とは?誰でも理解できるようにわかりやすく解説
行列式は、線形代数において必ずお世話になる計算式であり、様々なことを表す非常に便利な指標です。しかし、教科書を見てみると、「線型変換によって空間の体積要素が何倍に変わるかという概念を抽象化したもの」というように定義されており、なかなか字... -

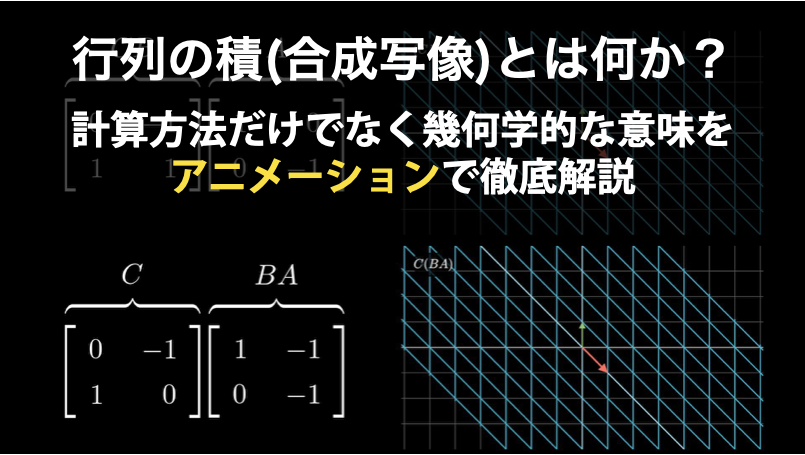
行列の積(掛け算)とは何か?わかりやすく解説
行列の積(掛け算)とは、簡単に言うと、空間を異なる複数の行列で続けて線形変換したときに、空間が最終的にどう変化するのかの計算です。いきなりですが、まずは以下のアニメーションをご覧ください。行列の積とは何であるかが一目でわかります。 このよう... -

線形変換とは?誰でも必ず理解できるようにアニメーションで解説
線形変換(線型写像)とは、簡単に表現すると「行列によって空間(線形空間)を変形させること」です。具体的には、以下に用意した線形変換のアニメーションをご覧ください。これだけで線形変換がどういうものであるかが一目でわかります。 いかがでしょう... -

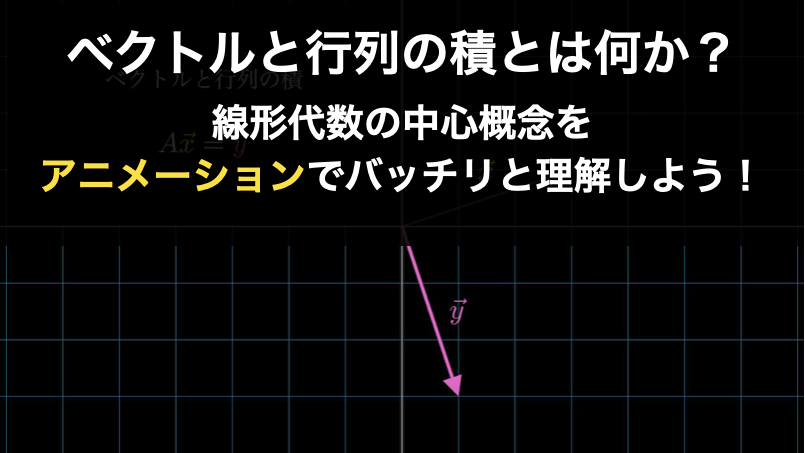
行列とベクトルの積とは何か?わかりやすく解説
ベクトルと行列の積は、簡単に言うと「ベクトルを行列に入力して新たなベクトルを出力すること」です。これは、線形代数のさまざまな概念を理解する上で中核となるものです。 当ページでは、このベクトルと行列の積について以下の順番で解説していきます。... -

ベクトルの一次独立(線型独立)とは?アニメーションで一目で理解
ベクトルの一次独立(「線型独立」ともいう)とは、一言でいうと「空間における基底ベクトルがすべてゼロベクトルではなく、平行関係にない状態」のことです。 このページでは、これが一体何を表しているのかを、誰でも絶対にわかるように、アニメーション... -

一次結合(線型結合)とは何か?アニメーションで一目で理解
一次結合(線型結合)は、線形代数において重要な概念の一つであり、簡単に言えば「ベクトルのスカラー倍と足し算によって、任意のベクトルを表すこと」です。たとえば、2次元ベクトルで言うと \(x\vec{v}+y\vec{w}\) のことです。 このページでは、この線... -

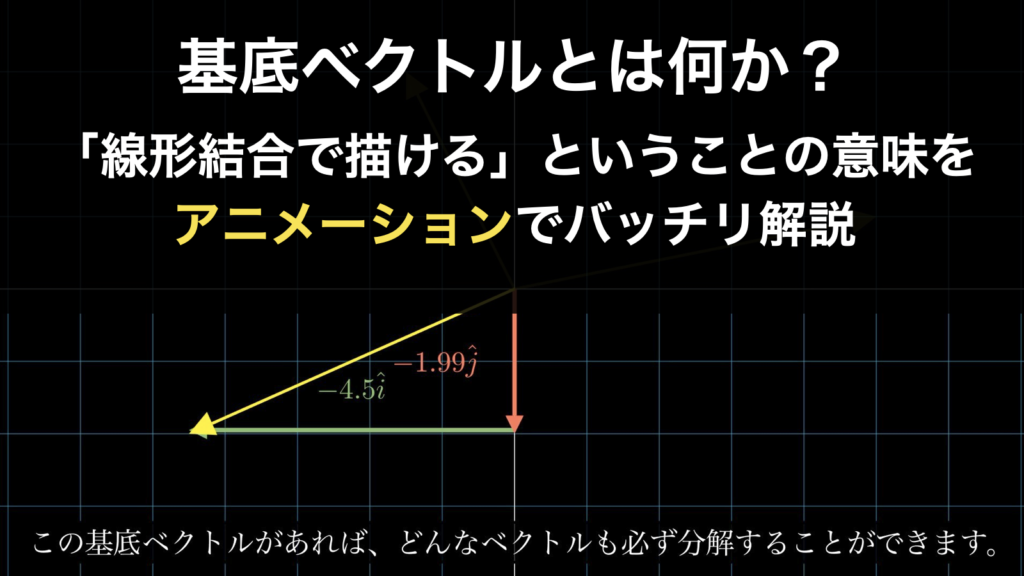
基底ベクトルとは何か?アニメーションで一目で理解
基底ベクトルとは、簡潔に言うなら「空間上のあらゆるベクトルを v=xa+yb のかたちで表すことを可能にするベクトル a, b の組み合わせ」のことです。言葉だけでも理解できないことはないですが、そこからこの意味するところを具体的にイメージするのは難し... -

ベクトルの分解とは何かを誰でもわかるように解説
ベクトルの分解とは、簡単に言うと「任意のベクトルを、基準となる2本のベクトルの掛け算と和で表すこと」です。 こう聞くと、「なぜわざわざそんな面倒なことをするのか?」と疑問に思うかもしれません。しかしベクトルの分解は線形代数において非常に重... -

ベクトルの掛け算とは何か?意味と計算方法をわかりやすく解説
ベクトルの掛け算とは簡単に言うと、「ベクトルの向きはそのままで、長さを伸ばしたり縮めたりすること」です。 これはベクトルの和と並んで、線形代数において基礎となる重要な計算です。なぜなら、あらゆるものごとを線形代数的に分析するための土台(「... -

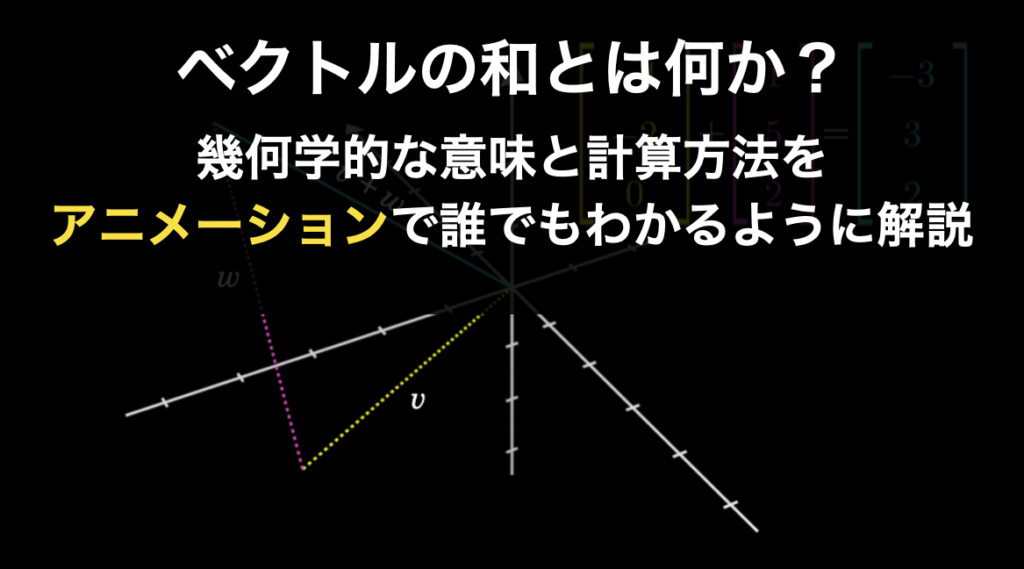
ベクトルの足し算(和)の計算方法をわかりやすく解説
ベクトルの足し算(和)は、幾何学的には「二つのベクトルを継ぎ足したときの最終的な座標に対して、原点から伸びる新しいベクトル」です。数学的には「二つのベクトルの座標を成分ごとに足し合わせたもの」です。 これはベクトルの掛け算と並んで、「線形... -

ベクトルの座標とは何か?アニメーションで一目で理解
ベクトルの座標とは、あるベクトルの長さと向きを数字の組み合わせで表すための概念です。 少しおさらいですが、前回の記事『ベクトルとは一体なに?その意味と定義が深く理解できる解説』で解説したように、ベクトルとは長さと向きをもつ矢印です。しかし...