-

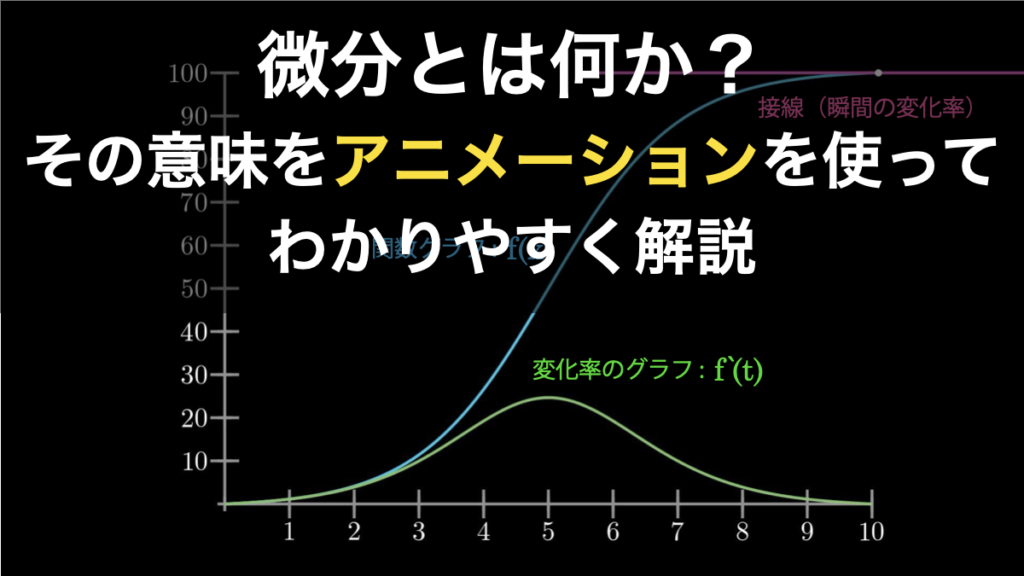
微分とは何か?わかりやすくイメージで解説
微分とは、結論から言うと「瞬間の変化率」のことであり、視覚的には「ある関数のある地点における接線の傾き」のことです。また概念的には、微分は「ある複雑な事象の全体を非常に細かいパーツに分解して、分析すること」を意味します。 そして実務におい... -

線形代数とは?初心者にもわかりやすい解説
「線形代数を簡単に理解できるようになりたい…」。そう思ったことはないでしょうか。当ページはまさにそのような人のためのものです。ここでは線形代数の基礎のすべてを、誰でもすぐに、そして直感的に理解できるように、文章だけでなく、以下のような幾何... -

ジョルダン標準形とは?意義と求め方を具体的に解説
ジョルダン標準形は、対角化できない行列を擬似的に対角化(準対角化)する手法です。これによって対角化不可能な行列でも、べき乗の計算がやりやすくなります。当ページでは、このジョルダン標準形の意義や求め方を具体的に解説していきます。 【1. ジョ... -

行列の対角化とは?意味と方法と使い方[練習問題付き]
行列の対角化とは、ある行列の固有値を成分とした対角行列を作ることを意味します。 これはシンプルですが強力なツールであり、経済学から統計学、工学、物理学に到る様々な分野で、主に漸化式や微分方程式を効率よく解くために使われています。 そこで、... -

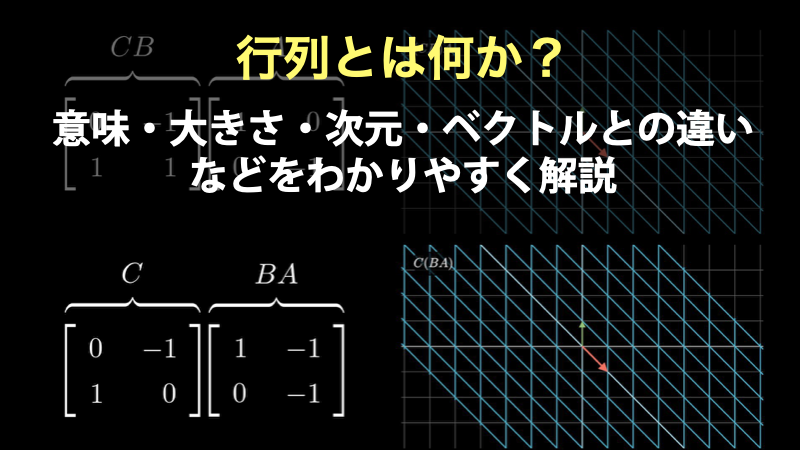
線形代数のための行列の基礎~意味や大きさ・次元・ベクトルとの違い
行列は線形代数において欠かせないものであり、さまざまな便利な性質をもつツールです。その便利さから、連立方程式の計算や、空間の線形変換、統計学の最小二乗法など、さまざまな分野で中心的な役割を担っています。 ここでは、この重要な概念である行列... -

行列の基本変形とは?その幾何学的意味や逆行列との関係の解説
行列の基本変形は、「①ある行をスカラー倍する」「②ある行と別の行を入れ替える」「③スカラー倍した行を別の行に足す」という3つの操作のことです。これは連立方程式を行列を使って解いたり、逆行列を求める際に使う基本的なテクニックです。 当ページで... -

行列の階数(ランク)とは何か?意味や求め方をわかりやすく解説
行列の階数(ランク)とは、「その行列で線形変換を行ったときに、空間が何次元になるのか」を示すものです。 これにはどういう意義があるのでしょうか? 『正則行列とは何かがアニメーションで驚くほどよくわかる解説』でお伝えした通り、ある行列が正則... -

正則行列とは?誰でも理解できるようにわかりやすく解説
正則行列(「非特異行列」または「可逆行列」ともいう)とは、逆行列をもつ正方行列のことです。当ページでは、この正則行列について、誰でも直感的に、かつ確実に理解できるようにアニメーションを用いながら、わかりやすく解説していきます。 正則行列と... -

固有値と固有ベクトルとは何か?幾何学的意味と計算方法の解説
行列の固有値と固有ベクトルは、線形代数において重要な概念であり、数学だけでなく、統計学や経済学、物理学、コンピューター・サイエンスなど様々な分野において不可欠な概念です。 あまりにも多くの分野において中核を担っている概念であるため、これを... -

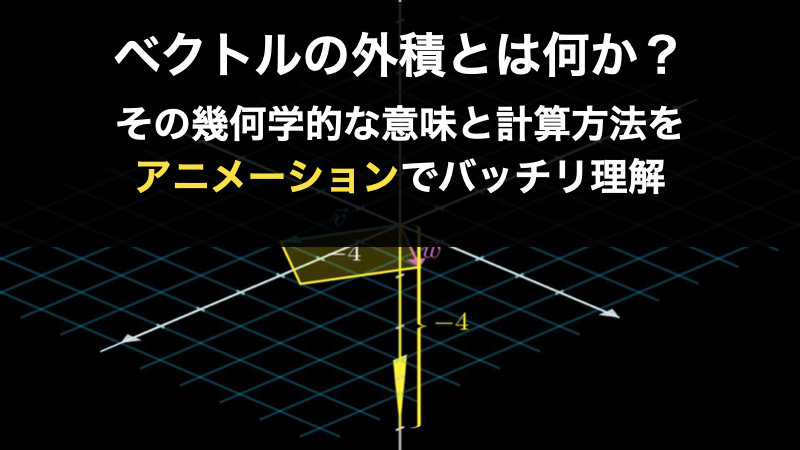
ベクトルの外積とは何?意味と計算方法をわかりやすく解説
ベクトルの外積とは、「2本のベクトルが作る平行四辺形に対して、垂直な方向に働く新しいベクトル」のことです。そして、ベクトル \(\vec{v}\) と \(\vec{w}\) があるとき、外積は \(\vec{v}\times \vec{w}\) と表すので、「クロス積」とも言います。 この... -

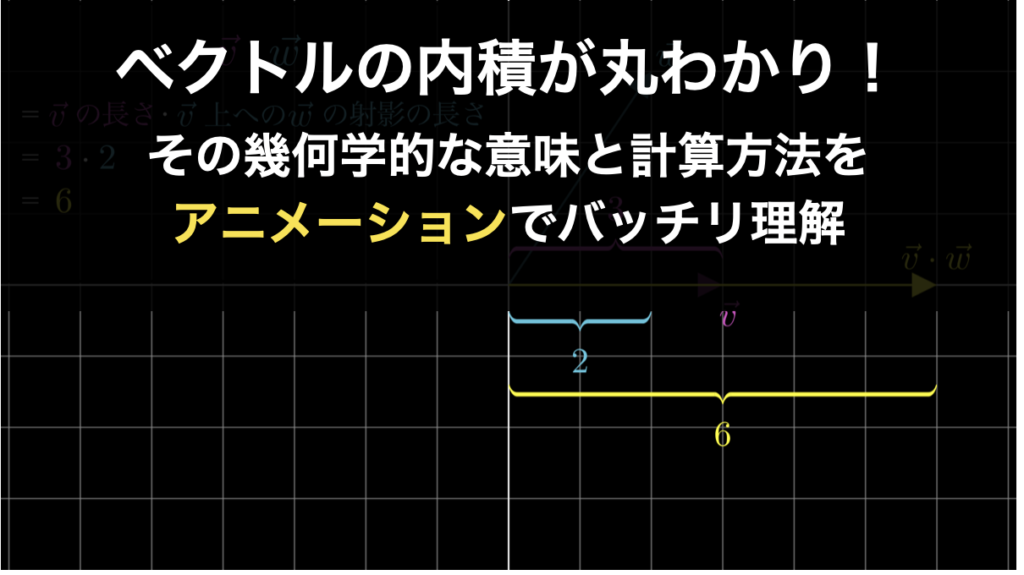
ベクトルの内積とは?誰でも理解できるようにわかりやすく解説
ベクトルの内積は、一般的に、「一方のベクトル \(\vec{v}\) に対して垂直な光を当てたときに、ベクトル \(\vec{v}\) 上にできるベクトル \(\vec{w}\) の射影の長さと、元のベクトル\(\vec{v}\) の長さとの積」と説明されます。 しかし、これだけではベク... -

行列の計算方法のまとめ~線形代数で特に重要なもの3つを徹底理解!~
行列は空間を変換する写像(=関数)であり、線形変換においてなくてはならぬツールです。ここでは、この行列について、線形代数で非常に重要な以下の3つの計算方法を解説していきます。 ベクトルと行列の積正方行列と正方行列の積非正方行列と正方行列の...