MENU
  1. ホーム
  2. AIプログラミング
  3. NumPy
  4. NumPyのdiff関数の使い方 – 第n階差数列を取得する方法

NumPyのdiff関数の使い方 – 第n階差数列を取得する方法

NumPy
2020年9月3日

NumPyのdiff()は、渡した配列の指定の軸方向の第n階差数列を返す関数です。

似たような関数に、numpy.ediff1d()もあります。diff()とediff1d()の最大の違いは、多次元配列を渡した場合の処理にあります。前者は元の多次元配列と同じshapeの階差数列を戻しますが、後者は1次元配列の階差数列を戻します。

このページでは、この2つの関数についてわかりやすく解説します。実際のコードを見ながら確認していきましょう。

NumPy配列の差分を取得する操作まとめ
配列の差分の操作に関しては、『NumPyの差分を取得する関数とメソッドまとめ』ですべて簡潔にまとめています。ぜひご確認ください。

目次

1. numpy.diffの使い方

まずは書き方を見ていきましょう。

numpy.diff関数

書き方:

np.diff(a, n=1, axis=-1, prepend=<no value>, append=<no value>)

パラメータ: 

引数 　 型  解説
a　　 array_like　　 配列を渡します。
n*　　 int　　　 第n階差を指定します。デフォルトでは第1階差数列を生成します。
axis* int　　 多次元配列の場合で、どの軸方向に階差数列を生成するかを指定します。デフォルトは-1です。
prepend, append*　 array_like　 階差数列を求める際に配列aの前方(prepend)、または後方(append)に指定の値を加えます。スカラーの値を指定した時は、要素数の分だけ延長されます。それ以外の場合は、指定の軸以外のshapeが一致している必要があります。
* はオプション引数であることを示します。

戻り値: 

階差数列の配列：
第n階差数列を返します。戻り値の配列のshapeは、次元数がnより小さい場合、指定の軸以外は引数に渡した配列と同じになります。戻り値の配列のデータ型は元の配列と同じになります。しかし、元の配列のデータ型がdatetime64の場合、戻り値の配列のデータ型はtimedelta64になります。

一緒に確認したい関数:

  • gradient
  • ediff1d
  • cumsum: 配列の要素の累積合計を取得

それではサンプルコードを見ながら使い方を確認していきましょう。

階差数列を取得

numpy.diffは、渡した配列の階差数列を生成します。

まずは以下の1次元配列を例に見てみましょう。

In [1]:
import numpy as np
arr = np.array([1, 2, 3, 5, 8, 13, 21, 34, 55, 89])
arr
Out[1]:
array([ 1,  2,  3,  5,  8, 13, 21, 34, 55, 89])

この配列をnumpy.diffに渡すと次のように、各要素間の差が返ってきています。

In [2]:
#  要素間の離散差
np.diff(arr)
Out[2]:
array([ 1,  1,  2,  3,  5,  8, 13, 21, 34])

なお、numpy.diffは、渡した配列の階差数列を生成するために以下のような処理を繰り返し行なっています。

In [3]:
#  階差数列の計算式
out = np.array([arr[1]-arr[0], arr[2]-arr[1], arr[3]-arr[2], arr[4]-arr[3]])
out
Out[3]:
array([1, 1, 2, 3])

第n階差数列を取得

オプション引数nを指定すると、何番目の階差数列を生成するかを指定することができます。

以下のコードをご覧ください。

In [4]:
#  第２階差
print(np.diff(arr, n=2))
#  第３階差
print(np.diff(arr, n=3))
#  第４階差
print(np.diff(arr, n=4))

[ 0  1  1  2  3  5  8 13]
[1 0 1 1 2 3 5]
[-1  1  0  1  1  2]

これらはそれぞれ以下の計算式を繰り返すことで生成されています。

In [5]:
#  第２階差数列の計算式
sec = np.array([arr[2]-2*arr[1]+arr[0], arr[3]-2*arr[2]+arr[1]])
print(sec)
#  第３階差数列の計算式
thr = np.array([arr[3]-3*arr[2]+3*arr[1]-arr[0], arr[4]-3*arr[3]+3*arr[2]-arr[1]])
print(thr)
#  第４階差数列の計算式
forth = np.array([arr[4]-4*arr[3]+6*arr[2]-4*arr[1]+arr[0], \
                  arr[5]-4*arr[4]+6*arr[3]-4*arr[2]+arr[1]]) 
print(forth)

[0 1]
[1 0]
[-1  1]

次元軸を指定して階差数列を取得

numpy.diff()に多次元配列を渡す場合はオプション引数axisで、階差数列を求める軸方向を指定します。なお、デフォルトはaxis=-1です。

以下の2次元配列を例に見ていきましょう。

In [6]:
#  2次元配列を生成
arr = np.array([1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 238]).reshape(3, 4)
arr
Out[6]:
array([[  1,   2,   3,   5],
       [  8,  13,  21,  34],
       [ 55,  89, 144, 238]])

デフォルトのaxis=-1では、以下のコードのように横方向の要素同士の階差数列を生成します。

In [7]:
#  デフォルトはaxis=-1（列方向の差分を計算)
np.diff(arr)
Out[7]:
array([[ 1,  1,  2],
       [ 5,  8, 13],
       [34, 55, 94]])

縦軸方向の階差数列を生成したい場合は、2次元配列はaxis=0で2次元軸を指定します。

以下のコードをご覧ください。

In [8]:
#  axis=0で行方向の差分を計算
np.diff(arr, axis=0)
Out[8]:
array([[  7,  11,  18,  29],
       [ 47,  76, 123, 204]])

なお、出力結果の配列を1次元配列で受け取りたい場合は、後述するnumpy.ediff1d()を使います。

配列の前方に指定の値を追加

オプション引数prependを使うと、指定の軸の前方に指定の値を加えた上で階差数列を生成します。

これを指定する時は、軸方向以外のshapeが一致している必要があります。例えば、shape(N, M)の2次元配列に対して使う場合、行(axis=0)の前方に加える配列はshape(○, M)に、列(axis=1)の前方に加える配列はshape(N, ○)になっている必要があります。

以下の2次元配列を例に見ていきましょう。

In [9]:
arr = np.array([1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 238]).reshape(3, 4)
print(arr)

[[  1   2   3   5]
 [  8  13  21  34]
 [ 55  89 144 238]]

以下のコードでは、この配列の行の先頭に指定の要素を追加した上で階差数列を生成しています。

In [10]:
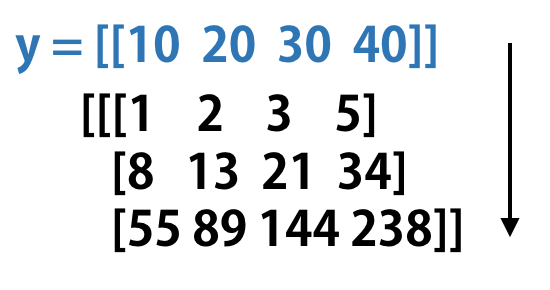
#  prepend(axis=0)
y = np.array([[10, 20, 30, 40]])
np.diff(arr, axis=0, prepend=y)
Out[10]:
array([[ -9, -18, -27, -35],
       [  7,  11,  18,  29],
       [ 47,  76, 123, 204]])

なお、加える値が全て同一の場合は、以下のようにshapeは気にせずに、スカラーを指定するだけで構いません、

In [11]:
np.diff(arr, axis=0, prepend=10)
Out[11]:
array([[ -9,  -8,  -7,  -5],
       [  7,  11,  18,  29],
       [ 47,  76, 123, 204]])

以下のコードでは、列の先頭に指定の要素を追加した上で階差数列を生成しています。

In [12]:
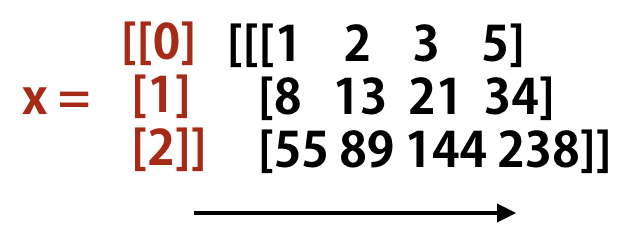
#  prepend(axis=1)
x = np.array([[0], [1], [2]])
np.diff(arr, axis=1, prepend=x)
Out[12]:
array([[ 1,  1,  1,  2],
       [ 7,  5,  8, 13],
       [53, 34, 55, 94]])

配列の後方に指定の値を追加

オプション引数appendは、配列の指定の軸の後方に、指定の値を追加した上で階差数列を求めたい時に使います。

以下のコードでは、行の最後に指定の値を追加した上で階差数列を生成しています。

In [13]:
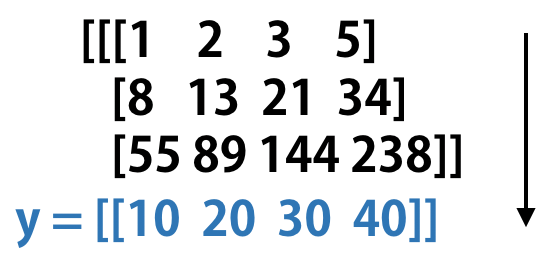
#  append(axis=0)
y = np.array([[10, 20, 30, 40]])
np.diff(arr, axis=0, append=y)
Out[13]:
array([[   7,   11,   18,   29],
       [  47,   76,  123,  204],
       [ -45,  -69, -114, -198]])

次に以下のコードでは、列の最後に指定の要素を追加した上で階差数列を生成しています。

In [14]:
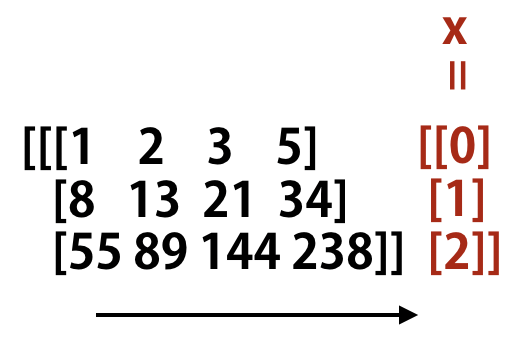
#  append(axis=1)
np.diff(arr, axis=1, append=x)
Out[14]:
array([[   1,    1,    2,   -5],
       [   5,    8,   13,  -33],
       [  34,   55,   94, -236]])

Note: ブール値の配列を扱う際の注意点

補足ですが、要素がブール値の配列に対して、numpy.diff()を実行する際には注意点があります。

以下のように、データ型がunit8型の場合は計算に支障が出ます。

In [1]:
u8_arr = np.array([True, False], dtype=np.uint8)
u8_arr
Out[1]:
array([1, 0], dtype=uint8)
In [2]:
np.diff(u8_arr)
Out[2]:
array([255], dtype=uint8)
In [3]:
u8_arr[1]-u8_arr[0]
Out[3]:
255

これを回避したい場合は、numpy.astypeで、配列のデータ型をより大きな整数型のものに変換してから、numpy.diff()に渡します。

In [4]:
i16_arr = u8_arr.astype(np.int16)
np.diff(i16_arr)
Out[4]:
array([-1], dtype=int16)

2. numpy.ediff1dの使い方

続いてnumpy.ediff1d()関数についても確認しておきましょう。この関数は、多次元配列を渡した場合でも、1次元配列で階差数列を戻す関数です。

以下で書式を確認しましょう。

numpy.ediff1d関数

書き方:

np.ediff1d(a, to_end=None, to_begin=None)

パラメーター:

引数 　 型  解説
a　　 array_like　　 配列を渡します。
to_end*　　 array_like　　　 配列の要素の一番後ろに付け加える数値を指定します。
to_begin* array_like　 配列の要素の一番前に付け加える数値を指定します。
* はオプション引数であることを示します。 

戻り値：

階差数列の1次元配列：
階差数列を1次元配列で返します。

一緒に確認したい関数:

  • diff, gradient

1次元配列の階差数列を取得

numpy.diff()を見てきた後なら、numpy.ediff1d()を使いこなすのは簡単です。この関数は、多次元配列を渡した場合でも、階差数列を1次元で返します。

以下の配列を例に確認しましょう。

In [1]:
import numpy as np
rng = np.random.default_rng()
a = rng.integers(0, 11, (2, 5))
a
Out[1]:
array([[9, 2, 8, 1, 7],
       [0, 2, 6, 9, 4]])

階差数列の前後に任意の値を追加

この配列a をnumpy.ediff1d()に渡すと、階差数列数列を1次元配列で戻します。

In [2]:
# 階差数列を1次元配列で戻す
np.ediff1d(a)
Out[2]:
array([-7,  6, -7,  6, -7,  2,  4,  3, -5])

オプション引数 to_begin で階差数列の先頭に値を追加することができます。

オプション引数 to_end では階差数列の最後に値を追加します。

In [4]:
# 一番後ろに値を追加
np.ediff1d(a, to_end= 0)
Out[4]:
array([-7,  6, -7,  6, -7,  2,  4,  3, -5,  0])

3. まとめ

以上が、NumPy配列の階差数列を取得するnumpy.diif()とnumpy.ediff1d()の使い方です。うまく使い分けられると良いでしょう。

Python初心者におすすめのプログラミングスクール

「未経験からでもPythonを学べるプログラミングスクールを探しているけど、色々ありすぎてわからない」なら、次の３つのプログラミングスクールから選んでおけば間違いはありません。

Aidemy Premium：全くの初心者ができるだけ効率よく短期間で実務的に活躍できるAI人材になることを目的とした講座。キャリアカウンセリングや転職エージェントの紹介などの転職支援も充実しており、受講者の転職成功率が高い。

AIジョブカレ：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。

データミックス：プログラミング経験者のビジネスマンが、更なるキャリアアップのためにデータの処理方法を学んでデータサイエンティストになるための講座。転職だけでなく起業やフリーランスとして独立する人も多い。Python初心者用の対策講座もある。

特に、あなたが以下のような目標を持っているなら、この中から選んでおけば間違いはないでしょう。

・未経験からPythonエンジニアとして就職・転職したい
・AIエンジニアやデータサイエンティストとしてキャリアアップしたい
・起業やフリーランスを視野に入れたい

理由は「Python初心者のためのおすすめプログラミングスクール3選」で解説しています。



NumPy
よかったらシェアしてね！
  • URLをコピーしました！
  • URLをコピーしました！

この記事を書いた人

ひろのアバター ひろ

関連記事

コメント

コメントする

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。

目次
閉じる