場合の数とは？ 誰でも理解できるようにわかりやすく解説

場合の数は、確率について学ぶときに必ず出てくる言葉で、「ある特定の状況において起こりうる事象の数」を意味します。しかし「場合の数」という言い回しは直感的には意味が通らないため、多くの人がいまいち理解できずにいます。

そこで、このページではまず「場合の数とは何か」という点について、誰でも理解できるように解説します。そして、なぜ、このように誰も直感的に理解できないような言い回しになってしまったのかについても解説します。その後、場合の数を正確に求めるために、最低限知っておくべきテクニックもお伝えします。

それでは早速見ていきましょう。

1. 場合の数の意味

「場合の数」とは、「ある特定の状況で起こりうると考えられる事象の数」のことです。もっと簡単に言うと「場合の数」は「事象の数」と同じ意味です。

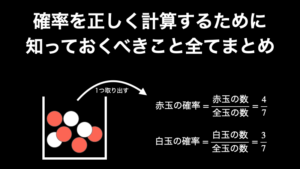
たとえば、吉・平・凶のおみくじが 1 つずつ入っている箱から 1 回引くとしたら、起こりうる事象（場合）は以下の 3 つです。

• 吉を引くという事象：（吉を引く場合）
• 平を引くという事象：（平を引く場合）
• 凶を引くという事象：（凶を引く場合）

このように、このときの「事象の数」は 3 つです。これが「場合の数」です。言葉の問題に煩わされたくない方は、とにかく「場合の数」と聞いたら「（起こりうる）事象の数」と頭の中で変換するようにしてください。それだけで「場合の数」という言葉のわかりづらさは、かなり解消することができます。

以上が「場合の数」の意味です。

2. 場合の数を求める方法

さて、ここからは場合の数のかぞえ方を学んでいきましょう。これは基本的には全て書き出すということを行います。

たとえば機内食で、まずメニューをビーフ・チキンの 2 つから、ドリンクをコーヒー・紅茶・水の 3 つから 1 つずつ選ぶとします。このとき「場合の数」はいくつになるでしょうか。

実際にあり得る組み合わせをすべて書き出すと以下の通りになります。

ビーフ・コーヒー,　ビーフ・紅茶,　ビーフ・水
チキン・コーヒー,　チキン・紅茶,　チキン・水

つまり、このときの「場合の数」は 6 個です。

このように場合の数は、基本的に考えられるすべての組み合わせを書き出すことで導き出します。しかし、いちいち書き出すのは、やはり面倒です。そこで場合の数をかぞえるための便利なテクニックがあります。それが以下の 3 つです。

• 樹形図
• 積の法則
• 和の法則

この 3 つのテクニックを使いこなせるようになれば、さまざまな「場合の数」を求められるようになりますので、しっかり押さえておきましょう。1 つずつ解説します。

樹形図の描き方

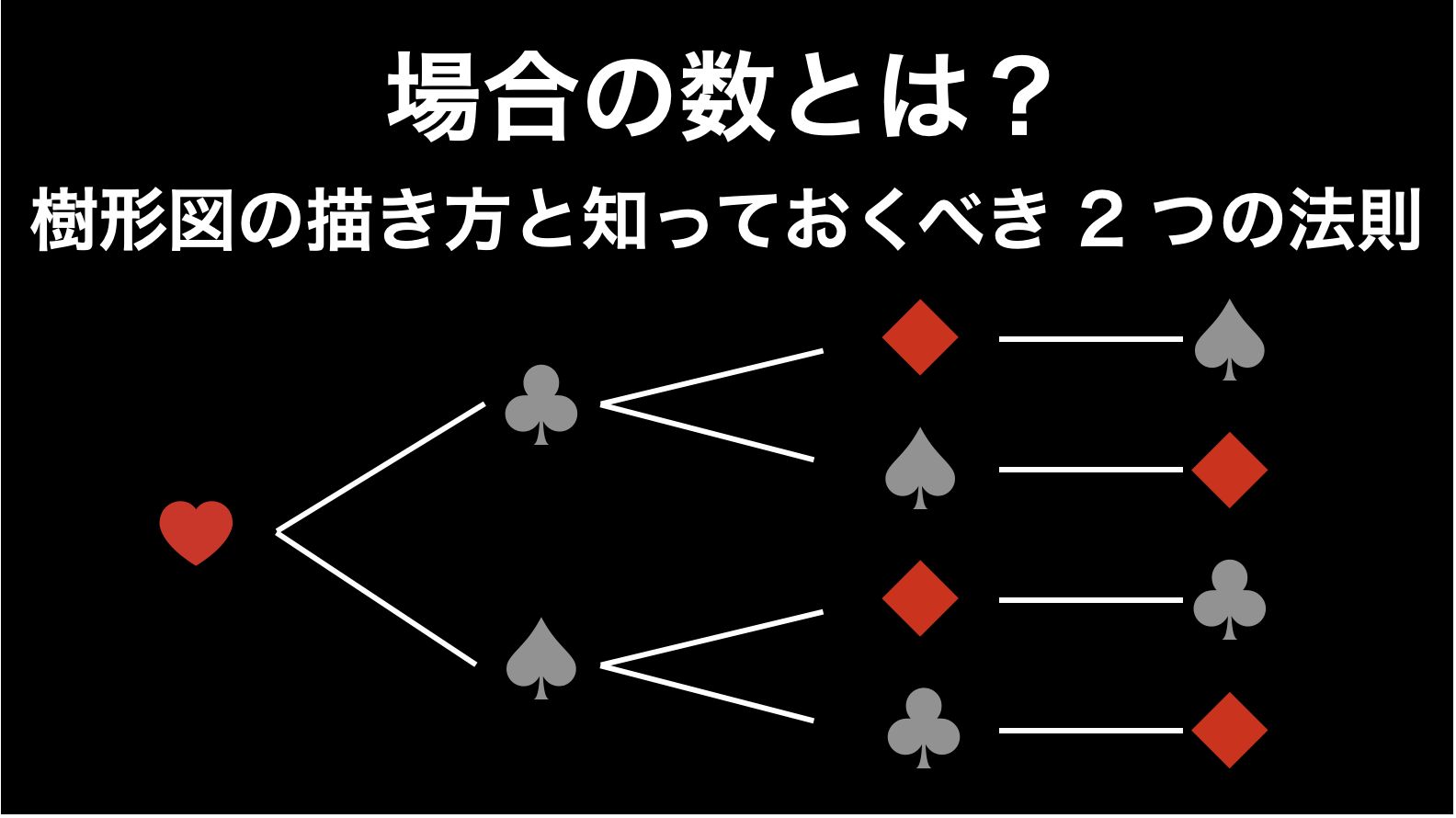
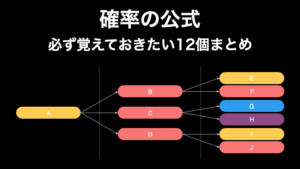
まず樹形図は、以下のようなツリーの形をした枝分かれ図のことです。これは確率論で「場合の数」を求めるときによく使われます。

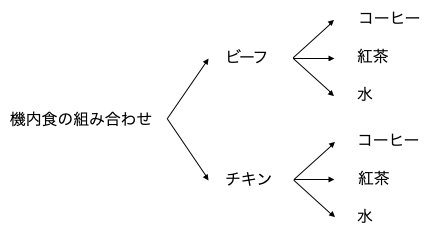
ご覧のように、樹形図を使うと、全ての組み合わせを簡単に書き出すことができますし、書き漏れが起こる心配もとても小さくなります。この例では組み合わせが合計 6 個しかありませんが、数が増えれば増えるほど、樹形図の有り難みが増していきます。

積の法則

簡単な問題であればいちいち樹形図を描かなくても、組み合わせの数を計算で求めることができます。その 1 つが積の法則です。これは選択肢の数を掛け合わせるというものです。

引き続き機内食の例で言えば、メニューの選択肢は 2 通りで、ドリンクの選択肢は 3 通りなので、あり得るすべての組み合わせの数は 「2 通り × 3 通り = 6 通り」というように求められます。これが関の法則です。

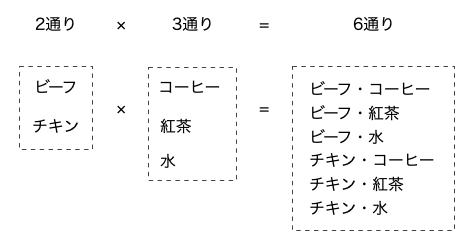
和の法則

組み合わせの数を計算で求めるもう 1 つの方法が、この和の法則です。これは下図のように、樹形図における ワンブロック（点線で囲んだ部分）の組み合わせの数が 3 通りで、ブロックが 2 つだとしたら、すべての組み合わせの数は 3 + 3 = 6 という足し算で求められるというものです。

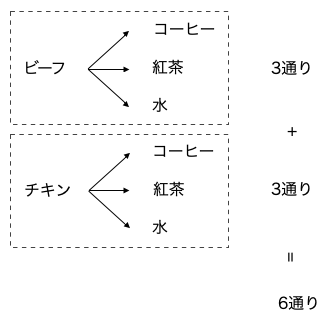
計算としては関の法則と全く同じですが、選択肢の数に注目するのか、ワンブロックの中の組み合わせ数に注目するのかという点で発想の違いがあります。どちらの発想もできるようになっておくと何かと便利です。

3. 練習問題

それでは場合の数の理解をより深めるために、ここでは練習問題を解いてみましょう。問題は 2 つ用意していますので、ぜひチャレンジしてみてください。

試合の勝敗の場合の数

まず樹形図を書いてみましょう。

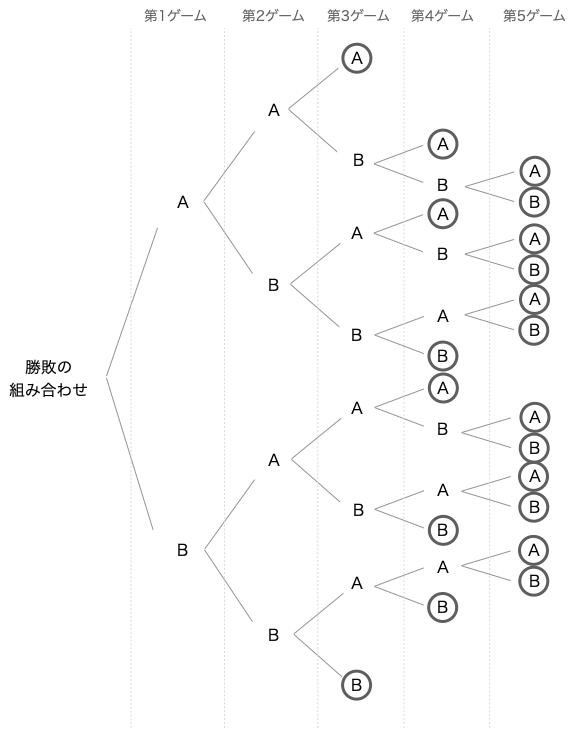
このように全部で 20 通りになることがわかります。

なお、上で解説した積の法則や和の法則を理解していれば、「A が勝つパターンと B が勝つパターンが同数になる」ことが分かり、さらに、このことから答えは必ず偶数になることがわかります。樹形図に加えて、これらのことを意識しておけば間違いを大きく減らすことができます。

以上のように、樹形図・積の法則・和の法則を知っていれば、「場合の和」を求める問題のほとんどは解けるようになりますので、しっかりと抑えておきましょう。

道順の場合の数

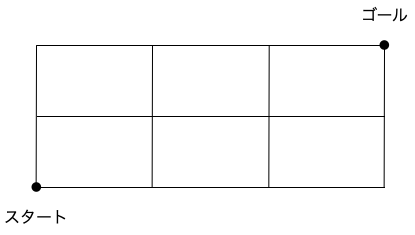
これは最短経路が条件なので、左に進む、下に進むという選択肢はありません。どのような経路を進むとしても、右に 3 回、上に 2 回の移動になります。つまり、これは「右・右・右・上・上」という 2 種類の同じものを含む合計 5 つの要素から 5 つを選んで並べる方法が何通りあるか、という問題と同じものであると解釈できます。

そして、これの答えを求めるには次のように計算します。

以上のことから答えは 10 通りになります。

この P や C などの記号を使った計算は、以下の 2 つのページをご覧いただければ、すぐに理解できるようになるので、ぜひご確認ください。どちらも場合の数の算出をとても簡単にしてくれる必須の内容です。

• 『順列とは？理解しておきたい4つの公式と計算方法』
• 『組み合わせとは？絶対に知っておくべき 2 つの公式と計算のパターン』

まとめ

以上が場合の数です。

ここでは場合の数の求め方として、樹形図と積の法則・和の法則を紹介しましたが、場合の数を求めるために便利かつ必須のツールは他にもいくつかあります。そのうち次に押さえておきたいのが「集合」です。

そこで、当ページのあとは是非『集合とは？覚えておくべき 6 つの記号と 1 つの法則』へと読み進めてください。確率論について理解するために下地をしっかりと築くことにつながります。