マルコフ連鎖モンテカルロ法を誰でも理解できるようにわかりやすく解説

2021 11/09

2021年11月9日 2021年11月9日

マルコフ連鎖モンテカルロ法（MCMC）は、ベイズ推定において、事後分布を求めるのが計算上余りにも困難な場合に、事前分布と尤度分布を材料として乱数を無作為抽出することで、事後分布を概算する方法のことです。

そうは言っても、これだけでは全く意味がわからないと思います。そこで、このページでは、マルコフ連鎖モンテカルロ法について、まずは数式をほとんど使わずにわかりやすく解説していきます。その後に、設定と使用が簡単な統計言語 R を使って、マルコフ連鎖モンテカルロ法を行う方法を簡単に解説します。R 言語は習得が容易ですので、ぜひ試してみてください。

具体的に、この記事では以下の内容を学ぶことができます。

マルコフ連鎖モンテカルロ法を理解するための前提知識であるベイズ推定についてわかりやすくおさらいができる。
マルコフ連鎖モンテカルロ法の、モンテカルロ法と、マルコフ連鎖について理解できる。
マルコフ連鎖モンテカルロ法が、どのように事後分布を概算しているのかがわかる。
R 言語を用いてマルコフ連鎖モンテカルロ法の実践方法がわかる。

それでは早速見ていきましょう。

1. ベイズ推定のおさらい

最初にベイズ推定について、簡潔におさらいしておきましょう。それによって、マルコフ連鎖モンテカルロ法はどういう場合に便利なものなのかがわかりやすくなります。

1.1. ベイズ推定と確率分布

ベイズ推定では確率分布が重要な役割を担っています。確率分布とは簡潔に言うと「パラメータが取り得るすべての値であり、それぞれの値が確率的にどれぐらい見られるのか」を数学的に表したものです。なおパラメータとは、興味のある現象を要約した数値のことです。たとえば成人男性の身長について何かを学びたいとしたら、パラメータはたとえば平均身長といった関心対象の数値のことです。

確率分布の中で最も有名なのは正規分布でしょう。

たとえば身長に関する次のような正規分布があるとします。これは平均値 \(\mu=190\)、標準偏差 \(\sigma = 20\) の正規分布です（身長に関する分布としては平均値・分散ともにが大き過ぎますが、後で使うためにあえてこうしています）。

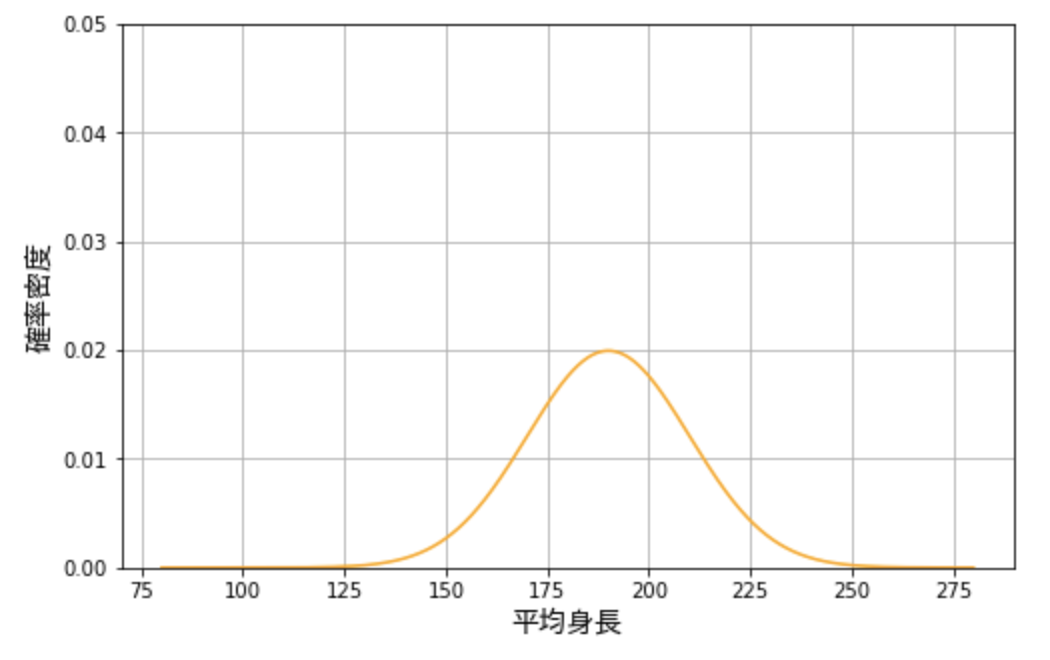
正規分布は、平均値から標準偏差 \(\sigma\) がいくつ分、離れているかによって、そのデータが見られる確率を把握できるという特徴があります。

具体的には、平均の \(190\) から \(± 1 \sigma \) の領域、つまり \(170 \sim 210\) の間に全体の \(68.2\%\) のデータがあります。そして \(± 2-1 \sigma \) の領域、\(150 \sim 170\) と \(210 \sim 230\) の領域には全体の \(27.2\%\) のデータがあります。同じように \(± 3-1 \sigma \) の領域には全体の \(4.2\%\) のデータが、それ以降の部分には全体の \(0.2\%\) のデータがあります。

このように確率分布を活用すると、パラメータについて様々な知見を簡単に得られるようになります。

1.2. 3 種類の確率分布

この確率分布はベイズ推定においては単なる分析ツール以上の意味を持ちます。ベイジアンにとっては、確率分布は、パラメータに対する我々の信念を表したものなのです。そして、これには、

事前分布
尤度分布
事後分布

の 3 種類があります。それぞれ改めて解説します。

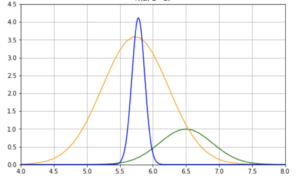
たとえば、ある人が、人間の平均身長は上のグラフに従うと信じているとします。上のグラフは明らかに平均身長が高いので、この信念を持っている人は高身長の人が多い地域で生活しているのでしょう。ベイズ推定では、このように人々がもともと持っている信念を事前確率分布と言います。

さて、この人が世界中の人々の平均身長について興味を持ち、さまざまなデータを調べたところ、以下の青い曲線のように、人々の身長は大体 \(170 ± 20 \) 程度に収まるということを知ったとします。このような実際のデータの分布のことを尤度分布（尤度関数）と言います。これは、興味の対象のパラメータに関して実際に観察したデータを確率分布として要約したものです。

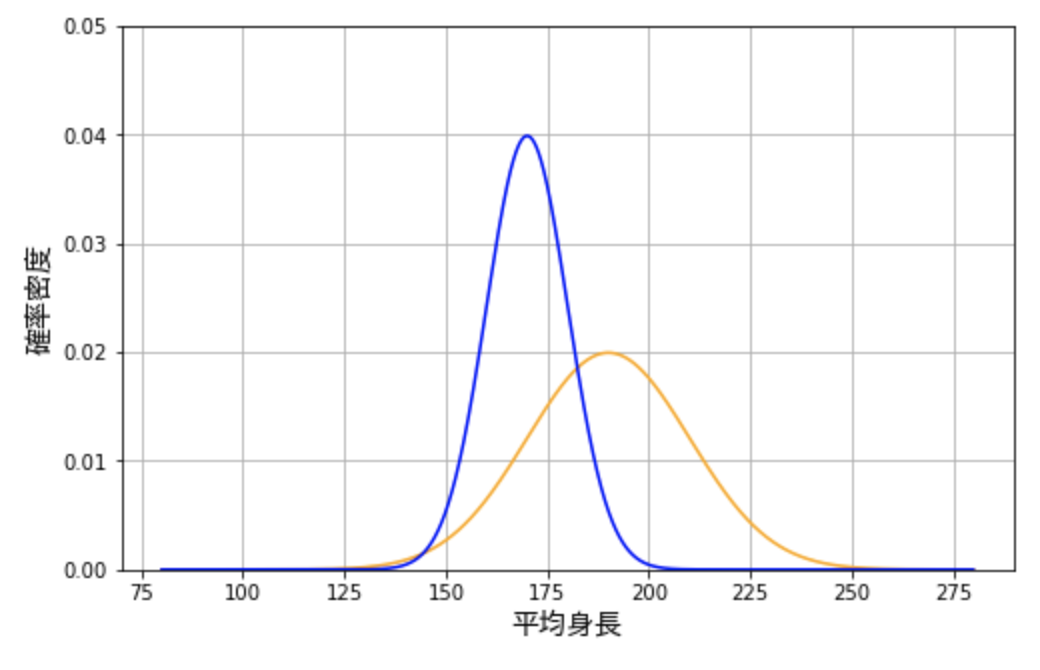
ベイズ推定の肝は、これらの事前分布と尤度分布を組み合わせて、事後分布を求めることにあります。事後分布とは、データを受けてアップデートした新しい信念です。これは、事前分布と尤度分布の平均のようなものと考えても良いでしょう。

今回のケースではこれは以下の赤い曲線のようになります。

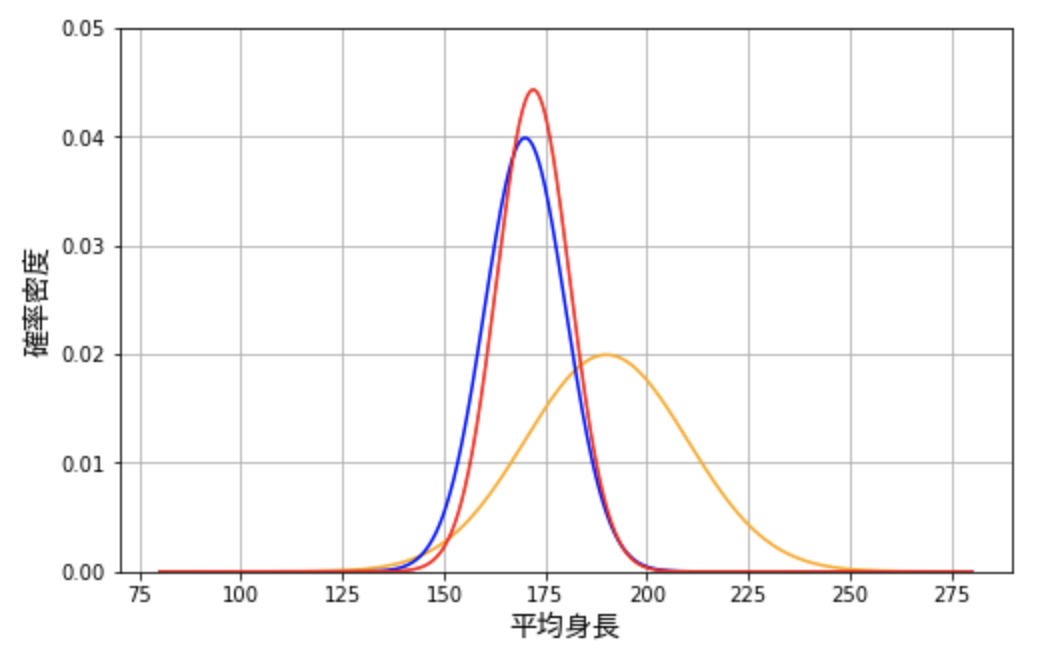
これらの 3 つの確率分布を比較すると次のようなことがわかります。

事前分布は事後分布と比べて、頂点が低く、分散も大きいです。これは平均身長に対する事前の信念はそれほど強くないということを意味しています。一方で尤度分布は頂点が高く、データがより狭い範囲に集まっています。このことから尤度分布は、事前分布よりも確信度合いが高いことがわかります。

これらの事前分布と尤度を組み合わせると、当然データが事前の弱い信念を圧倒します。これはつまり、この事前信念を持っていた、平均身長が高い地域に住んでいる人の考えが大きく変わったことを意味します。ただし、この人は、平均身長はまだ実際のデータよりも高いはずだと考えていることが、事後分布からわかります。

このように事前分布と尤度分布から事後分布を求めるというのがベイズ推定です。

1.3. ベイズ推定においてMCMC が必要な場合

さて、ここまでの例では事前分布も事後分布も両方とも正規分布でした。そのため事後分布を求めるのが非常に簡単でした。このように事後分布を求めるのが簡単な事前分布と正規分布の組み合わせを「共役族」と言います。

代表的な共役族には以下の 3 つがあります。

ベータ分布 – 二項分布
ガンマ分布 – ポアソン分布
正規分布 – 正規分布

これらについて詳しくは、『共役事前分布とは？誰でも必ず理解できるようにわかりやすく解説』で解説しているのでご確認ください。

しかし現実の現象は、こうした共役族の確率分布のようにスッキリしたものばかりではありません。例えば社会的な現実のほとんどは非常に複雑です。下図のように事前分布に頂点が 2 つあったり、尤度分布が複雑な形状をしていたりするのです。

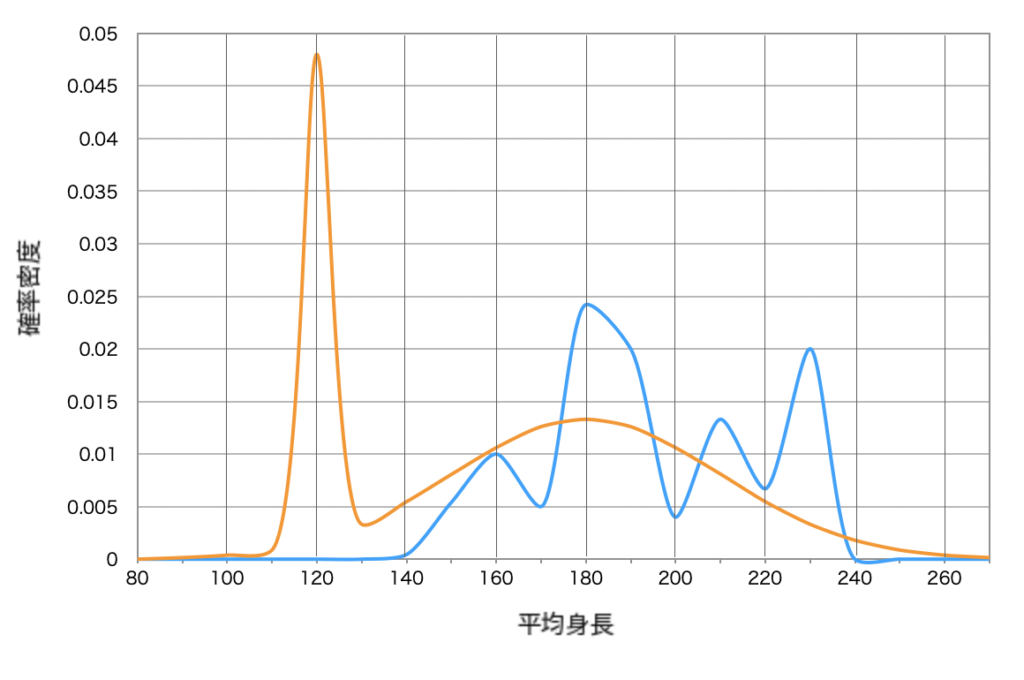
このような場合はどうやったら事後分布を求めることができるのでしょうか。一つ言えることは計算によって、事後分布の確率関数を求めることは、ほとんど不可能だということです。それではどうすれば良いのでしょうか？このような場合こそマルコフ連鎖モンテカルロ法の出番です。

* なお、マルコフ連鎖モンテカルロ法は、事前分布と尤度分布の確率関数が既知である必要があります。なぜなら、この方法は事後分布 \(\propto\) 事前分布 \(\times\) 尤度分布の比率を使うからです。

2. マルコフ連鎖モンテカルロ法とは

マルコフ連鎖モンテカルロ法（MCMC）は、事後分布を直接計算することができない場合に、事後分布の形状を概算することを可能とするメソッドです。なぜ、そのようなことが可能なのでしょうか。これを知るために、まずはモンテカルロ法とマルコフ連鎖に分けてみていきましょう。

2.1. モンテカルロ法とは

モンテカルロ法（モンテカルロ・シミュレーション）とは、乱数を繰り返し生成することによってパラメータを概算する方法です。

たとえば以下の単位正方形に接した円の面積を概算したいとしましょう。

公式から、この円の面積は \(0.5×0.5×3.14=0.785\) であることは簡単に求められます。しかし、ここでは公式を使わずに、モンテカルロ法で求めてみましょう。

この単位正方形の中に完全にランダムに \(20\) の点を落とすとします。そして、その \(20\) の点の内、円の中に落ちたものと、円の外に落ちたものの数の比率を求めます。その比率を正方形の面積に掛ければ、円の面積の良い概算になります。実際にこれを行なって、下図の通り \(15\) 個の点が円の中に、\(5\) 個の点が円の外に落ちたとします。

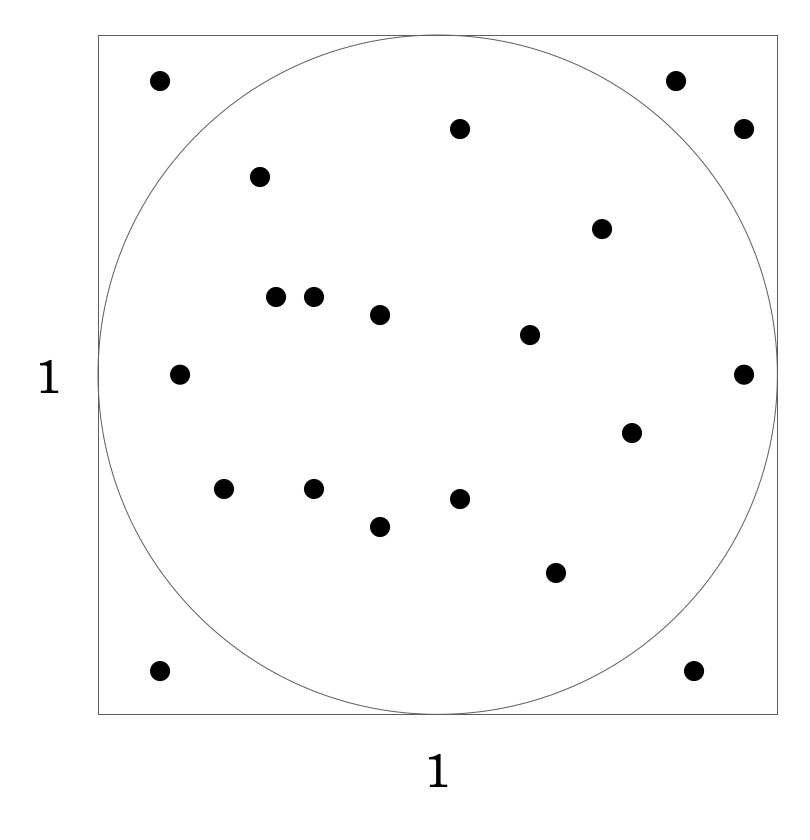
この場合、円の面積は、単位正方形の面積との比率から \(1 × 1 × 15 ÷ 20 = 0.75\) と求めることができます。乱数がたった \(20\) 個にしては良い結果です。この乱数を増やせば増やすほど、概算の値は実際の円の面積に近づいていきます。

このように乱数によって値を概算する手法がモンテカルロ法です。

この方法を使えば、以下のようなバットマン・シンボルの面積でも、公式 \(A=
\dfrac{955}{48}
–
\dfrac{2}{7}
\left[
2\sqrt{33}+7\pi + 3 \sqrt{10}(\pi -1)
\right]
+
\)\(21
\left[
\cos^{-1}
\left(
\dfrac{3}{7}
\right)
+ \cos^{-1} \left(\dfrac{4}{7} \right)
\right]\) を使わずに正確に概算することが可能です。

モンテカルロ法は、このような面積の概算だけではなく、非常に複雑なプロセスのモデリングに使われています。たとえば天気予報や、選挙での勝率などです。

ベイズ推定においても、モンテカルロ法を使うことで、そのままでは計算が複雑すぎて分析できない事後確率分布を、モンテカルロ法の乱数シミュレーションで再現することで、計算することができます。

しかし、ベイズ推定において必要なのは、事後確率分布に沿った乱数ですが、モンテカルロ法をそのまま使うと完全にランダムな乱数が生成されてしまいます。

そのためベイズ統計では、モンテカルロ法で事後分布（\(\propto\) 事前分布 \(\times\) 尤度分布）の乱数が生成されるようにするために、その値が大きい領域（=密度が濃い領域）では乱数が密集し、その値が小さい領域（=密度が薄い領域）では、乱数が点在するように調整を行う必要があります。

要するに、完全にランダムな乱数ではなく、事後分布（\(\propto\) 事前分布 \(\times\) 尤度分布）の複雑な確率関数に沿った乱数が得られるようにしなければならない、ということです。

そのために用いるのがマルコフ連鎖です。

2.2. マルコフ連鎖とは

MCMCの 2 つ目の要素はマルコフ連鎖です。

マルコフ連鎖は単純に、「現在の状態は直前の状態のみに依存するという確率モデル」のことです。この確率モデルの本質は「長期的には、確率は定常状態（定常分布）に収束する」というところにあります。

具体的に見てみましょう。

マルコフ連鎖の最も有名な例は、この概念の生みの親であるアンドリー・マルコフによるものです。彼は、ロシアの詩から何種類もの 2 文字のペアを数え上げました。そして、その 2 文字のペアを使って、それぞれの文字の後にどの文字が来るのかの条件付き確率を求めました。その条件付き確率を使って、マルコフは文章っぽい長い文字列のシーケンスをシミュレートしました。結果、最初のいくつかの文字は、一番最初の文字に大きく依存するが、長期的には、文字の分布は定常分布というパターンに一致するようになるということを発見したのです。

よりイメージしやすい例として、次のような問題を考えてみてください。

あるサービスに関するブランドの A 社と B 社があります。両社はシェアの取り合いに鎬しのぎを削っており、現在、市場はこの 2 社のみが席巻している状態です。そしてお互いに顧客獲得キャンペーンを行っています。そして毎年 4 月 1 日に、すべての顧客は、次の選択肢のうちどちらかを選んでいるとします。

今の会社を使い続ける
一方の会社に乗り換える

顧客は前年のサービス内容だけを考えて、次の年のブランドを選びます。それぞれの確率は次のようになっています。

前年 A 社の人が、今年も A 社を使う確率：0.4
前年 A 社の人が、今年は B 社を使う確率：0.6
前年 B 社の人が、今年も B 社を使う確率：0.1
前年 B 社の人が、今年は A 社を使う確率：0.9

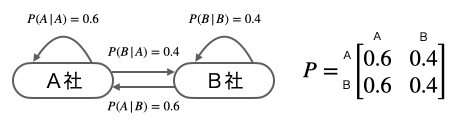
マルコフ連鎖では、こうした一つひとつの確率のことを遷移確率または遷移核と言います。そして遷移確率を、下図のように一目でわかるようにしたものを状態遷移図と言います。そして、隣にある行列は遷移確率の推移を示す遷移確率行列と言います。

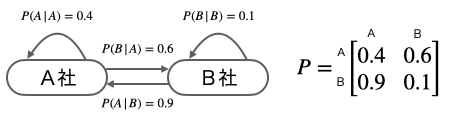
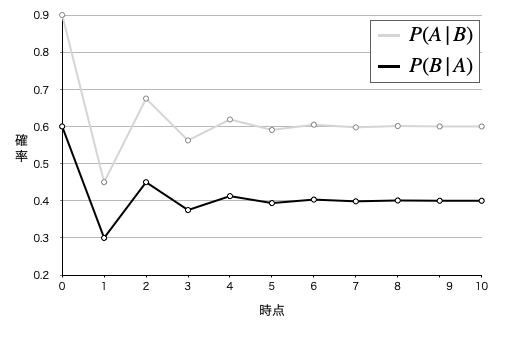
さて、以上のように遷移確率がすべて明らかなとき、この確率モデルが将来的にどうなるかは明確に予測することができます。答えから言うと、最初の状態のユーザー比率がどのようなものであったとしても、最終的に、両者のユーザー比率は A 者が 60% 対 B 社が 40 % に落ち着くのです。

このようにマルコフ連鎖の最終的な状態のことを定常分布と言います。これを示したものが下図です。そして、ある連鎖がこの状態になることを「定常分布に収束する」という風に言います。

ちなみに定常分布は遷移確率行列を、理論上、無限回数、乗算することで求められます（*行列の掛け算については『行列の積(掛け算)とは何か？わかりやすく解説』で解説しています）。

\[\begin{eqnarray}
P^n
=
\begin{bmatrix}
0.4 & 0.6\\
0.9 & 0.1
\end{bmatrix}
\begin{bmatrix}
0.4 & 0.6\\
0.9 & 0.1
\end{bmatrix}
\cdots
\begin{bmatrix}
0.4 & 0.6\\
0.9 & 0.1
\end{bmatrix}
\Rightarrow
\begin{bmatrix}
0.6 & 0.4\\
0.6 & 0.4
\end{bmatrix}
\end{eqnarray}\]

マルコフ連鎖モンテカルロ法は、事後分布の確率関数に沿った乱数を生成するために、マルコフ連鎖のこの「十分に時間が経てば、確率は定常状態（定常分布）に収束する」という性質を利用します。要するに、定常分布が、事後確率分布（\(\propto\) 事前分布 \(\times\) 尤度分布）と同じになるようにすれば良いのです。そうすれば事後確率分布と同じ乱数を得られることになります。

2.3. マルコフ連鎖モンテカルロ法

さて、ここまでで解説したマルコフ連鎖とモンテカルロ法を組み合わせて、事前分布と尤度分布から、事後分布をシミュレートするのがマルコフ連鎖モンテカルロ法です。

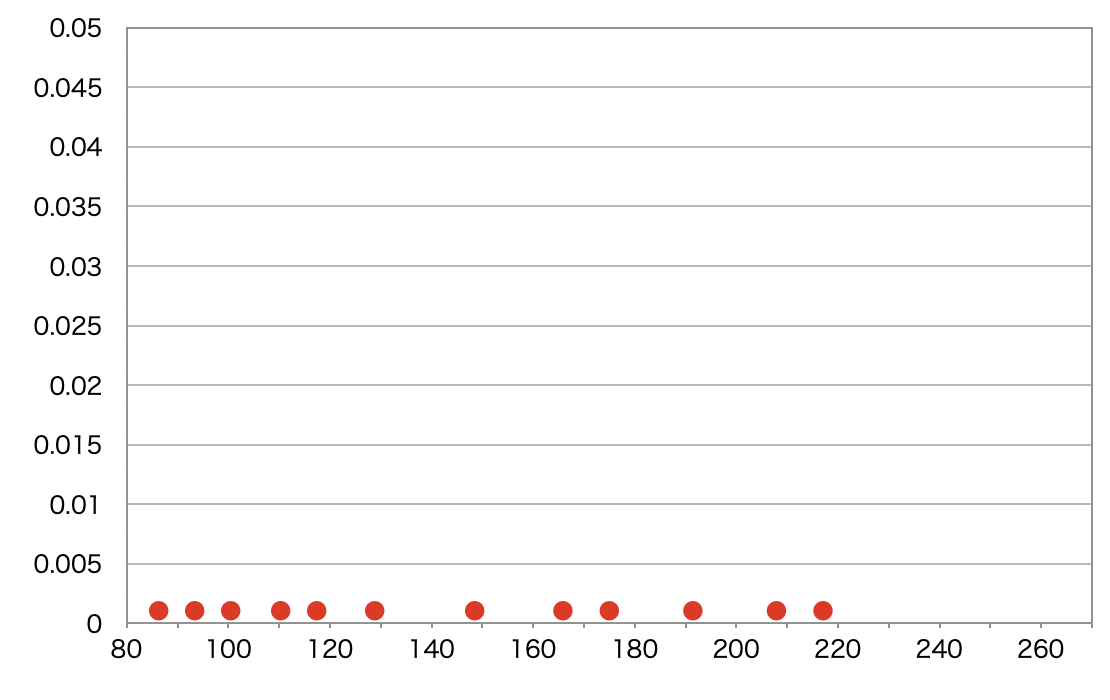
はじめに、MCMC メソッドはパラメータ値をランダムにピックアップします。そしてシミュレーションは、引き続き、乱数を生成し続けます。ここがモンテカルロ法のパートです。下図の赤点がモンテカルロ法によってつけられた乱数だと思ってください。

この乱数は完全にランダムについているわけではありません。最終的に事後分布（\(\propto\) 事前分布 \(\times\) 尤度分布）と同じ定常分布に収束するように条件付けされたマルコフ連鎖の条件式（「詳細釣り合い条件」と言います）の通りに乱数を判定しています。具体的には、今生成された乱数は、直前に生成されたものよりも、条件に合うのか合わないのかが判定され、その度合いに応じて、採用されるか（その点に移動するか）、採用されないか（同じ点に留まるか）が決まるというようになっています。

このマルコフ連鎖のパートによって、最初の数千の乱数を生成して、乱数が定常分布に収束した後は、そこから生成される乱数生成は定常分布とほとんど同じものになっています。これを以下の青点で示しています。

* MCMCでは、定常分布に収束するまでの数千の乱数は「バーン・イン期間」と言って、捨ててしまうことを前提としています。

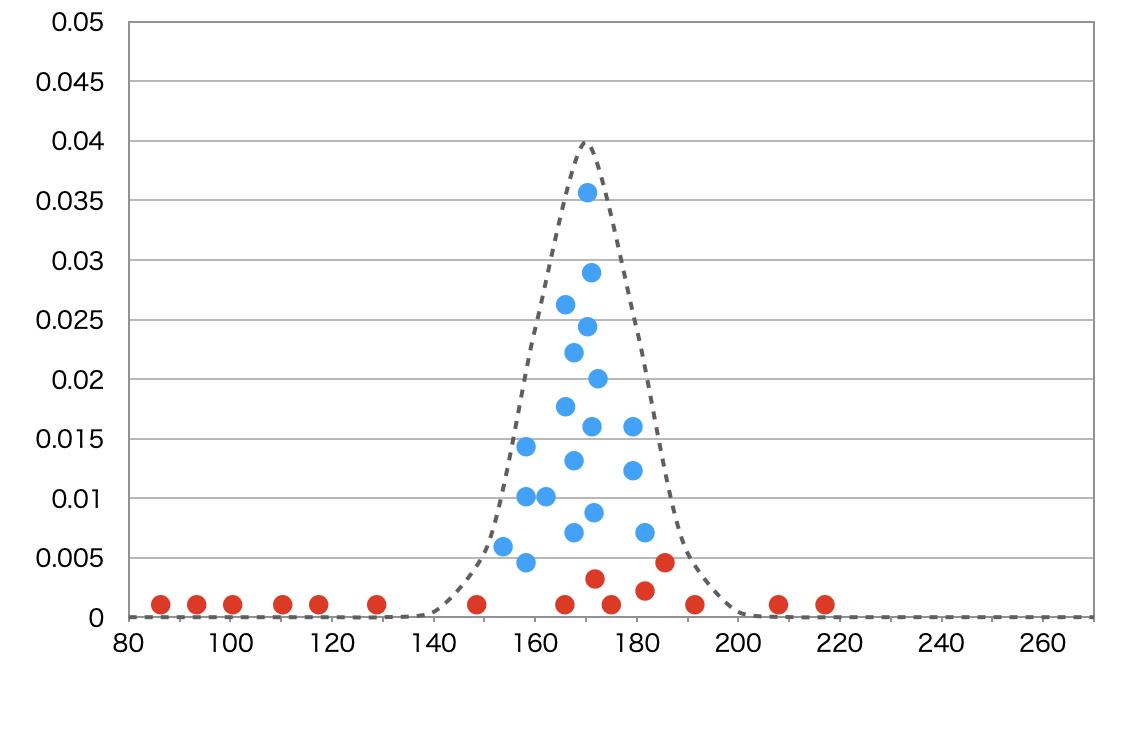
乱数生成が定常分布に収束した後は、MCMCサンプリングは、事後分布からのサンプルを生成します。それらのサンプル点にヒストグラムを描けば、事後分布と同じものを得ることができて、さまざまな統計分析が可能になります。

以上がマルコフ連鎖モンテカルロ法が行なっていることです。

3. R言語でマルコフ連鎖モンテカルロ法

それでは統計プログラミング言語 R の拡張パッケージ rstan を使って、実際に MCMC を行ってみましょう（python の pystan でもほとんど同じように行えます）。

ここでは以下のベータ – 二項共役族を例として、実際に MCMC を行うことにします。

\[\begin{eqnarray}
\pi &\sim& {\rm Beta}(2, 2)\\
Y | \pi &\sim& {\rm Bin}(10, \pi)
\end{eqnarray}\]

\(Y\) は二項分布の確率変数なので、\(10\) 回の試行の中での成功回数です。1 回 1 回の試行の成功率は \(\pi\) であり、事前分布は \({\rm Beta}(2, 2)\) で表されます。

それでは、ここで \(Y=9\) 回の成功というデータを見たとしましょう。この場合、共役族の公式より事後分布は次の通りになります。

\[\begin{eqnarray}
\pi | (Y=9)
\sim
{\rm Beta}(11, 3)
\end{eqnarray}\]

それでは、これを MCMC で求めてみましょう。

3.1. rstan で MCMC を実践

R 言語で MCMC を行うには: (1) ベイズモデルの構造を rstan 記法で定義する、(2) 事後分布をシミュレーションするという 2 つのステップが必要です。

step 1 では、このモデルの構造を定義するために、まず以下の 3 つを特定する必要があります。

data
データ \(Y\) は、10 回の試行回数のうちの成功数です。これは確率変数です。

parameters
パラメータ \(\pi\) は成功率です。

model
データ \(Y\) は \(\rm{Bin}(10, \pi)\) モデルで定義され、事前分布は \(\rm{Beta}(2,2)\) で定義されます。

これらのベータ−二項共役構造を R言語の rstan 構文に書き換えたものが以下のコードです。

# パッケージのインストール
library(“tidyverse”)
library(“janitor”)
library(“stan”)
library(“bayesplot”)

# モデル定義
test_model <- “
data {
　int<lower=0, upper=10> Y;
}
parameters {
　real<lower=0, upper=1> pi;
}
model {
　Y ~ binomial(10, pi);
　pi ~ beta(2, 2);
}
“

step 2 では、stan() 関数を使って、事後分布をシミュレートします。大雑把に言うと、stan() 関数は、ベータ−二項モデルの事後分布の擬似乱数を生成するために MCMC のアルゴリズムを起動するものです。

これは R 言語に次のように打ち込みます。

test_sim <- stan(model_code = test_model, data = list(Y = 9),
chains = 4, iter = 5000*2, seed = 84735)

stan() 関数には 2 種類の引数が必要です。1 つ目はモデルの情報を指定するものです。

model_code : 定義したモデル名（ここでは test_model）
data : 観察データのリスト（ここでは Y=9）

2 つ目は、マルコフ連鎖の情報を指定するものです。

chains : いくつの連鎖にするかを指定します。ここでは 4 つの連鎖にします。そのため、\(\pi\) の値も 4 つ得られます。
iter : それぞれのマルコフ連鎖の長さ（イテレーションの数）を指定します。デフォルトでは、最初の半分のイテレーションはバーン・イン（ウォーム・アップ）サンプルに使われ、残りの半分は最終的なマルコフ連鎖のサンプルに使われます。
seed : 乱数を固定するためのものです。

test_sim に保管される結果は、stanfit オブジェクトです。このオブジェクトには、4 つのマルコフ連鎖を 10,000回イテレーションしたものが含まれています。それぞれ最初の 5000 はバーン・インに使われているので、最終的には 5000 ずつのマルコフ連鎖のサンプルが得られます。

最初の 4 つの値は以下に載せておきます。

as.array(test_sim, pars = “pi“)
head(4)

これらのマルコフ連鎖の値は、事後分布から取った無作為標本でもなければ、独立しているわけでもありません。そういうよりもむしろ、それぞれの 4 つの鎖は、互いに依存した長さ 5000 の \(\pi\) の値のマルコフ連鎖 \((\pi^{(1)}, \pi^{(2)},…\pi^{(5000)},)\) を形成します。

例えば、イテレーション 1 では、chain:1 はだいたい \(\pi=0.9402\) で始まり、イテレーション 2 では \(0.9301\) になっています。同じように chain2 は \(0.8777, 0.9801,…\) と動いています。

つまり、連鎖は、標本空間または事後分布の尤もらしい \(\pi\) の値の範囲を上下動しています。マルコフ連鎖のトレース・プロット（下図）は、この上下動を示しています。縦軸が \(\pi\) の値で、横軸がそれぞれのイテレーションです。

mcmc_trace(bb_sim, pars = “pi“, size = 0.1)

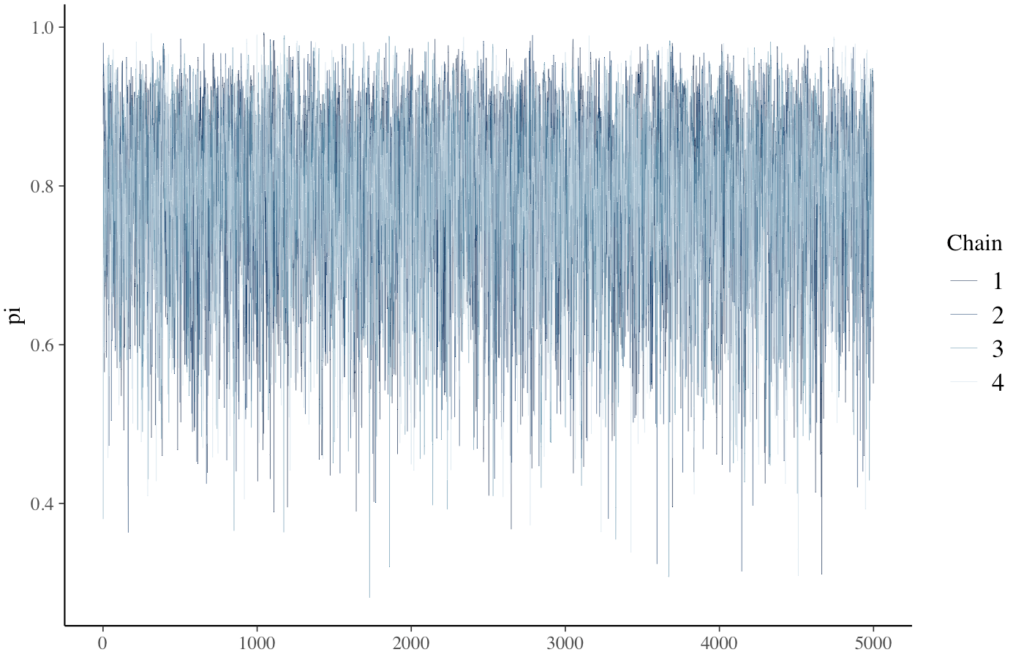
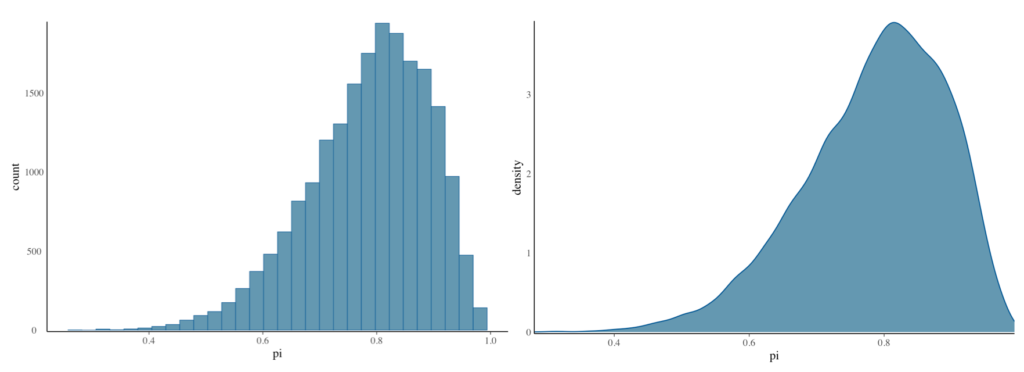
下図のヒストグラムと確率密度プロットが、今回マルコフ連鎖の乱数が訪れた値のスナップショットです。

mcmc_hist(bb_sim, pars = “pi“) +
　yaxis_text(TRUE) +
　ylab(“count“)

mcmc_dens(bb_sim, pars = “pi“) +
　yaxis_text(TRUE) +
　ylab(“density“)

マルコフ連鎖の値の分布は、\({\rm Beta}(11,3)\) の非常に良い近似となっていることがわかります。

以上が R による MCMC の実践です。

3.2. MCMCの診断方法

以上のMCMCの例で、マルコフ連鎖がパラメータ \(\pi\) の標本空間を横断して、最終的に事後分布に収束する無作為標本を模倣することを見てきました。ここで以下のような疑問が出てきます。

良いマルコフ連鎖はどのように見えるのか？
マルコフ連鎖の標本が事後分布の合理的な近似であると、どのように言えるのか？
マルコフ連鎖のサイズはどれぐらい大きくあるべきか？

これは一概に白黒で答えられるものではありません。良いマルコフ連鎖がどのように見えるのかや、良くないマルコフ連鎖をどのように直すのかが分かるようになるには経験を要します。しかし、それでは何も前に進まないので、判断材料として、この章ではトレース・プロットのチェック方法について解説します。

* なお、MCMC の診断には経験が必要です。またトレース・プロットのチェック以外にも、パラレル・チェーンの比較や Rハットを使った確認方法もあります。これらすべてを解説すると、分量が大きくなり過ぎるので、ここでは割愛します。更なる学習については、R を使ったベイズ統計の専門書籍をお求めください。

さて、上で見たトレース・プロットは、まさに理想的で教科書的なものです。対照的に、下図のようなトレース・プロットの場合は立ち止まる必要があります。

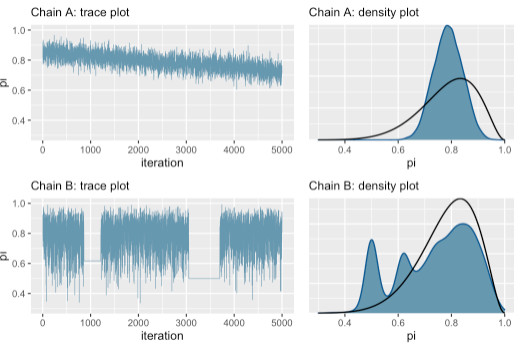
まずは上の図の左側をご覧ください。明らかに右肩下がりのトレンドが見られます。これは 5000 のイテレーションでは、マルコフ連鎖がまだ定常分布の状態で安定していないことを示しています。もしくは、右肩下がりのトレンドは、連鎖の一つ一つの値の相関関係を示唆するもので、一つ一つが独立していないことを示唆しています。

下側の図もまた異なる問題を見せています。トレース・プロットに見られる 2 つの水平ラインがそれを示しています。さらに、右側の密度プロットを見ると、誤った事後分布になっていることがわかります。

これらのようなトレース・プロットになったときは、以下の 2 つの方法を試してみましょう。