tan の積分は -log|cos(x)| になります。ここでは、なぜこうなるのかについて、イメージによって直感的に理解する方法と、数式によって理解する方法の２通りを解説します。
微積分に対する本質的な理解を得るための助けとなりますので、ぜひご覧頂ければと思います。
1. tan(x) の積分公式
\(\tan(x)\) の積分公式は次の通りです。
\(\tan(x)\) の不定積分
\[\begin{eqnarray}
f(x)=\tan(x)
\hspace{5mm}
\overset{\textrm{積分}}{\underset{\textrm{微分}}{\rightleftarrows}}
\hspace{5mm}
F(x)=-\log|\cos (x)|\
\end{eqnarray}\]
なぜ、こうなるのかをイメージによる直感的な理解に頼る方法と、数式に頼る方法の２通りで解説することにします。受験勉強では数式に頼る方法のみを習うと思いますが、それでは実世界の問題解決のための実践力はつきません。公式を使って数学問題をパズルのように解くことができるということと、数学を理解しているということは全くの別物なのです。
そこで数学の理解を深めるためにも、イメージによる直感的な理解もできるようになっておきましょう。
1.1. イメージで確認
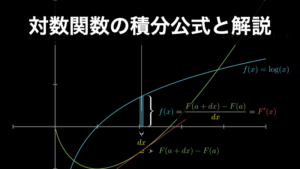
\(\tan(x)\) の積分公式は以下の画像で視覚的に確認できます。
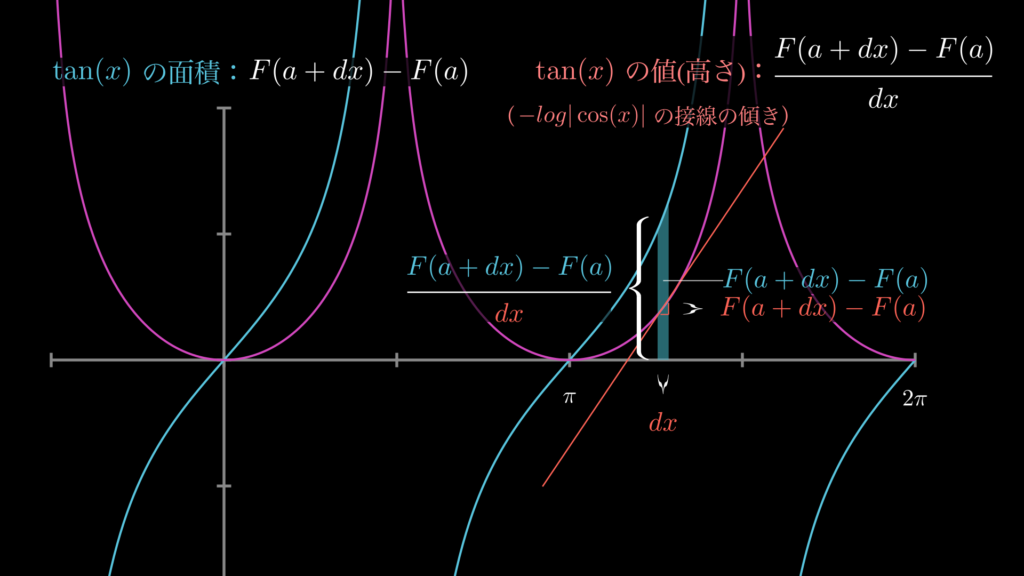
簡潔に解説します。
まず、『積分とは何か？最もわかりやすく簡単に理解できるように解説』で解説している通り、\(f(x)=\tan(x)\) の任意の区間の積分とは、その区間における面積 \(F(a+dx)-F(a)\)のことです。
そして、この面積における長方形の底辺の長さが \(dx\) であるため、この長方形の高さは \(\frac{F(a+dx)-F(a)}{dx}=F^{\prime}(x)\) で求められます。そして、当然、この長方形の高さは \(f(x)\) と等しくなります。以上のことから \(F^{\prime}(x)=f(x)\) となり、公式が正しいことがわかります。
なお上図では \(dx\) を大きく見せているため、その面積は長方形には見えませんが、実際には \(dx\) は限りなくゼロに近い値なので、その面積は長方形と考えて問題ないことになります。この点についてよくわからない場合は『微分とは何か？誰でもわかりやすく理解できるようにイメージで解説』をご確認ください。
なお、積分は微分の逆演算であることは『sin の積分はなぜ -cos ？積分と微分の関係を誰でもわかるように解説』や『cos の積分はなぜ sin？積分と微分がよりよく分かるようになる解説』もご覧頂くと、よりよく分かるようになりますので、ぜひご覧ください。
1.2. 数式で確認
\(\tan(x)\) の積分公式は以下の通り、数式によっても確認することが可能です。
\[\begin{eqnarray}
\int\tan(x)dx
&=&
\int\frac{\sin(x)}{\cos(x)}dx\\
&=&
\int -\frac{\cos^{\prime}(x)}{\cos(x)}dx \\
&=&
-\log|\cos(x)|
\end{eqnarray}\]
解説します。
まず三角関数の定義上、\(\tan(x)=\frac{\sin(x)}{\cos(x)}\) です。そのため、\(\int\tan(x)dx=\int\frac{\sin(x)}{\cos(x)}dx\) と書き換えることができます。
次に『sin の積分はなぜ -cos ？積分と微分の関係を誰でもわかるように解説』で解説している通り、\(\sin(x)\) の積分は \(-\cos(x)\) です。このことから \(\int\frac{\sin(x)}{\cos(x)}dx=\int -\frac{\cos^{\prime}(x)}{\cos(x)}dx\) と書き換えることができます。
最後に、公式より \(\int\frac{f^{\prime}(x)}{fx}dx=\log|f(x)|\) となることが証明されています。そのため、\(\int -\frac{\cos^{\prime}(x)}{\cos(x)}dx=-\log|\cos(x)|\)となります。
以上が公式による証明です。
2. tan^2(x) の積分
それでは補足として、\(\tan^2(x)\) の積分も考えてみましょう。これは試験問題ではよく目にしますが、現実世界ではまず使うことのない関数なので、公式を用いて単に数学パズルとして解くだけで十分です。
言い換えると、数学パズルは、受験で高得点を取るためなら知っておいた方が良いでしょうが、現実世界の問題解決にはあまり役に立ちません。目的に応じて、読み進めるかどうか決めて頂ければと思います。
以下のようになります。
\[\begin{eqnarray}
\int\tan^2(x)dx
&=&
\int\frac{\sin^2(x)}{\cos^2(x)}dx\\
&=&
\int \frac{1-\cos^{2}(x)}{\cos^2(x)}dx \\
&=&
\int \left( \frac{1}{\cos^2(x)}-1 \right)dx\\
&=&
\tan(x)-x
\end{eqnarray}\]
ご覧のように、以下の三角関数の公式を使えば比較的簡単に導き出すことができます。
\[
1+tan^2(x)=\frac{1}{\cos^2(x)}\\
\tan^{\prime}(x)=\frac{1}{\cos^2(x)}
\]
なお二つ目の、\(\tan\) の微分公式については、『tanの微分の公式と証明が誰でも必ずわかるようになる解説』で詳しく解説していますので、ぜひご覧ください。
3. tan^n(x) の積分
それでは、\(\tan^n(x)\) の積分はどうなるでしょうか。これは次のように公式化できます。
\[\begin{eqnarray}
\int\tan^n(x)dx
&=&
\int \left( \frac{1}{\cos^2(x)}-1 \right)\tan^{n-2}xdx\\
&=&
\int \frac{\tan^{n-2}x}{\cos^2(x)}dx-\int \tan^{n-2}xdx\\
&=&
\frac{1}{n-1}\tan^{n-1}x-\int \tan^{n-2}xdx
\end{eqnarray}\]
これの最後の部分の変換 \(\int \frac{\tan^{n-2}x}{\cos^2(x)}dx \rightarrow \frac{1}{n-1}\tan^{n-1}x\) も \(\tan\) の微分公式 \(\tan^{\prime}(x)=\frac{1}{\cos^2(x)}\) を用いたものです。
4. tanの積分のまとめ
以上が tan の積分です。
現実世界の問題解決が目的の場合でも、試験勉強が目的の場合でも、三角関数の積分においては、sin と cos の方が重要ですので、あくまでも、それらを先にマスターするようにしましょう。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント
コメント一覧 （2件）
「不定」積分なのに積分定数がありませんね。
大変わかりやすい記事ありがとうございます、3Blue1Brownの動画を一部切り取りするなのらばクレジットとして示すべきではないでしょうか