対数関数は、微積分に重要な４つの関数（ベキ乗関数・三角関数・指数関数・対数関数）のうちの一つであり、例えば次のような自然現象に現れる関数です。
- 水素イオンの指数を示すpH
- 騒音の程度を示すフォーン
- 地震の強さを示すマグニチュード
- 星の明るさを示す光度
ここでは、この対数関数の積分について、直感的な方法と数式を用いた方法の両方で理解できるように解説していきます。
1. 対数関数の積分公式
早速ですが、対数関数の積分公式は以下の通りです。
対数関数の積分公式
\[\begin{eqnarray}
\int \log x \ dx
&=&
x \log x – x\\
\end{eqnarray}\]
試験対策が目的であれば、これをこのまま暗記しておけば良いでしょう。ここでは、もう一歩進んで、なぜこうなるのかを考えてみましょう。
2. 対数関数の積分公式の証明
ここでは２通りの方法で解説を行います。幾何学的な方法と数式による方法です。教科書では数式による方法ばかりが載せられていますが、それでは数学パズルに習熟するだけであって、本質的な理解を得られることにはなりません。
積分というものを直感的に理解するには幾何学的（視覚的）に理解するのが、とても役に立つのです。そのような理由で、まずは幾何学的な方法の解説から行いたいと思います。
なお、積分を直感的に理解できるようになるための前提として、以下の２記事は先に確認して頂ければと思います。
それでは見ていきましょう。
2.1. 微積分の基本定理で幾何学的に解説
まずは幾何学的（視覚的）に確認しましょう。
対数関数の積分公式は「微分積分学の基本定理（＝積分は微分の逆演算）」から地道に導き出されているものです（というよりも実はすべての積分公式は、地道に微分の逆演算を繰り返して導き出されたものです。）。
そして以下のように、\(x \log x- x\) を微分すると \(\log x\) になることが確認できます。
これを視覚的に表すと以下の通りになります。
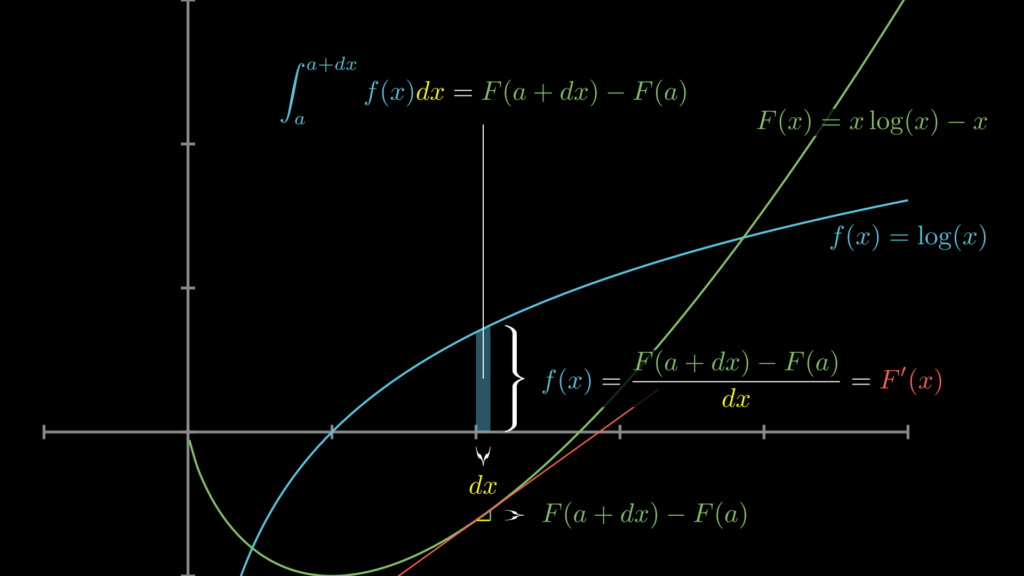
簡単に解説します。
まず微分積分学の基本定理より、[\(a, d+dx\)] 区間の \(f(x)\) の面積は \(F(a+dx)-F(a)\) です。ということは反対に考えれば、この面積を \(dx\) で割ったものが、その区間における \(f(x)\) の値であるということになります。そして、その計算式 \(\frac{F(a+dx)-F(a)}{dx}\) は、そのまま微分の定義式です。以上から、\(F^{\prime}=fx\) となります。
2.2. 部分積分法を用いて数式で解説
次に数式で見てみましょう。
対数関数の積分公式を数式で理解するには、「部分積分法」という公式を応用した証明を用いるのが一般的です。
部分積分法とは以下の公式です。
部分積分法の公式
\[\begin{eqnarray}
\int f \cdot g^{\prime}dx=f \cdot g- \int f^{\prime}\cdot g \ dx
\end{eqnarray}\]
この公式を用いるために、関数 \(\log x\) を \(\log x \cdot 1\) という合成関数であると仮定します。すると以下のように、公式を導き出すことが可能になります。
\[\begin{eqnarray}
\int \log x dx
&=&
\int \log x \cdot 1dx \\
&=&
\log x\cdot x – \int \frac{1}{x} \cdot x \ dx \\
&=&
x \log x -x
\end{eqnarray}\]
※ \(f^{\prime}=\log^{\prime}x=\frac{1}{x}\), \(g^{\prime}=x^{\prime}=1\), \(g=x\)
以上が数式による解説です。
3. 対数関数の積分まとめ
以上が対数関数の積分です。
もし解説にピンと来ない場合は、冒頭でも触れた以下の２つのページをしっかり復習するようにしてください。
これらのページで解説しているように、数学は、数式パズルだけで理解している場合よりも、幾何学的（直感的）な方法でも理解している場合の方が、遥かに本質に近づくことができます。
ぜひ参考になればと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント