cos の積分は sin になります。なぜなら、積分は微分の反対であり、sin を微分すると cos になるからです。とは言っても、これだけで終わってしまっては、あまりにも事務的であり、数学に触れていることにはなりません。
そこで、このページでは、なぜこうなるのかを、誰でも直感的に理解できるように詳しく解説していきます。読み進めていただくと、積分や微分というものが、より深くわかるようになるので、ぜひご覧ください。
1. cos の積分は sin
定義上、積分と微分は正反対の演算です。つまり微分をしたら \(\cos(x)\) になる関数である \(\sin(x)\) が積分です。
\(\cos(x)\) の不定積分は \(\sin(x)\)
\[\begin{eqnarray}
f(x)=\cos(x)
\hspace{5mm}
\overset{\textrm{積分}}{\underset{\textrm{微分}}{\rightleftarrows}}
\hspace{5mm}
F(x)=\sin(x)
\end{eqnarray}\]
それでは、なぜこうなるのでしょうか？
その理由は「積分は微分の反対だから」なのですが、ただ、これを鵜呑みにしているだけでは、積分の本質を理解していることにはなりません。そこで、この点について、より深く、かつ直感的に理解できるように解説しておきたいと思います。
2. なぜ cos の積分は sin になるのか
まず「積分とは何か」で、「関数 \(f(x)\) にとっての積分 \(F(x)\)とは、面積を求めるための掛け算であり、関数 \(F(x)\) にとっての微分 \(f(x)\) とは、高さを求めるための割り算である」ということをお伝えしました。
そして「sin の積分はなぜ -cos ？積分と微分の関係を誰でもわかりるように解説」では、同じことを、任意の区間における \(f(x)\) の平均値と \(F(x)\) の傾きの関係を使って別視点から解説しました。
積分を深く直感的に理解したいという場合は、以上の２つのページは必ず読み込んでおいてください。ここからは、これらについて理解している前提で、\(\cos(x)\) の積分を視覚的に確認していきましょう。
2.1. cos の平均値は sin の傾きと等しい
まずは以下の画像をご確認ください。これは [\(\frac{\pi}{2}, \frac{3\pi}{2}\)] の間の \(\cos(x)\) の面積と平均値を示しているものです。
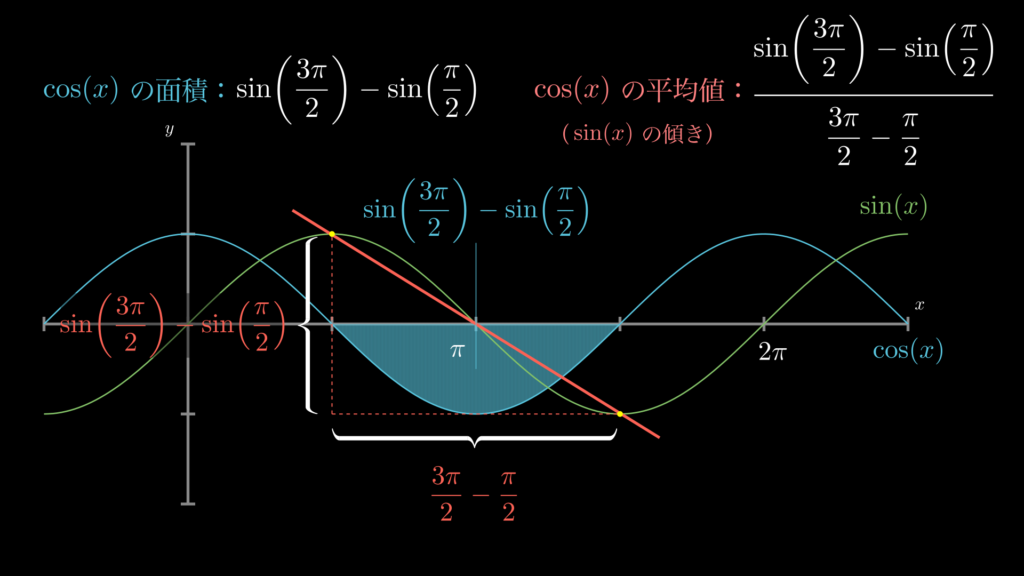
解説します。
ご覧の通り、\(\cos(x)\) の不定積分は \(\sin(x)\) なので、「微分積分学の基本定理」より、面積 \(\int^{\frac{3\pi}{2}}_{\frac{\pi}{2}}\cos(x)dx\) は次のように求められます。
\(\cos(x)\) の定積分（＝面積）
\[\begin{eqnarray}
\int^{\frac{3\pi}{2}}_{\frac{\pi}{2}}\cos(x)dx
&=&
\sin(\frac{3\pi}{2})-\sin(\frac{\pi}{2})\\
\end{eqnarray}\]
そして同区間の平均値（高さの平均）は、この面積から区間の範囲を割ることで求められます。
\(\cos(x)\) の平均値（=高さの平均）
\[\begin{eqnarray}
\frac{\int^{\frac{3\pi}{2}}_{\frac{\pi}{2}}\cos(x)dx}{\frac{3\pi}{2}-\frac{\pi}{2}}
=
\frac{\sin(\frac{3\pi}{2})-\sin(\frac{\pi}{2})}{\frac{3\pi}{2}-\frac{\pi}{2}}
\end{eqnarray}\]
ポイントは、[\(\frac{\pi}{2}, \frac{3\pi}{2}\)] 間の \(\cos(x)\) の平均値（高さの平均）は、その不定積分 \(\sin(x)\) の傾きと同じ値になるという点です。
2.2. cos の値は sin の微分の値と等しい
さて、「微分とは何か」で解説した通り、微分とは接線の傾きです。ということは、ここまでは [\(\frac{\pi}{2}, \frac{3\pi}{2}\)] 間を見てきましたが、この区間を [\(a, a+dx\)] というように狭くすると、\(\cos(x)\) の平均値（=高さ）が、その不定積分である \(\sin(x)\) の微分と同じ値になることがわかります。
以下の画像でご確認ください。
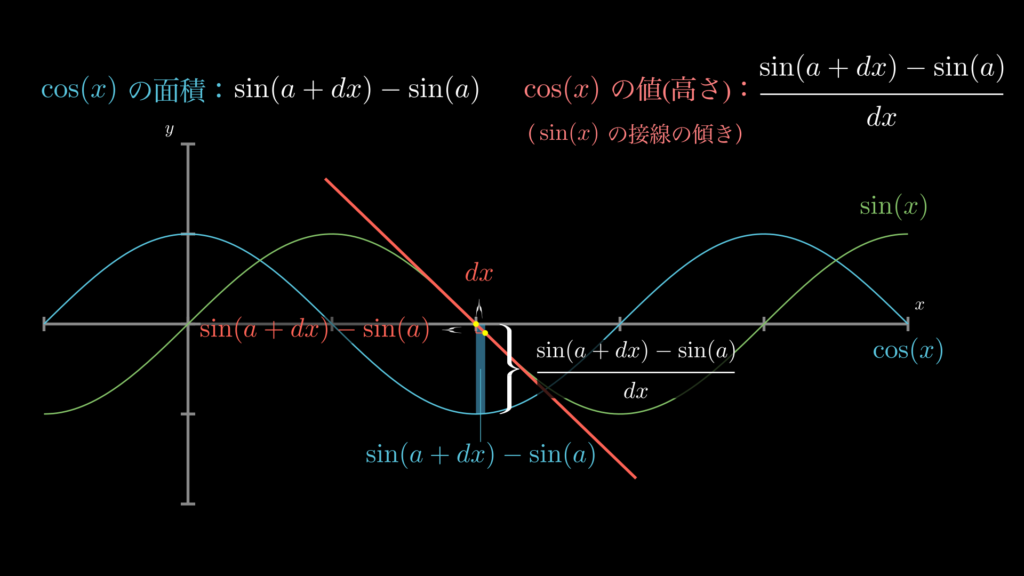
この通り、積分や微分を求めるときのように、\(dx\) の値を \(0\) に近づけていくと（範囲を狭めていくと）、\(\cos(x)\) と \(\sin(x)\) がお互いに積分と微分の関係であることがわかりますね。
3. cosの積分のまとめ
以上が、\(\cos(x)\) の積分が \(\sin(x)\) であり、\(\sin(x)\) の微分が \(\cos(x)\) であることの視覚的な証明です。
ぜひ、しっかりと理解できるように何度も読み返してみてください。また、その際は、『積分とは何か？最もわかりやすく簡単に理解できるように解説』と『sin の積分はなぜ -cos ？積分と微分の関係を誰でもわかりるように解説』も読み返すようにすると理解がより深まるでしょう。
参考にして頂ければ嬉しく思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント