1/x の積分公式と知っておきたい面白い性質

2021 7/09

2021年7月9日

関数 1/x は、微積分に重要な４つの関数（ベキ乗関数・三角関数・指数関数・対数関数）のうちのベキ乗関数に当たるものであり、現実世界の現象の中に特によく現れる関数（y=ax・y=x^2・ y=1/x・ y=sin x）の１つでもあります。

面白いものを挙げると、私たち人間の所持金の消費傾向といった人間関係・紛争関係は、この関数で表されます。また、万有引力・原子斥力・クーロン力といった物理現象もこの関数で表されます。要するに 1/x はシンプルでありながら、非常に重要な関数なのです。

ここでは、この重要な関数の積分について詳しく見ていきたいと思います。

1. 1/x の積分

ここでは、まず \(\frac{1}{x}\) の積分の答えを示し、次にそうなる理由について解説します。

1.1. 公式

関数 \(y=\frac{1}{x}\) の積分は以下の通りです。

ベキ乗関数の不定積分

\[\begin{eqnarray}
\int \frac{1}{x}dx
=
\log x
\end{eqnarray}\]

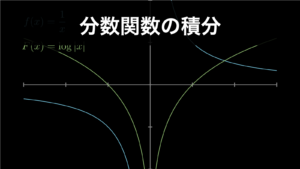
これを視覚的に示したものが以下の画像です。この画像の解釈の仕方については『sin の積分はなぜ -cos ？積分と微分の関係を誰でもわかるように解説』で解説しています。

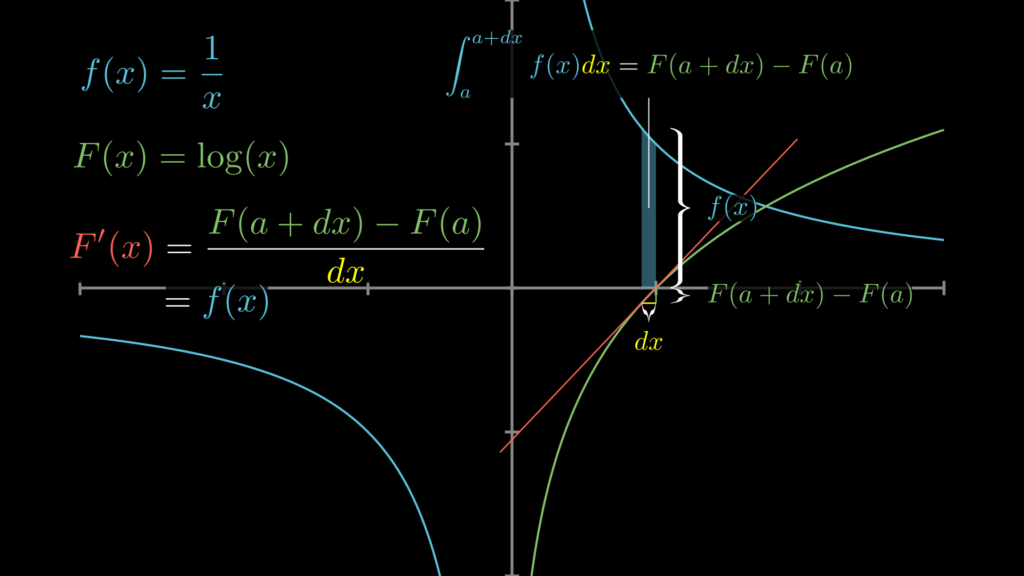
なお、全区間で定義したい場合は、\(\log|x|\) と書きます。

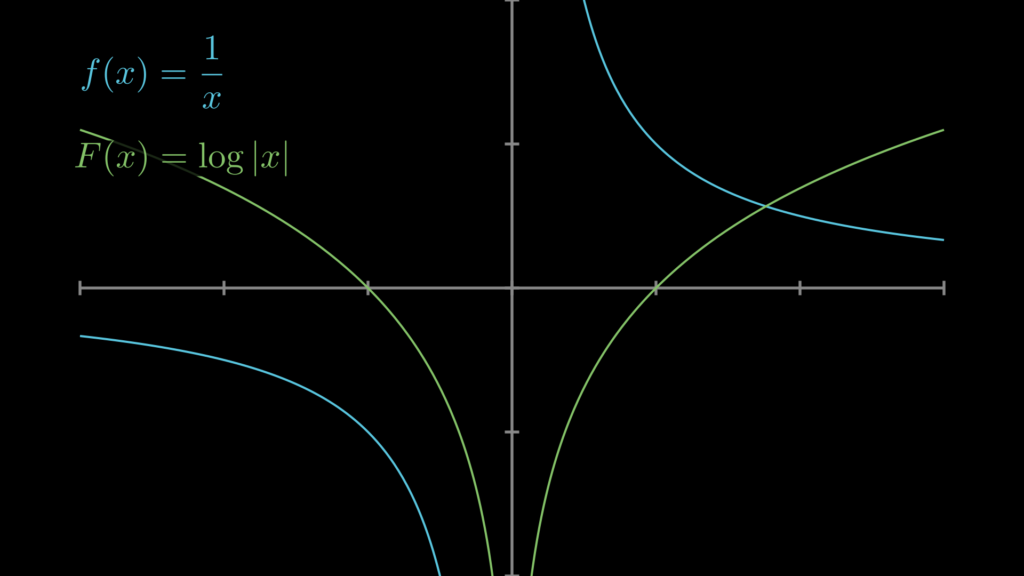
この積分は、試験で頻出するので余り深く考えずに、そのまま暗記しておくように教わることでしょう。その場合、テストで高得点を取ることが目的なので、それでも良いのですが、実は \(\frac{1}{x}\) の積分はとても面白い関数であり、丸暗記で終わらせるのはとても勿体ない関数でもあります。

そこで、一歩進んで、なぜこうなるのかを考えてみましょう。

1.2. 解説

なぜ \(\frac{1}{x}\) の積分は \(\log x\) になるのでしょうか。

本来、\(\frac{1}{x}=x^{-1}\) なので、以下に示しているベキ乗関数の微積分の規則性に従って、\(\int x^{-1}dx=x^0\) になりそうなものです。

ベキ乗関数の微積分の規則性

\[
\begin{array}{ccc}
F(x): & -\dfrac{1}{2}x^{-2} & -x^{-1}& \overbrace{\log x}^{\ast x^0ではない} & x \ \ & \ \ \dfrac{1}{2}x^2 \ \ & \ \ \dfrac{1}{3}x^3 \ \ \\
& \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow\\
f(x): & x^{-3} & x^{-2} & x^{-1} & x^0 & x^1 & x^2\\
& \downarrow & \downarrow & \downarrow & \downarrow & \downarrow & \downarrow\\
f^{\prime}(x): & -3x^{-4} & -2x^{-3} & -x^{-2} & \underbrace{0}_{\ast x^{-1}ではない} & 1x^0 & 2x^1
\end{array}
\]

※この規則性については『ベキ乗関数 x^2 の積分公式と抑えておきたい規則性』で解説しています。

このようにベキ乗関数の積分の規則性の中で、\(x^{-1}\) の積分だけ規則性から外れて、\(\log x\) になります。言い換えれば、\(x^{-1}\)は「実数の世界から虚数の世界への入り口」として機能しています。

\[\begin{eqnarray}
\int x^{-1}dx
&=&
\frac{1}{-1+1}x^{-1+1}\\
&=&
\frac{1}{0}x^0\\
\xrightarrow{\text{変身（虚数の世界へ？）}}
&& \log x
\end{eqnarray}\]

なぜこうなるのでしょうか。

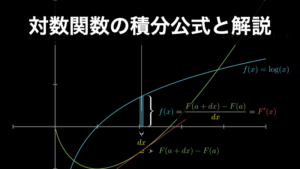
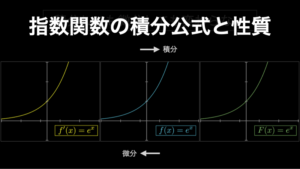
実は、これにはネイピア数 \(e\) が関わっています。『指数関数の積分公式と知っておくべき重要な２つの性質』で解説している通り、ネイピア数を底とした指数関数 \(e^x\) はすべての関数の中で唯一、積分しても微分をしても変化しない関数であり、微積分の世界で非常に特別な立ち位置にあります。

そして、この特別な関数 \(e^x\) と\(\log x\) は逆関数の関係にあります。逆関数とは、ある関数の結果を元に戻す関数です。つまり、\(e^{\log(x)}=\log(e^x)=x\) という関係にあるということです（『逆関数の微分を誰でも理解できるように視覚的に解説』解説しています）。

この特徴を活用して \(“e^{\log(x)}=x”\) とし、両辺を微分すると以下のようになります。

\[\begin{eqnarray}
e^{\log(x)} \cdot \log(x)^{\prime}
&=&
1\\
\Rightarrow
\log(x)^{\prime}
&=&
\frac{1}{e^{\log(x)}}\\
&=&
\frac{1}{x}
\end{eqnarray}\]

参照：「合成関数の微分」

これで \(\log x\) の微分が \(\frac{1}{x}\) であることが導き出されました。

そして、『積分とは何か？最もわかりやすく簡単に理解できるように解説』で解説したように、「微分積分学の基本定理」より、積分は微分の逆演算なので、同時に \(\frac{1}{x}\) の積分は \(\log x\) であるということが確定します。

以上が \(\frac{1}{x}\) の積分は \(\log x\) であることの解説です。

なお、『log（対数関数）の微分を誰でも理解できるように丁寧に解説』では、\(\log x\) の微分を、また別の観点から解説しています。併せてご覧頂くと、理解が深まりますので、ぜひご確認ください。

2. 練習問題

ここでは簡単な３つの練習問題を記しておきたいと思います。これらは暗記することを勧められる場合もありますが、ここまでの内容を理解していれば暗記する必要などなく、すぐに求められるものです。

1/1+x の積分

\(\frac{1}{1+x}\) の積分は \(\log(1+x)\) です。以下の通りです。

\[\begin{eqnarray}
\int \frac{1}{1+x}dx
&\xrightarrow{1+x \ \rightarrow \ t}&
\int \frac{1}{t}dt \\
&\xrightarrow{\int \frac{1}{x}dx=\log x}&
\log t\\
&\xrightarrow{t \ \rightarrow \ 1+x}&
\log (1+x)
\end{eqnarray}\]

1/1-x の積分

\(\frac{1}{1-x}\) の積分は \(-\log(1-x)\) です。以下の通りです。

\[\begin{eqnarray}
\int \frac{1}{1-x}dx
&\xrightarrow{1-x \ \rightarrow \ t}&
\int \frac{1}{t}(-dt) \\
&\xrightarrow{\int \frac{1}{x}dx=\log x}&
\log (-t)\\
&\xrightarrow{t \ \rightarrow \ 1-x}&
-\log (1-x)
\end{eqnarray}\]