指数関数は、微積分に重要な４つの関数（ベキ乗関数・三角関数・指数関数・対数関数）のうちの一つであり、複利金利・情報伝達・失敗情報の伝達（逆数）・蓮の葉の増殖・細胞分裂といった様々な現実世界の現象を表していることで有名です。
ここでは、この重要な指数関数の積分の公式と特徴的な２つの性質について詳しく解説します。
1. e^x の積分
まずは、底がネイピア数 \(e\) である指数関数について解説します。早速見ていきましょう。
1.1. 公式
\(e^x\) の積分公式は、以下の通りです。
指数関数の積分公式
\[\begin{eqnarray}
\int e^xdx
&=&
e^x\\
\end{eqnarray}\]
\[\begin{eqnarray}
\int e^{cx}dx
&=&
\frac{1}{c}e^{cx}
\end{eqnarray}\]
※ \(c\) は定数
試験勉強目的であれば、これらの公式を丸暗記しておけば良いです。しかし当サイトでは、現実世界の問題解決に活かせるようになることを第一の目的として解説しています。
そこで、それに役立てるために、ここで終わらずに、指数関数の微積分の性質まで確認しておくことにしましょう。
1.2. 性質
指数関数の微積分には、以下の２つの性質があります。
- 不変性
- 対称性
それぞれ解説します。なお、微分については『指数関数の微分を誰でも理解できるように解説』で詳しく解説していますので、ぜひご確認ください。
まず、指数関数 \(e^x\) は、以下の通り、微分をしても積分をしても変わりません
指数関数の性質①『不変性』
\[
\begin{array}{ccc}
e^x & \overset{\text{微分}}{\leftarrow} & e^x & \overset{\text{積分}}{\rightarrow} & e^x
\end{array}
\]
覚えやすくなるので、視覚的にも確認しておきましょう。
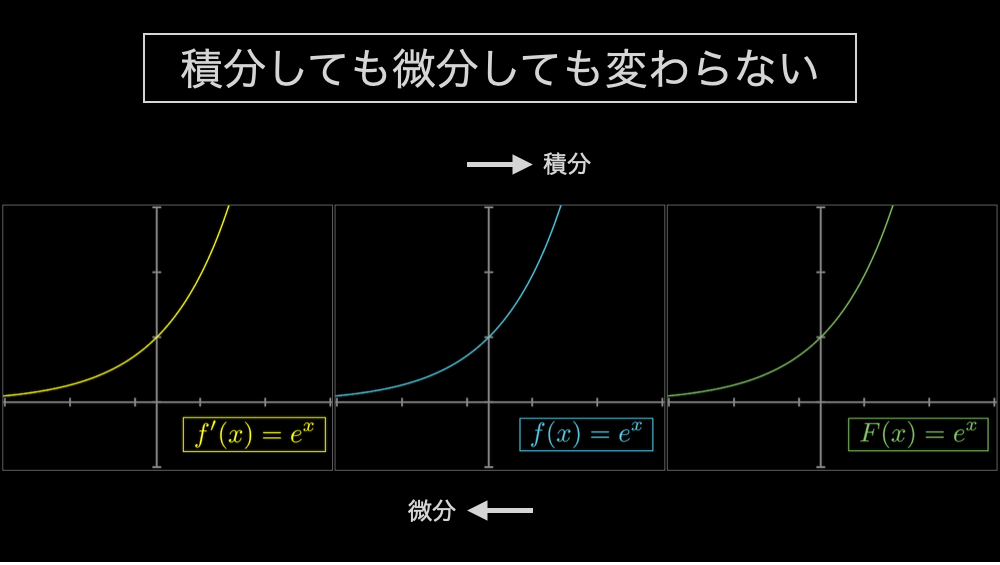
次に \(e^{cx}\) のように指数部分に定数が加わっている場合は、元の関数からは変わりますが、微分結果と積分結果は同じになります。
指数関数の微積分の性質②『対称性』
\[
\begin{array}{ccc}
-e^{-x} & \overset{\text{微分}}{\leftarrow} & e^{-x} & \overset{\text{積分}}{\rightarrow} & -e^{-x}
\end{array}
\]
これも視覚的にも確認しておきましょう。
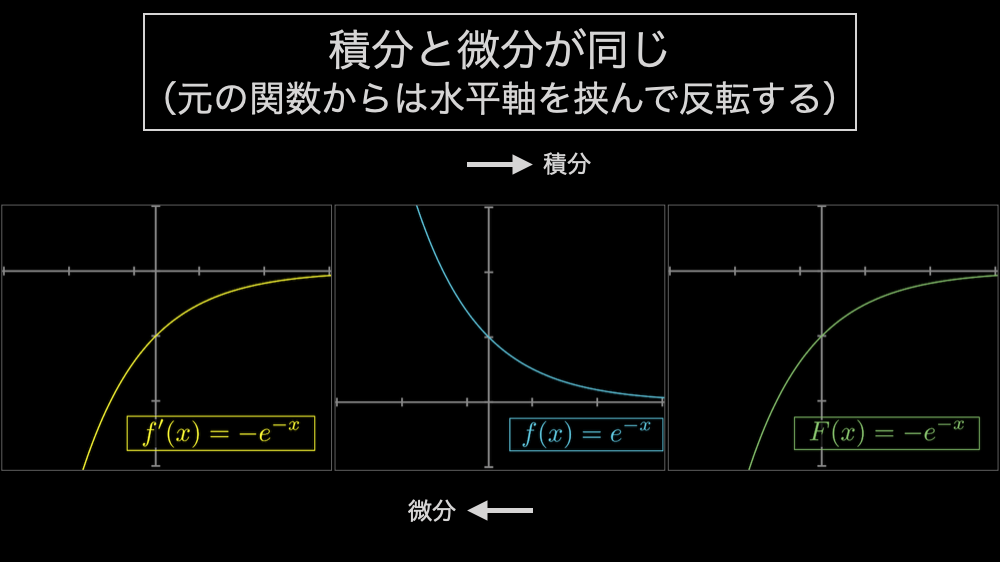
以上が指数関数の微積分の「不変性」もしくは「対称性」です。
2. a^x の積分
続いて底がネイピア数ではない指数関数 \(a^x\) の積分公式は以下の通りです。
指数関数 \(a^x\) の積分公式
\[\begin{eqnarray}
\int a^xdx
&=&
\frac{a^x}{log_ea}\\
\end{eqnarray}\]
\[\begin{eqnarray}
\int a^{cx}dx
&=&
\frac{1}{c\cdot log_ea}a^{cx}
\end{eqnarray}\]
※ \(c\) は定数
実のところ、微積分の応用（大学レベル以上）になると、\(a^x\) の形の指数関数を用いることはほとんどありません。なぜなら、指数関数の底は \(e\) で統一した方が、比較や解析がはるかにやりやすくなるからです。
そこで実際には、以下の方法で指数関数の底を \(e\) に変換して微積分を求めることになります。
指数関数の底の変換
\[\begin{eqnarray}
a^x
&=&
e^{\log_e(a)x}
\end{eqnarray}\]
こうして変換すると、上で解説した指数関数の微積分の「不変性」または「対称性」をスムーズに活用できるようになりますので、ぜひ覚えておきましょう。
3. 指数関数の積分まとめ
以上が指数関数の積分です。最後に、簡単にまとめておきましょう。
まず指数関数は、現実世界のさまざまな事象を表す重要な関数のうちの一つです。そのため、これらの微積分ができるようになると、それらの事象を分析できるようになります。
そして、指数関数の微積分には「不変性」または「対称性」という性質があります。応用する際は、これらの性質を覚えておくと、とても便利ですので、ぜひ抑えておいてください。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント