確率の求め方（計算方法）はとても簡単なのですが、公式だけを見ると、使われている言葉が難しそうで、なんだかとても難解なものに思えてしまいます。そこで、このページでは、本当は簡単なものである確率の求め方を誰でも理解できるように解説します。
それだけでなく確率を求める上で最低限知っておくべき 2 つの公式も紹介します。読み終わる頃には、確率を求めるための基礎をしっかりと身につけていることでしょう。
それでは見ていきましょう。
0. 基本用語
まずは確率を求めるために知っておきたい基本的な用語を説明しておきますので、ざっと確認しておきましょう。
- 試行：同じ状態で何度も繰り返し観測することが可能であり、その結果が偶然によって決まる行為。例えばサイコロを振るという行為。
- 事象：試行の結果として起こる出来事。例えば、サイコロを振って 1 ~ 6 の目の内のどれかが出るという出来事。
- 全事象：ある施行を行った結果、起こりうる全ての事象。慣習的に記号の U で示される。サイコロの場合は、全事象は 1 の目が出る…から 6 の目が出るまでの 6 つ。
- 根元事象：事象の最小範囲。サイコロでは、1 の目が出る、2 の目が出る、…、6 の目が出る、という個々の事象のこと。
- 空事象：決して起こらない事象のこと。慣習的に記号の φ で示される。集合論における空集合と同じ。例えば、サイコロを振ったら 0 の目が出た、という事象は起こり得ないので空事象である。
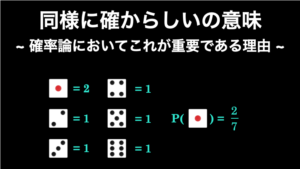
- 同様に確からしい：それぞれの根元事象が起こる頻度が同じであるということ。サイコロを振った場合、それぞれの目は同じ割合で出るとので、サイコロの出目は「同様に確からしい」。
それでは次から確率の求め方を見ていきましょう。
1. 確率の求め方
確率は、以下の方法で簡単に求めることができます。
確率の求め方
\[\begin{eqnarray}
\text{事象Aが起こる確率}
&=&
\frac{\text{事象Aが起こる場合の数}}{\text{全事象の場合の数}}\\
\Rightarrow
P(A)
&=&
\dfrac{n(A)}{n(U)}
\end{eqnarray}\]
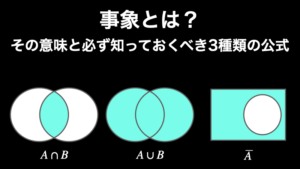
なお、「事象」についての詳しいことは『事象とは？その意味と必ず知っておくべき 3 種類の公式』で、「場合の数」についての詳しいことは『場合の数とは？ ~ 樹形図の描き方と知っておくべき 2 つの法則 ~』で解説していますので、ぜひご覧ください。
例としてサイコロの確率を考えてみましょう。
「サイコロを振る」という試行の全事象の場合の数は〈 1 ~ 6 の目が出る〉の 6 つです。その中で〈 1 の目が出る〉という事象を A とします。全事象の中で事象 A の場合の数はもちろん 1 つです（ 1 の目が 2 つあるような特殊なサイコロの場合は事象A の場合の数は 2 つということになります）。
以上のことからサイコロを振って 1 の目が出る確率は、次の通り求められます。
\[\begin{eqnarray}
\text{1の目が出る確率}
=
\frac{\text{ 1 の目が出る事象の場合の数}}{\text{全事象の場合の数}}
=
\dfrac{1}{6}
\end{eqnarray}\]
「事象」や「場合の数」などの難しそうな言葉が並んでいるので、確率は何だか高尚なもののように思えてしまうかもしれませんが、実際は小学生低学年でも求められるほど簡単なものです。
要するに確率は、起こり得ると考えられる全ての事象をリストアップして、確率を算出したい事象の数を、リストアップした全ての事象の数で割るという方法で求めることができます。
2. 最低限抑えておくべき2つの公式
ここでは確率の計算の基本として、最低限抑えておくべき公式を解説しておきます。それは以下の 2 つです。
- 乗法定理：異なる複数の事象が続けて起こる確率を求める
- 加法定理：異なる複数の事象のうち少なくとも 1 つ以上が起こる確率を求める
それぞれ見ていきましょう。なお、ここの内容は『集合とは？覚えておくべき 6 つの記号と 1 つの法則』を読んでおくと遥かにわかりやすくなりますので、ぜひ併せてご覧ください。
2.1. 乗法定理
これは異なる複数の事象が続けて起こる確率を求めるための定理です。要するに A の後に B が起こる確率です。以下のように求めます。
確率の乗法定理
\[\begin{eqnarray}
\text{事象 A の後に B が起こる確率}
&=&
\text{事象 A が起こる確率}
\times
\text{事象 B が起こる確率}\\
\end{eqnarray}\]
\[\begin{eqnarray}
\Rightarrow
P(A \cap B)
&=&
P(A)
\times
P(B)
\end{eqnarray}\]
例として、1 つのサイコロを 2 回振ったときに、2 回続けて 1 の目が出る確率はどうなるでしょうか。まず最初の試行で 1 の目が出る確率は 1 / 6 です。そして次の試行で 1 の目が出る確率も 1 / 6 です。そのため、次のように計算できます。
\[\begin{eqnarray}
\text{ 1 の目が 2 回続けて出る確率}
&=&
\text{ 1 の目が出る確率}
\times
\text{ 1 の目が出る確率}\\
&=&
\dfrac{1}{6}
\times
\dfrac{1}{6}
=\dfrac{1}{36}
\end{eqnarray}\]
この定理は対象となる事象の数がどれだけあっても変わりません。例えば 1 の目が 5 回続けて出る確率はどうなるでしょうか。次のようになります。
\[\begin{eqnarray}
\text{ 1 の目が 5 回続けて出る確率}
&=&
\dfrac{1}{6}
\times
\dfrac{1}{6}
\times
\dfrac{1}{6}
\times
\dfrac{1}{6}
\times
\dfrac{1}{6}\\
&=&
\dfrac{1}{7776}
\end{eqnarray}\]
以上が確率の乗法定理です。
2.2. 加法定理
確率の加法定理は、複数の事象のうち少なくとも 1 つ以上が起こる確率を求めるためのものです。要するに事象 A と B があるとき、〈A が起こる、またはBが起こる、または A と B が起こる〉という場合を全てひっくるめた確率です。これは以下の方法で求められます。
確率の加法定理
\[\begin{eqnarray}
\text{事象 A と B のうち 1 つ以上が起こる確率}
&=&
\text{事象 A が起こる確率}
+
\text{事象 B が起こる確率}
–
\text{事象 A の後に B が起こる確率}
\end{eqnarray}\]
\[\begin{eqnarray}
\Rightarrow
P(A \cup B)
&=&
P(A)
+
P(B)
–
P(A \cap B)
\end{eqnarray}\]
たとえば 1 組 52 枚のトランプから 1 枚を取り出すとします。このとき数字の 2 が出る事象を A、スートのハートが出る事象を B とすると、A または B が起こる確率（A が起こる、または B が起こる、または A と B が起こる確率）はどうなるでしょうか。
まず 1 組 52 枚のトランプの中に同じ数字を持つカードは 4 枚ありますから、事象 A が起こる確率は 4 / 52 です。そして同じスートのカードは 13 枚ありますから、事象 B が起こる確率は 13 / 52 です。これらの確率を足すと 4 / 52 + 13 / 52 = 17 / 52 になります。しかし、これはまだ答えではありません。なぜなら、この 17 / 52 という数字の中には、A と B が同時に起こる確率（ハートの 2 を取り出す確率）が二重に含まれているからです。
そこで正しい確率を求めるには、A と B が同時に起こる確率を引いてやらなければいけません。そして、これは既に見た乗法定理より 4 / 52 × 13 / 52 = 1 / 52 と求められます。
以上のことから A または B が起こる確率は以下の通りとなります。
\[\begin{eqnarray}
\text{ 2 またはエースを引く確率}
&=&
\text{ 2 を引く確率}
+
\text{エースを引く確率}
–
\text{エースの 2 を引く確率}\\
&=&
\dfrac{4}{52}
+
\dfrac{13}{52}
–
\dfrac{1}{52}\\
&=&
\dfrac{16}{52}
\end{eqnarray}\]
以上が確率の加法定理です。
3. 練習問題
それでは最後に基本的な問題を解いておきましょう。
問題
次の確率を求めましょう。
- (1) 2 個のサイコロを振って、2 つとも偶数の目が出る確率
- (2) 2 個のサイコロを振って、2 つとも偶数の目が出る、またはどちらも素数の目が出る確率
- (3) 2 個のサイコロを振って、少なくとも一方で偶数の目が出る確率
(1) 2 つとも偶数の目が出る確率
これは乗法定理を使います。サイコロを振って偶数の目が出る確率は 3 / 6 なので、次の通りになります。
\[\begin{eqnarray}
&&
\text{偶数が出る確率}
\times
\text{偶数が出る確率}
&=&
\dfrac{3}{6}
\times
\dfrac{3}{6}
=
\dfrac{9}{36}
=
\dfrac{1}{4}
\end{eqnarray}\]
(2) 2 つとも偶数の目が出る、または 2 つとも素数の目が出る確率
これは加法定理で解きます。まず 2 つとも偶数の目が出る確率は上で求めた通り 1 / 4 です。そしてサイコロの目の中で素数は 2, 3, 5 の 3 つなので、2 つとも素数の目が出る確率も 1 / 4 になります。そして 2 は素数でもあり偶数でもあるので、2 つとも 2 の目が出る確率も求める必要があります。そして、その確率は当然 1 / 6 × 1 / 6 = 1 / 36 です。
以上のことから次のように求められます。
\[\begin{eqnarray}
&2&
つとも偶数の目が出る確率
+
\text{2 つとも素数の目が出る確率}
–
\text{2 つともの 2 の目が出る確率}
\\
&=&
\dfrac{1}{4}
+
\dfrac{1}{4}
–
\dfrac{1}{36}
=
\dfrac{17}{36}
\end{eqnarray}\]
(3) 2 個のサイコロを振って、少なくとも一方で偶数の目が出る確率
上では解説していないので反則気味なのですが、実は、この問題を解くには「余事象」について理解しておく必要があります。詳しくは『余事象とは？確率計算で必ず覚えておくべき重要な 1 つの法則』で解説しています。
そしてこの問題は以下のように解くことができます。
\[\begin{eqnarray}
&&
1
–
[
\text{偶数の目が出ない確率}
\times
\text{偶数の目が出ない確率}
]
\\
&=&
1-[
\dfrac{3}{6}
\times
\dfrac{3}{6}
]
=
\dfrac{27}{36}
=
\dfrac{3}{4}
\end{eqnarray}\]
4. まとめ
以上が確率の求め方です。いきなり公式を見ると、確率って何だか難しそうなものに見えるかもしれません。
しかし、実際には小学校低学年でも求められるほど単純で、①起こり得ると考えられる全ての事象をリストアップして、②確率を算出したい事象の数を、リストアップした全ての事象の数で割る、ということを行うだけです。この点はぜひ覚えておいてください。
また、乗法定理や加法定理もシンプルに考えるととても簡単です。事象 A と B が連続して起こる確率は、それぞれの事象の確率の積になります。そして、事象 A または 事象 B が起こる確率は、A の確率と B の確率の和から、A と B が連続して起こる確率を引いたものになります。これについては集合論を理解しておくと、当たり前のように納得できるでしょう。
ぜひ参考にして頂ければと思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント