Generator.standard_tは、標準t分布(スチューデントのt分布)から乱数配列を生成するジェネレータメソッドです。
t分布は、双曲線分布の特別なケースです。自由度が大きくなるほど、標準正規分布に近づいていきます。標準正規分布については以下のページで解説しています。
t検定は、データが正規分布のものであるという仮定に基づいており、標本の平均が実際の平均に対する精度の高い予測となっているかを検証することができます。
このページでは標準t分布から乱数配列を生成するGenerator.standard_tについて解説します。
1. 書式
書き方:
Generator.standard_t(df, size=None)
パラメーター:
| df: float or array_like of floats 自由度(>0) |
| size: int or tuple of ints, optional 出力する配列のshape。(m, n, k)を渡すと、shape(m, n, k)の乱数配列を生成する。デフォルト値Noneで、dfがスカラーの場合は1つの乱数の値を返す。それ以外の場合はnp.array(df).sizeの乱数配列を返す。 |
戻り値:
| out: ndarray or scalar パラメータを設定した標準t分布から乱数配列を生成。 |
Notes
標準t分布の確率密度関数は次の通りです。
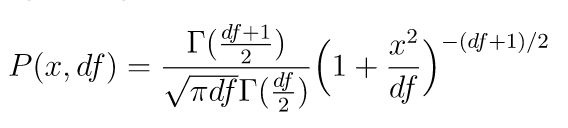
2. サンプルコード
それでは、サンプルコードを見ていきましょう。
まずは、random.default_rng コンストラクタでジェネレータオブジェクトを作成します。『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』に目を通しておいてください。
import numpy as np
rng = np.random.default_rng()
rng
こうして作成したジェネレータオブジェクト rng に対して、Generator.standard_tを呼び出すことによって、標準t分布から乱数配列を取得することができます。
第一引数にdf(自由度)、第二引数にsizeを渡します。
rng.standard_t(10, 5)
応用例
11人の女性の1日当たりのエネルギー摂取量(kJ)が以下の通りだったとします。
intake = np.array([5260., 5470, 5640, 6180, 6390, \
6515, 6805, 7515, 7515, 8230, 8770])
彼女たちのエネルギーの摂取量は、推奨摂取量の7725kJから逸脱しているでしょうか。
ここでは自由度10とします。標本の平均は推奨摂取量の95%側に位置するでしょうか。
s = rng.standard_t(10, size=100000)
np.mean(intake)
intake.std(ddof=1)
t統計量の計算のために、ddofパラメータを不偏値に設定します。つまり、標準偏差の除数が自由度N-1になります。
t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake)))
import matplotlib.pyplot as plt
h = plt.hist(s, bins=100, density=True)
片側t検定において、t統計量は分布の中でどこまで離れているでしょうか。
np.sum(s<t) / float(len(s))
結果、p値は約0.009でした。つまり、帰無仮説は99%の確率で真であるということです。
3. まとめ
以上のように、Generator.standard_tは、t分布から乱数配列を生成するジェネレータメソッドです。
以前は、numpy.random.standard_t関数が使われていましたが、ジェネレータメソッドを使うようにしましょう。こちらの方が、処理が高速で、大量のデータを扱う科学技術計算に適しているからです。

コメント