ベクトルのスカラー倍

線形代数においてベクトルのスカラー倍は、もっとも基本的な演算の一つです。このページではベクトルのスカラー倍について以下のことを解説します。

ベクトルのスカラー倍とは

「ベクトルとは」では、プログラマーにとってベクトルはデータであり数値のリストであるということを解説しました。物理学や数学ではベクトルは「長さと向きをもつ矢印」であると考えますが、データサイエンスにおいては単なるデータです。

これ以上でも以下でもありません。

そのため物理学や数学では、ベクトルのスカラー倍は 、1 つの矢印を伸縮したり反転したりするものですが、プログラマーは基本的にそのように幾何学的に考えることはありません。

私たちプログラマーにとってベクトルのスカラー倍とは、「機械学習のためのデータの準備などの何らかの目的で、あるベクトル（データ）に数値（スカラー）を掛けることで、新しいベクトル（データ）を作る手段」に過ぎないのです。

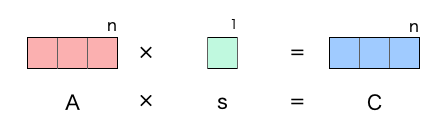
以上がプログラマーにとってのベクトルのスカラー倍です。

ベクトルのスカラー倍のやり方

ベクトルのスカラー倍は非常に簡単です。以下の通り、単純にベクトルの一つひとつの要素に、スカラー \(s\) を掛けるだけです。

\[
as=
\begin{pmatrix}
s \times a_1 &
s \times a_2 &
s \times a_3
\end{pmatrix}
\]

たとえば次のようになります。

\[\begin{eqnarray}
a&=&
\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}\\
S&=&
2\\
2a &=&
\begin{pmatrix}
2 & 4 & 6
\end{pmatrix}
\end{eqnarray}\]

Pythonでベクトルのスカラー倍

NumPy では * 演算子で求められます。

# NumPy のインポート
import numpy as np

# 1つ目のベクトルの定義
a = np.array([1, 2, 3])
print(a)

[1 2 3]

# スカラーを定義
s = 2
print(s)

2

# ベクトルのスカラー倍
c = a * s
print(c)

[2 4 6]