行列の割り算とは何か

「行列とは」で述べた通り、行列はベクトルを変換するための写像（関数）です。そして行列のスカラー倍は、何らかの目的で、対象の関数の効き具合を \(s\) 倍するというものです。これも \(\cdot\) 演算子を使って表記します。

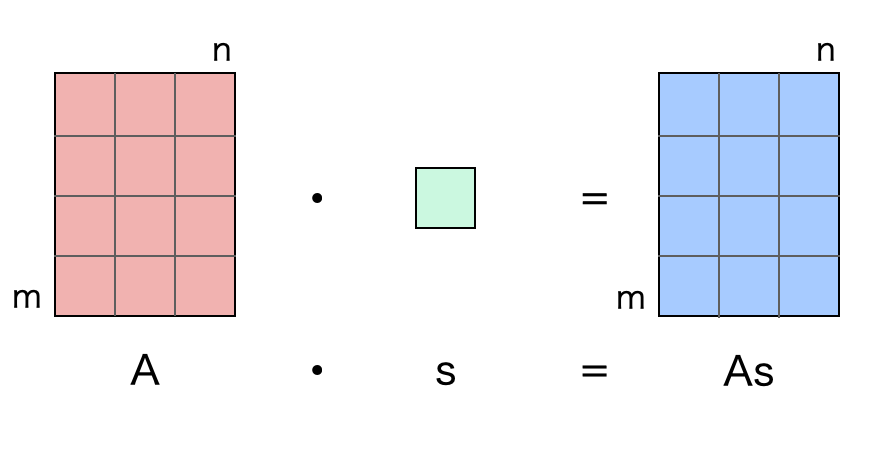
以上が行列のスカラー倍です。

行列のスカラー倍のやり方

行列のスカラー倍の計算結果は行列のそれぞれの要素がスカラー倍されたものになります。

\[\begin{eqnarray}
A=
\begin{pmatrix}
a_{1,1}
&
a_{1,2}\\
a_{2,1}
&
a_{2,2}\\
a_{3,1}
&
a_{3,2}
\end{pmatrix}
\end{eqnarray}\]

\[\begin{eqnarray}
A \cdot s=
\begin{pmatrix}
a_{1,1} \times s
&
a_{1,2} \times s\\
a_{2,1} \times s
&
a_{2,2} \times s \\
a_{3,1} \times s
&
a_{3,2} \times s
\end{pmatrix}
\end{eqnarray}\]

例えば次のようになります。

\[\begin{eqnarray}
2
\cdot
\begin{pmatrix}
1
&
2\\
3
&
4\\
5
&
6
\end{pmatrix}
=
\begin{pmatrix}
2
&
4\\
6
&
8\\
10
&
12
\end{pmatrix}
\end{eqnarray}\]

Pythonで行列のスカラー倍

Python では NumPy の配列とスカラーを * 演算子でつなぐことで求められます。

In [1]:

# NumPy のインポート
import numpy as np

# 行列の定義
A = np.array([[1,2],[3,4],[5,6]])
print(A)

[[1 2]
 [3 4]
 [5 6]]

In [2]:

# スカラーの定義
b = 2
print(b)

In [3]:

# 行列とスカラーの積
C = A * b
print(C)

[[ 2  4]
 [ 6  8]
 [10 12]]

プログラマーのための線形代数

行列の割り算とは何か

行列のスカラー倍のやり方

Pythonで行列のスカラー倍