行列の掛け算(アダマール積)は、もう一つのドット積よりは使用頻度は低いですが、線形代数において基本的な行列の演算の一つです。当ページでは、これについて以下のことがわかります。
このページでわかること
- 行列の掛け算(アダマール積)とは何か
- 行列の掛け算(アダマール積)のやり方
- Python で行列の掛け算(アダマール積)
行列の掛け算(アダマール積)とは何か
「行列とは」で述べた通り、行列はベクトルを変換するための写像(関数)です。そして行列のアダマール積は、何らかの目的で 2 つの関数で掛け算を行なって、新しい 3 つ目の関数を作るということを意味します。
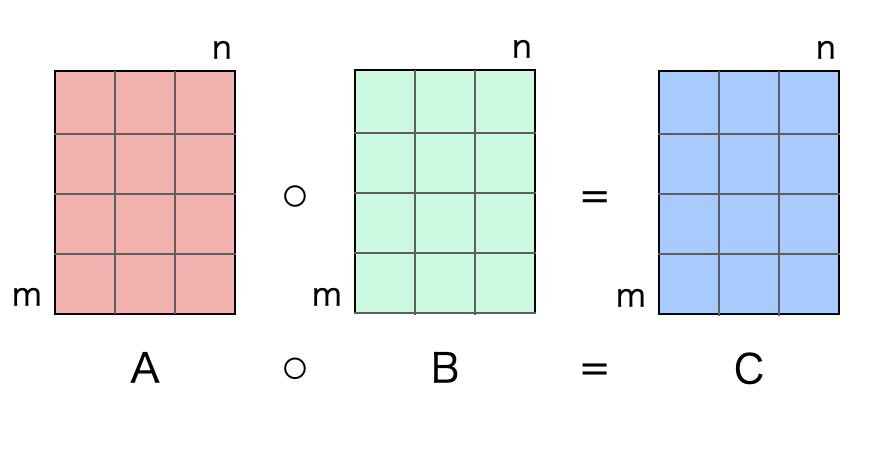
以上が行列のアダマール積です。
行列の掛け算(アダマール積)のやり方
行列のアダマール積は簡単です。以下の 2 つの行列があるとします。
\[\begin{eqnarray}
A=
\begin{pmatrix}
a_{1,1} & a_{1,2}\\
a_{2,1} & a_{2,2}
\end{pmatrix}, \ \ \
B=
\begin{pmatrix}
b_{1,1} & b_{1,2}\\
b_{2,1} & b_{2,2}
\end{pmatrix}
\end{eqnarray}\]
これらの行列同士でアダマール積を行うと、それぞれ同じ要素の値で掛け算が行われます。
\[\begin{eqnarray}
A \circ B=
\begin{pmatrix}
a_{1,1} \times b_{1,1}
&
a_{1,2} \times b_{1,2}\\
a_{2,1} \times b_{2,1}
&
a_{2,2} \times b_{2,2}\\
\end{pmatrix}
\end{eqnarray}\]
例として次の 2 つの行列のアダマール積を求めてみましょう。
\[\begin{eqnarray}
A=
\begin{pmatrix}
5 & 6\\
7 & 8
\end{pmatrix}, \ \ \
B=
\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}
\end{eqnarray}\]
これらの行列同士でアダマール積を行うと、それぞれ同じ要素の値が掛け合わされます。
\[\begin{eqnarray}
A \circ B=
\begin{pmatrix}
5 & 12\\
21 & 32\\
\end{pmatrix}
\end{eqnarray}\]
なお行列のアダマール積は、2 つの行列の行数と列数が同じである場合のみ可能です。
Pythonで行列の掛け算(アダマール積)
Python では NumPy で作成した行列同士を * 演算子で繋ぐことでアダマール積を求めることができます。
# NumPy のインポート
import numpy as np
# 1 つ目の行列の定義
A = np.array([[1,2,3],[4,5,6]])
print(A)
# 2 つ目の行列の定義
B = np.array([[1,2,3],[4,5,6]])
print(B)
# 行列の掛け算(アダマール積)
C = A * B
print(C)