積の微分公式を誰でも直観的に理解できるように解説

積の微分公式は、関数の積の微分を求められる公式です。このページでは、これについて誰でも理解できるように解説していきます。具体的には以下の３点について深く理解できるようになります。

• 関数の積の簡単なおさらいできる
• 積の微分公式を暗記に頼らずに直観的に覚えられるようになる
• 積の微分公式の証明を数式だけでなく視覚的なイメージで理解できるようになる

それでは早速始めましょう。

1. 関数の積とは

最初に関数の積について軽く解説しておきます。

\(f(x)\) と \(g(x)\) という２つの関数があるとき、これらの関数を掛け合わせた \(f(x)g(x)\) が関数の積です。たとえば \(f(x)=\sin(x), \ g(x)=x^2\) としたら、\(f(x)g(x)=\sin(x)x^2\) です。

参考までに、これらをグラフに描いたら、下図のような曲線になります。

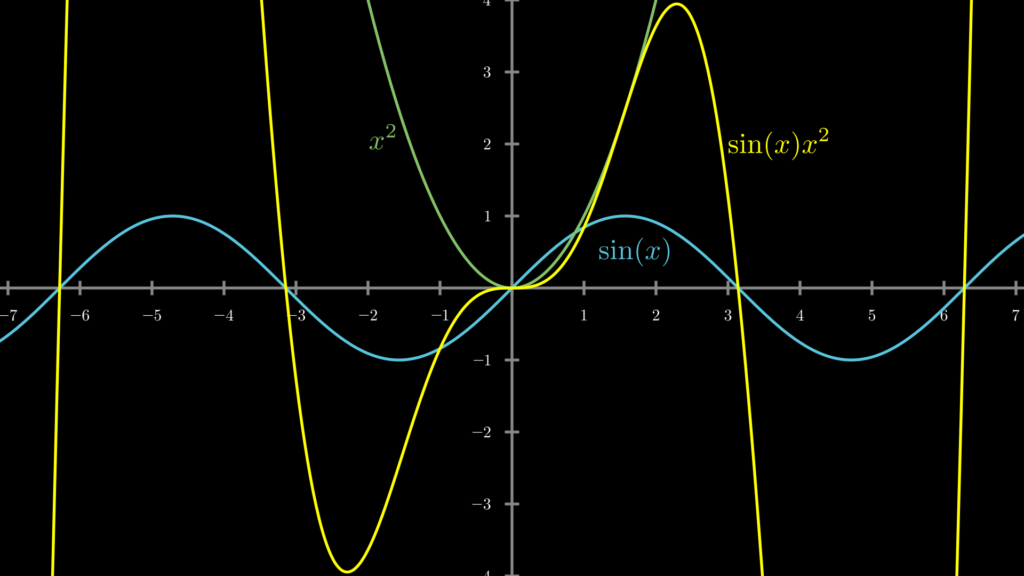
このように関数の積は、単純な関数と比べて複雑な曲線を描きます。それでは、この関数の積の微分はどのように求めることができるのでしょうか。

2. 関数の積の微分公式

結論からお伝えすると、関数の積の微分は以下の公式で求めることができます。

どのような関数の組み合わせだったとしても、必ずこの公式の通りになります。これを「積の微分公式 “product rule”」と言います。

例として、上で用いた \(f(x)g(x)=\sin(x)x^2\) の微分を求めたものが以下の計算です。なお、\(\sin(x)\) の微分が \(\cos(x)\) になることについては『sinの微分はなぜcos？誰でも直観的に理解できるように解説』で解説しています。

この導関数をグラフに描いてみたもの下図です。

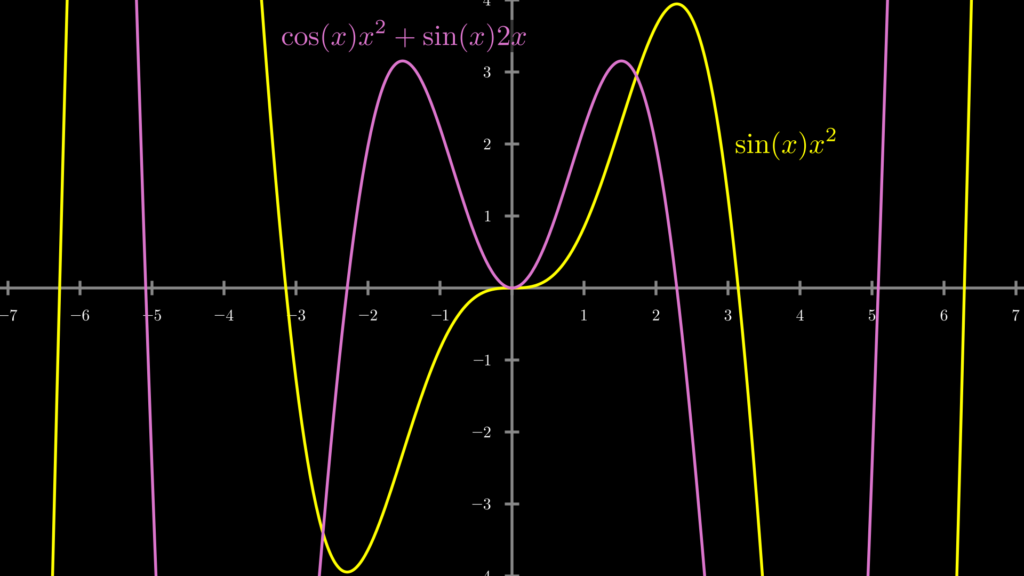
3. 積の微分公式の証明

それでは、なぜ関数の積の微分は、この公式で求めることができるのでしょうか。

関数の積の微分なので、単純に２つの関数の微分を \(f^{\prime}(x)g^{\prime}(x)\) と掛け合わせて求められそうに思ってしまいます。しかし、微分の世界と一般的な算数の世界は、異なるものです。そのため、最初は多くの人が混乱してしまいそうになっています。

ただし、微分の考え方に触れていけば、一般的な算数の世界は誰もが直観的に理解しているように、微分の世界についても誰でも直観的に理解できるようになります。そうなれば、算数の積と同じぐらい積の微分も当たり前になります。

そして、ここではまさに、そのように直観的に理解できるように、積の微分公式を視覚的に証明していきます。ぜひ、楽しみながら読み進めて頂ければと思います。

なお、引き続き \(f(x)=\sin(x),\ g(x)=x^2\) として、これらの関数の積 \(f(x)g(x)=\sin(x)x^2\) を見ていくことにします。

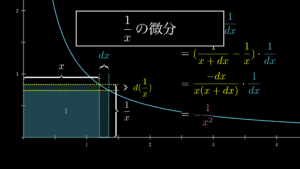
3.1. 関数の積は四角形の面積

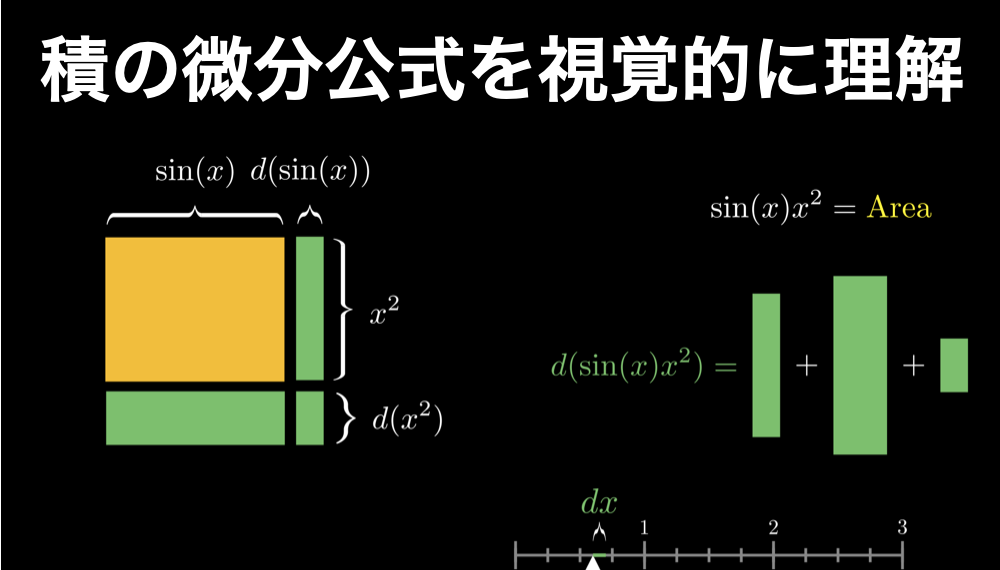
微分学に限らず、何らかの積を直観的に理解できるようになるための鉄板のコツがあります。そのコツとは、積を四角形の面積としてイメージすることです。つまり、\(\sin(x)x^2\)を一方の辺の長さが\(\sin(x)\)で、他方の辺の長さが \(x^2\) の四角形の面積として捉えるのです。

そして、この四角形の辺はどちらも x の関数なので、当然、この四角形の面積は \(x\) の値によって変化することになります。

これは以下のアニメーションをご覧頂くと、視覚的に把握することができますので、ぜひご確認ください。

このように視覚的にイメージできると、数学的な応用力や想像力がどんどん向上していきますので、ぜひともイメージ力を鍛えていきましょう。

3.2. 四角形の面積の変化量を求める

関数の積を四角形の面積として捉えると、関数の積の微分は、この面積の瞬間変化率であるとイメージすることができます。

この辺りの理解が曖昧な方は、ぜひ『微分とは何か？わかりやすくイメージで解説』をもう一度ご確認ください。

さて、それでは、この面積の変化量はどのように求めることができるのでしょうか。早速、以下のアニメーションをご覧ください。

このように面積の変化量は、３つの長方形の面積の合計で求めることができます。

さて、分かりやすくするために、アニメーションの中では \(dx\) の値を大きく取っています。しかし、実際は \(dx\) は限りなく \(0\) に近い値です。そのため、３つの四角形のうち、一番小さなものは、他の２つと比べて、考慮の必要がないほど小さな数になり、実際には無視することができます（この点については『べき乗（累乗）の微分公式-誰でも必ず深く理解できるように解説-』を読み直していただくと、簡単に理解することができます）。

以上のことから面積の変化量は以下の式で求められることになります。

3.3. 四角形の面積の変化率

あとは、この面積の変化量 \(d(\sin(x)x^2)\) を \(x\) の変化量である \(dx\) で割ることで、この面積の瞬間の変化率（=関数の積の微分）を求めることができますね。

これを計算したものが以下です。

このように公式通りの答えが求められることを確認できます。

なお２段目の式について補足しておきます。公式より \(\sin(x)\) の微分は \(\cos(x)\) ですが、これは分解すると \(\frac{d(\sin(x))}{dx}=\frac{\cos(x)dx}{dx}=\cos(x)\) というようになっています。同じように \(\frac{d(x^2)}{dx}=\frac{2xds}{dx}=2x\) となっています。これについては、『べき乗（累乗）の微分公式-誰でも必ず深く理解できるように解説-』を見返して頂くと、数式を介さなくても直感的にわかるようになります。微分とは、分子のうち\(dx\) が１回だけ掛かっている部分と、分母の \(dx\) の割り算なのです。

さて、\(f(x)=\sin(x), \ g(x)=x^2\) として見てきましたが、これを一般化して書き直したものが以下の証明式です。

この公式はどのような関数の組み合わせでも同じです。

4. 積の微分公式のまとめ

以上が積の微分公式です。

ここまで解説してきたように、関数の積を四角形の面積として捉えることで、なぜ積の微分が、\(f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\) になるのかが分かるようになります。

そして、こうしたイメージ方法に慣れれば、通常の算数の積算と同じように、微分の積も当たり前のものになっていきます。

当ページが、そのための役に立ったならとても嬉しく思います。