逆三角関数は、三角関数と同じように工学・物理学・幾何学などなどで幅広く使われる重要な関数です。そこで、当ページでは、この逆三角関数の微分について詳しく解説していきます。
具体的には以下のことがわかります。
- 逆三角関数とは何か（性質と三角関数との関係）
- 逆三角関数の微分公式
- 逆三角関数の微分の簡単な求め方
ぜひ参考になればと思います。
なお逆三角関数の微分を理解するためには、それぞれの三角関数と、逆関数の微分の理解が必要です。これらの理解に不安がある方は、以下のページでしっかりと理解しておきましょう。
それでは始めましょう。
1. 逆三角関数とは
まずは逆三角関数とは何かを簡単におさらいしておきましょう。ここの内容は、逆三角関数の微分を理解する上で必須のものです。
1.1. ３つの逆三角関数
逆三角関数は、文字通り、三角関数の逆関数です。主に以下の３つがあります。
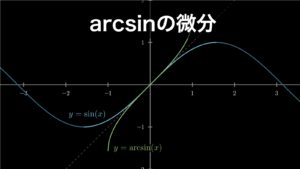
- arcsin
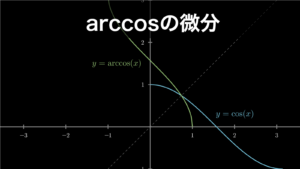
- arccos
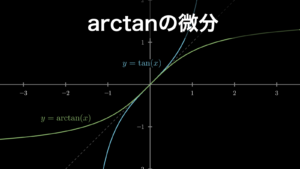
- arctan
それぞれ以下のような曲線を描きます。
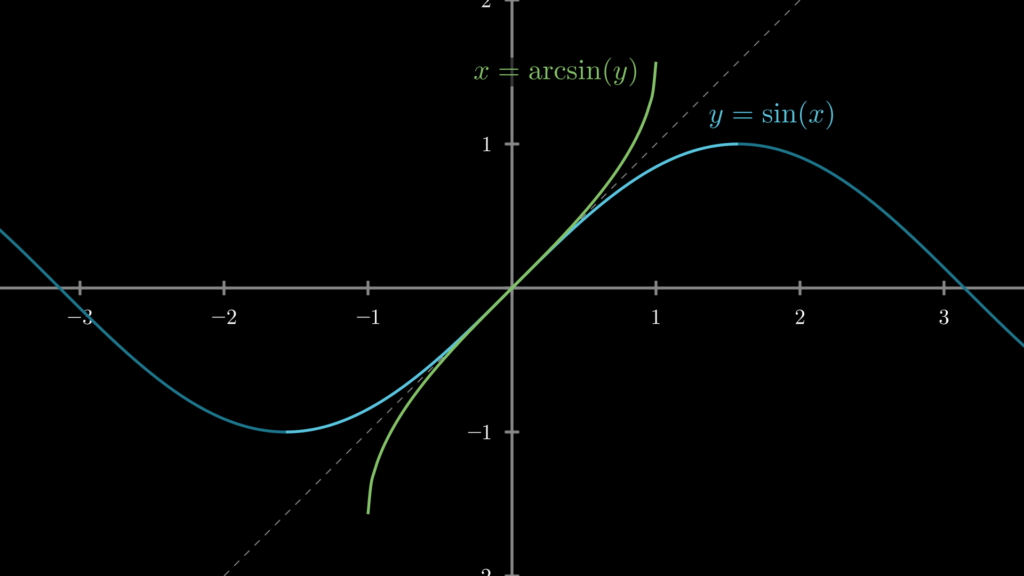
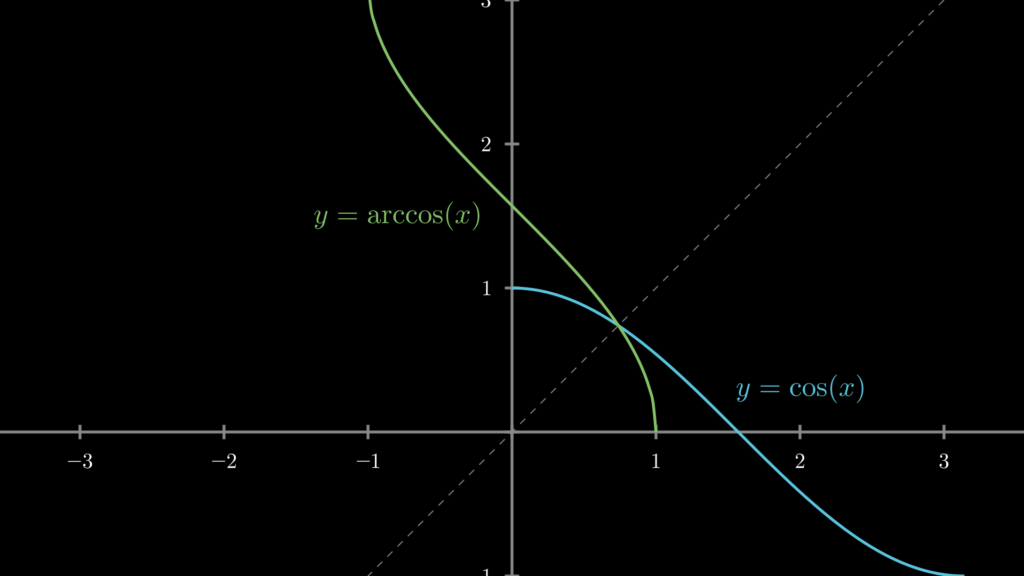
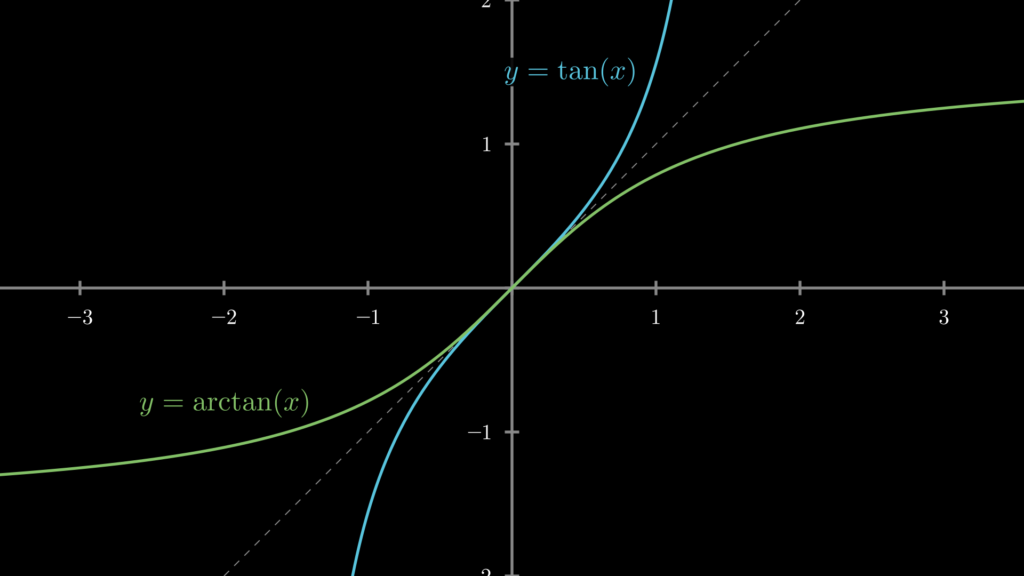
なお、これらの逆関数は、それぞれ sin^-1・cos^-1・tan^-1 と表記されることもあります。ただし、この表記方法ではべき乗なのか逆関数なのかが理解しづらくなってしまうため、基本的には arc をつけた表記の方が好ましいでしょう。
また、逆三角関数には他にも arccot・arcsec・arccsc がありますが、まずは上の３つを理解することが大切です。これらを理解していれば、その応用で他のものも簡単に理解できるようになります。
1.2. 逆三角関数とは具体的には何か
さて、それでは逆三角関数は具体的にはどのような関数なのでしょうか。
まず逆関数とは、\(y=f(x)\) に対して \(x=g(y)\) となる関数のことでしたね。つまり、逆関数は関数の値を元に戻すものであるということです。そのため \(g(f(x))=f(g(x))=x\) になります。これが逆関数の性質です。
三角関数の逆関数である逆三角関数もこれと同じです。\(\arcsin\) に \(\sin(\theta)\) の値を、\(\arccos\) に \(\cos(\theta)\) の値を、\(\arctan\) に \(\tan(\theta)\) の値を入力すると、それぞれの \(\theta\) をラジアンで出力します。以下に示している通りです。
逆三角関数は三角関数の値から \(\theta\) を求める関数
- \(\arcsin(\sin(\theta)) = \sin(\arcsin(\theta)) = \theta\) ※(\(-\pi/2<\theta<\pi/2\))
- \(\arccos(\cos(\theta)) = \cos(\arccos(\theta)) = \theta\) ※(\(0<\theta<\pi\))
- \(\arctan(\tan(\theta)) = \tan(\arctan(\theta)) = \theta\) ※(\(-\pi/2<\theta<\pi/2\))
1.3. 逆三角関数と三角関数の関係
もう一つ重要な点として、逆三角関数と、それぞれの三角関数は以下のような関係にあるということを理解しておきましょう。
arcsinと三角関数
まず、arcsin の値を三角関数に入力すると次の値が出力されます。
arcsin と三角関数の関係
- \(\sin(\arcsin (x))=x\)
- \(\cos(\arcsin (x))=\sqrt{1-x^2}\)
- \(\tan(\arcsin (x))=\dfrac{x}{\sqrt{1-x^2}}\)
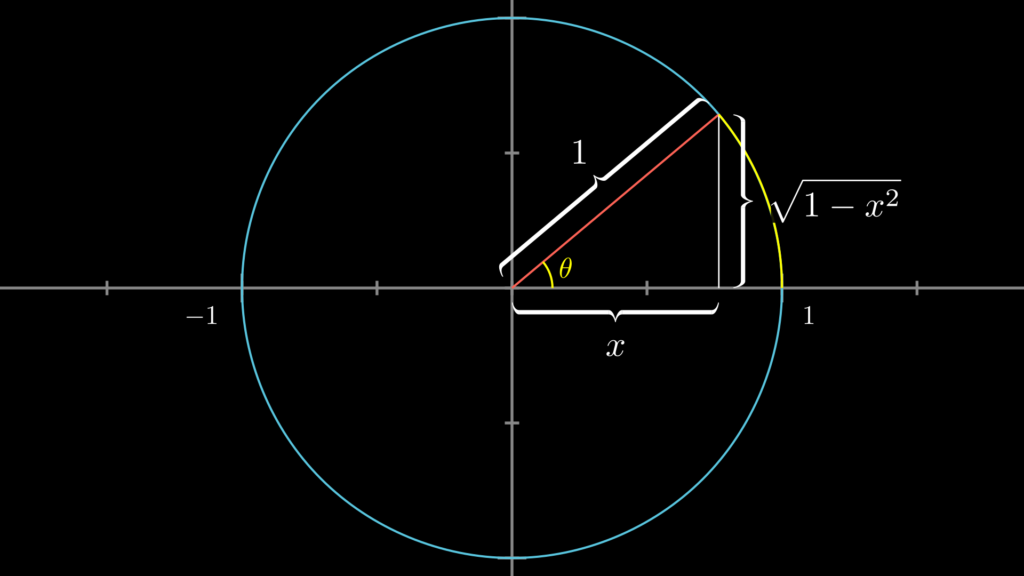
これは以下のように \(\sin(\theta)=x\) とする単位円上の直角三角形をイメージすると、簡単に求められるようになります（隣辺は三平方の定理から求められます）。
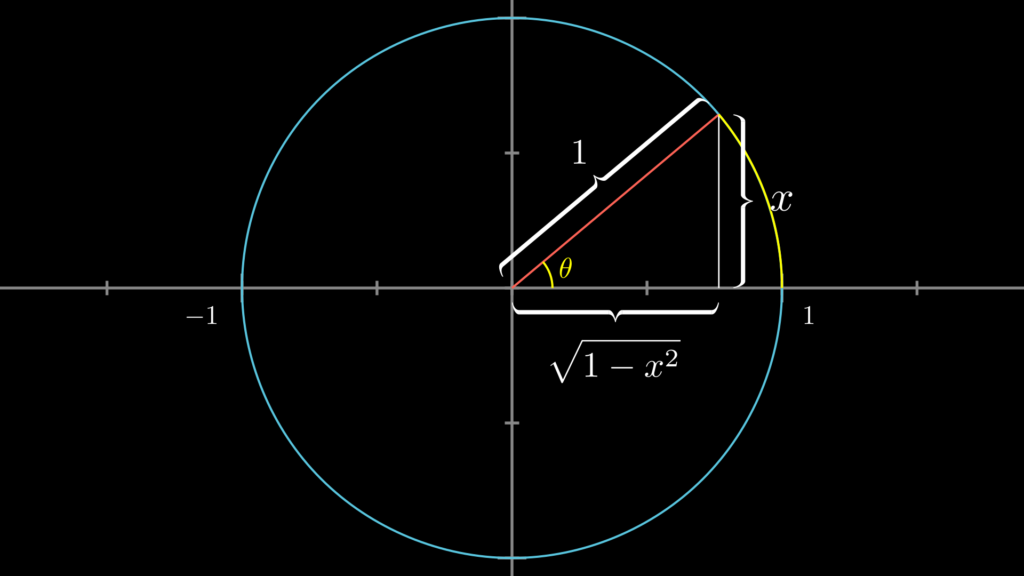
arccosと三角関数
arccos の値を三角関数に入力すると次の値が出力されます。
arccos と三角関数の関係
- \(\cos(\arccos (x))=x\)
- \(\sin(\arccos (x))=\sqrt{1-x^2}\)
- \(\tan(\arccos (x))=\dfrac{\sqrt{1-x^2}}{x}\)
これは \(\cos(\theta)=x\) とする単位円上の直角三角形をイメージすると、簡単に求められるようになります（対辺は三平方の定理から求められます）。
arctanと三角関数
arctan の値を三角関数に入力すると次の値が出力されます。
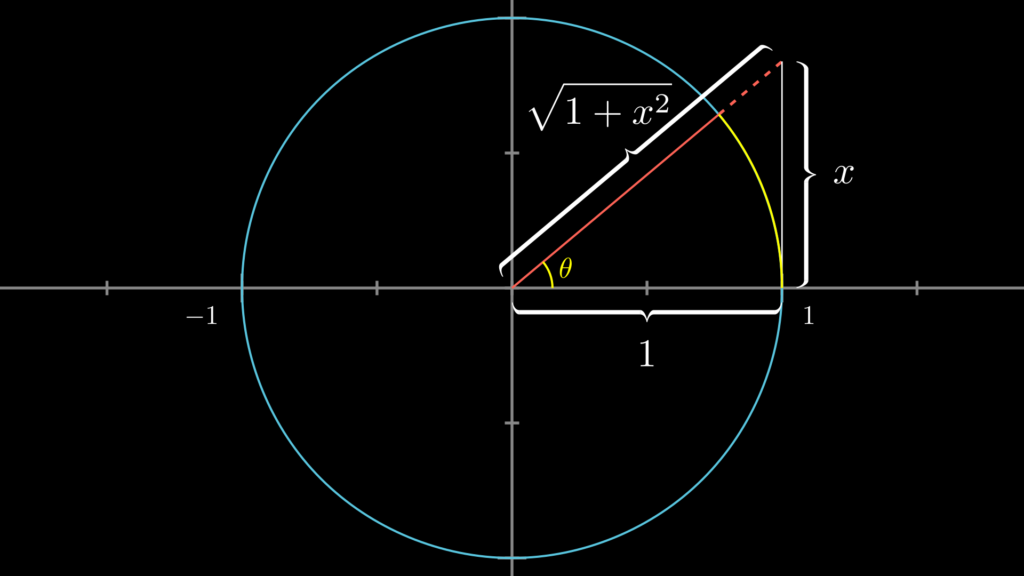
arctan と三角関数の関係
- \(\tan(\arctan (x))=x\)
- \(\cos(\arctan (x))=\dfrac{1}{\sqrt{1+x^2}}\)
- \(\sin(\arctan (x))=\dfrac{x}{\sqrt{1+x^2}}\)
これは \(\tan(\theta)=x\) とする単位円上の直角三角形をイメージすると、簡単に求められるようになります（斜辺は三平方の定理から求められます）。
以上が逆三角関数です。
2. 逆三角関数の微分
さて、それでは逆関数の微分はどうなるのでしょうか。答えからお伝えすると、以下の通りになります。
逆三角関数の微分
\[
\arcsin^{\prime}(x)=\dfrac{1}{\sqrt{1-x^2}}
\]
\[
\arccos^{\prime}(x)=-\dfrac{1}{\sqrt{1-x^2}}
\]
\[
\arctan^{\prime}(x)=\dfrac{1}{1+x^2}
\]
なぜ、このようになるのでしょうか。一つずつ見ていきましょう。
2.1. arcsin (sin^-1) の微分
arcsin は sin の逆関数です。そのため、\(y=\sin(x)\)、\(x=\arcsin(y)\) となります。このことから arcsin の微分は、逆関数の微分公式を使って sin から求めることができます。
以下の通りです。
arcsin の微分の証明（逆関数の微分公式より）
\[\begin{eqnarray}
\arcsin^{\prime}(y)
&=&
\dfrac{1}{\sin^{\prime}(x)}\\
&=&
\dfrac{1}{\cos(x)}\\
\end{eqnarray}\]
これは \(\arcsin^{\prime}(y)=\arcsin^{\prime}(\sin(x))\) なので \(\arcsin^{\prime}(x)\) に変換します。そのために は 双方の \(x\) を \(\arcsin(x)\) に変換します。
\[\begin{eqnarray}
\arcsin^{\prime}(\sin(x))
&=&
\dfrac{1}{\cos(x)}\\
\rightarrow
\arcsin^{\prime}(\sin(\arcsin(x)))
&=&
\dfrac{1}{\cos(\arcsin(x))}\\
\rightarrow{}
\arcsin^{\prime}(x)
&=&
\dfrac{1}{\sqrt{1-x^2}}
\end{eqnarray}\]
なお、『arcsin（アークサイン）の微分を誰でもわかるように解説』でも詳しく解説しているので、ぜひ合わせてご確認ください。
それでは見ていきましょう。
2.2. arccos (cos^-1) の微分
arcsin と sin の関係と同じように arccos は cos の逆関数です。そのため、\(y=\cos(x)\)、\(x=\arccos(y)\) となります。そのため、arccos の微分は逆関数の微分公式を使って cos から求めることができます。
以下の通りです。
arccos の微分の証明（逆関数の微分公式より）
\[\begin{eqnarray}
\arccos^{\prime}(y)
&=&
\dfrac{1}{\cos^{\prime}(x)}\\
&=&
\dfrac{1}{-\sin(x)}\\
\end{eqnarray}\]
これは \(\arccos^{\prime}(y)=\arccos^{\prime}(\cos(x))\) なので \(\arccos^{\prime}(x)\) に変換します。そのために両辺の \(x\) を \(\arccos(x)\) に変換します。
\[\begin{eqnarray}
\arccos^{\prime}(\cos(x))
&=&
\dfrac{1}{-\sin(x)}\\
\rightarrow
\arccos^{\prime}(\cos(\arccos(x)))
&=&
\dfrac{1}{-\sin(\arccos(x))}\\
\rightarrow{}
\arccos^{\prime}(x)
&=&
-\dfrac{1}{\sqrt{1-x^2}}
\end{eqnarray}\]
『arctan（アークタンジェント）の微分を誰でも理解できるように解説』でも詳しく解説しているので、ぜひ合わせてご確認ください。
2.3. arctan (tan^-1) の微分
同じく arctan は tan の逆関数です。そのため、\(y=\tan(x)\)、\(x=\arctan(y)\) となります。そして、arctan の微分は逆関数の微分公式を使って tan から求めることができます。
以下の通りです。
arctan の微分の証明（逆関数の微分公式より）
\[\begin{eqnarray}
\arctan^{\prime}(y)
&=&
\dfrac{1}{\tan^{\prime}(x)}\\
&=&
\dfrac{1}{\frac{1}{\cos^2(x)}}\\
&=&
\cos^2(x)
\end{eqnarray}\]
これは \(\arctan^{\prime}(y)\) なので \(\arctan^{\prime}(x)\) に変換します。そのために両辺の \(x\) を \(\arctan(x)\) に変換します。
\[\begin{eqnarray}
\arctan^{\prime}(\tan(x))
&=&
\cos^2(x)\\
\rightarrow
\arctan^{\prime}(\tan(\arctan(x)))
&=&
\cos^2(\arctan(x))\\
\rightarrow{}
\arctan^{\prime}(x)
&=&
\dfrac{1}{(\sqrt{1+x^2})^2}\\
&=&
\dfrac{1}{1+x^2}
\end{eqnarray}\]
『arccos（アークコサイン）の微分を誰でも理解できるように解説』でも詳しく解説しているので、ぜひ合わせてご確認ください。
3. 逆三角関数の微分まとめ
以上が逆三角関数の微分です。
全く難しいものではありませんが、文中でお伝えしている通り、これを理解するためには、三角関数と逆関数、そしてその微分をしっかりと理解していることが必要です。もし解説の中でわからないところがあったとしたら、それぞれの解説ページもぜひ確認してみてください。そうすれば、必ずわかるようになります。
参考になったなら嬉しく思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント