当ページでは逆関数の微分公式と、その証明を誰でもわかるように視覚的に解説しています。具体的には、以下のことがわかります。
- 逆関数とは何か・書き方・求め方
- 逆関数の微分公式
- 逆関数の微分公式の証明
ぜひ、参考にして頂ければと思います。
1. 逆関数
まず逆関数について簡単におさらいしておきましょう。ここでは、次の3点について振り返ります。
- 逆関数とは何か
- 逆関数の表記方法
- 逆関数の求め方
さっそく見ていきましょう。
1.1. 逆関数とは
逆関数とは、簡単に言うと「ある関数から出てきた出力値を受け取って、元々の入力値を返す関数」のことです。言い換えると「出力値を入力値に戻す関数」、もっと簡単に言うと「元に戻す関数」です。
例えば関数 \(f(x)=x^3\) の出力値を、その逆関数 \(g(y)=\sqrt[3]{y}\) に入力すると、以下のように元々の入力値である \(x\) が出力されます。
関数と逆関数の関係
\[
g(f(x))=x
\]
\[\begin{eqnarray}
2
\xrightarrow{入力}
\fbox{$x^3$}
\xrightarrow{出力}
&8&
\xrightarrow{入力}
\fbox{$\sqrt[3]{x}$}
\xrightarrow{出力}
2\\
3
\xrightarrow{入力}
\fbox{$x^3$}
\xrightarrow{出力}
&27&
\xrightarrow{入力}
\fbox{$\sqrt[3]{x}$}
\xrightarrow{出力}
3\\
&\vdots&\\
x
\xrightarrow{入力}
\fbox{$x^3$}
\xrightarrow{出力}
&x^3&
\xrightarrow{入力}
\fbox{$\sqrt[3]{x}$}
\xrightarrow{出力}
x\\
\end{eqnarray}\]
これが関数と逆関数の関係です。
そして重要な点として、関数と逆関数は、視覚的には \(y=x\) を挟んで対称という関係になっています。
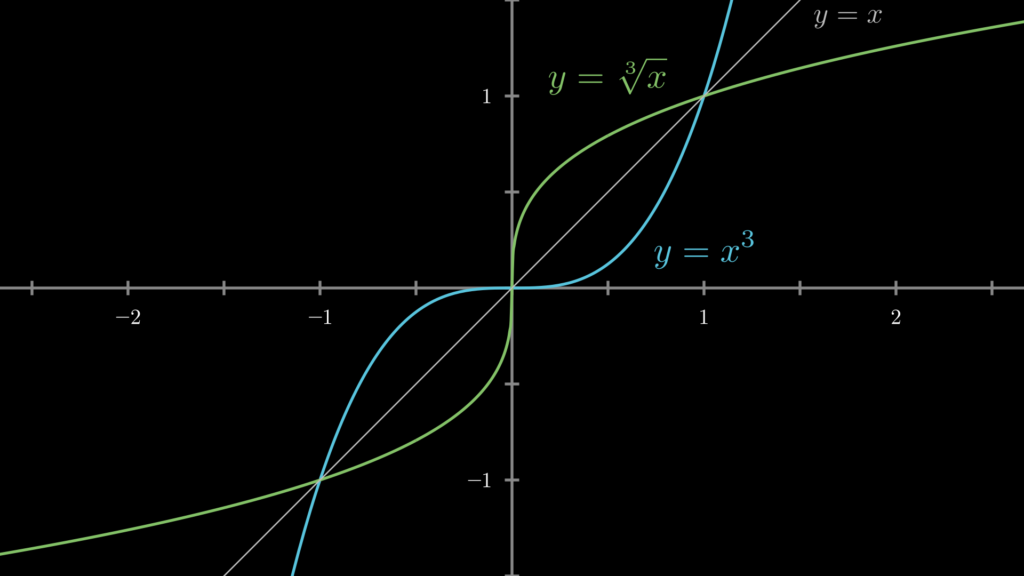
以上が逆関数です。
1.2. 逆関数の表記
あらためて逆関数の表記方法を確認しておきましょう。
関数 \(y=f(x)\) があるとき、その逆関数は \(y\) を \(x\) に戻すものなので、\(x=g(y)\) と表します。そして、これが \(f(x)\) の逆関数であることを強調したい場合は \(f^{-1}(x)\) と表します。
逆関数の表記
\[
g(y) \ \ \ or \ \ \ f^{-1}(x)
\]
とても紛らわしいのですが、この \(^{-1}\) は、べき乗を表しているのではなく、逆関数であることを表しています。
特に混乱しがちなのが、三角関数の逆関数です。例えば、\(\sin^{-1}(x)\) は、べき乗の \(\frac{1}{\sin(x)}\) ではなく、逆三角関数の \(\arcsin(x)\) を表しています。逆三角関数を扱う際は、この点に惑わされないように注意しましょう。
1.3. 逆関数の求め方
上でお伝えした通り、関数 \(y=f(x)\) の逆関数は \(x=g(y)\) になります。まさにこの関係性から、逆関数を求めることができます。
例として \(y=x^3\) の逆関数を求めてみましょう。
逆関数は、この出力値の \(y\) を入力値の \(x\) に戻すものなので、以下の通りになります。
逆関数の求め方①
\[\begin{eqnarray}
y=x^3 \ &\longrightarrow& \ x^3=y\\
&\longrightarrow& \ x=\sqrt[3]{y}
\end{eqnarray}\]
このままでも良いのですが、通常は以下のように \(y\) と \(x\) を入れ替えて、\(x\) の関数の形にします。
逆関数の求め方② \(x\) と \(y\) を入れ替える
\[x=\sqrt[3]{y} \ \longrightarrow \ y=\sqrt[3]{x}\]
以上が逆関数の求め方です。
2. 逆関数の微分公式
それでは、ここから逆関数の微分公式を見ていきましょう。
本来は、逆関数そのものが分かっていれば、その微分は、普通の微分公式で求めることができます。例えば、\(f^{-1}(x)=\sqrt[3]{x}\) の微分は、べき乗の微分公式を使って次のように求められます。
\[\begin{eqnarray}
(\sqrt[3]{x})^{\prime}&=&
(x^{\frac{1}{3}})^{\prime}&=&
\dfrac{1}{3}x^{-\frac{2}{3}}&=&
\dfrac{1}{3 \sqrt[3]{x}^2}
\end{eqnarray}\]
しかし、ときには、逆関数を微分するよりも、元の関数から逆関数の微分を求める方が楽な場合があります。そのようなときに使うのが、以下の逆関数の微分公式です。
逆関数の微分公式
\[\begin{eqnarray}
g^{\prime}(y)
&=&
\dfrac{dg}{dy}\\
&=&
\dfrac{1}{f^{\prime}(x)}\\
&=&
\dfrac{1}{\frac{dx}{dy}}
\end{eqnarray}\]
なお、この微分公式で求められるのは、逆関数を \(y\) について微分したもの \(\frac{dg}{dy}\) です。そのため通常は、これで得られる解を、\(x\) について微分したものに変換します。
例えば、\(x^3\) の逆関数の微分を、逆関数の微分公式で解くと次のようになります。
公式から \(y=x^3\) の逆関数の微分を求める①
\[\begin{eqnarray}
g^{\prime}(y)
&=&
\dfrac{dg}{dy}
&=&
\dfrac{1}{\frac{dy}{dx}}
&=&
\dfrac{1}{3x^2}
\end{eqnarray}\]
ここで \(y=x^3\) であることから、\(g(y)\) は以下のように \(g(x^3)\) であることを表します。
\[\begin{eqnarray}
g^{\prime}(y)
&=&
g^{\prime}(x^3)
=
\dfrac{1}{3x^2}
\end{eqnarray}\]
そのため、これを \(g(x)\) の形に戻すために、両辺の \(x\) を立方根します。
\[\begin{eqnarray}
g^{\prime}(\sqrt[3]{x^3})
&=&
\dfrac{1}{3\sqrt[3]{x}^2}\\
\rightarrow
g^{\prime}(x)
&=&
\dfrac{1}{3\sqrt[3]{x}^2}
\end{eqnarray}\]
以上。
このように、最後に \(g^{\prime}(y)\) を \(g^{\prime}(x)\) のかたちに変換することを忘れないようにしましょう。
もう一つ \(y=e^x\) の逆関数の微分を求めてみましょう。以下の通りです。
公式から \(y=e^x\) の逆関数の微分を求める
\[\begin{eqnarray}
g^{\prime}(y)
&=&
\dfrac{1}{(e^x)^{\prime}}\\
&=&
\dfrac{1}{e^x}\\
\end{eqnarray}\]
\(y=e^x\) から \(x=\log_{e}y\) なので、\(x\) を \(\log_{e}x\) に変換することで、\(g^{\prime}(y)\) を \(g^{\prime}(x)\) の形に変換できる。
\[\begin{eqnarray}
g^{\prime}(x)
&=&
\dfrac{1}{e^{\log_e{x}}}\\
&=&
\dfrac{1}{x}
\end{eqnarray}\]
以上。
なお指数関数と対数関数の微分については、それぞれ以下のページで解説しています。
さて、それでは、なぜこの公式で逆関数の微分を求められるのでしょうか。次にこの点について考えてみましょう。
3. 逆関数の微分公式の証明
逆関数の微分公式を理解するには、まず、逆関数の性質を思い出す必要があります。
その性質とは、関数 \(y=f(x)\) と逆関数 \(x=g(y)\) があるとき、関数 \(f(x)\) の座標が \((x,y)\) だとしたら、逆関数 \(g(y)\) の座標は \((y,x)\) になるというものです。
下図で確認しましょう。
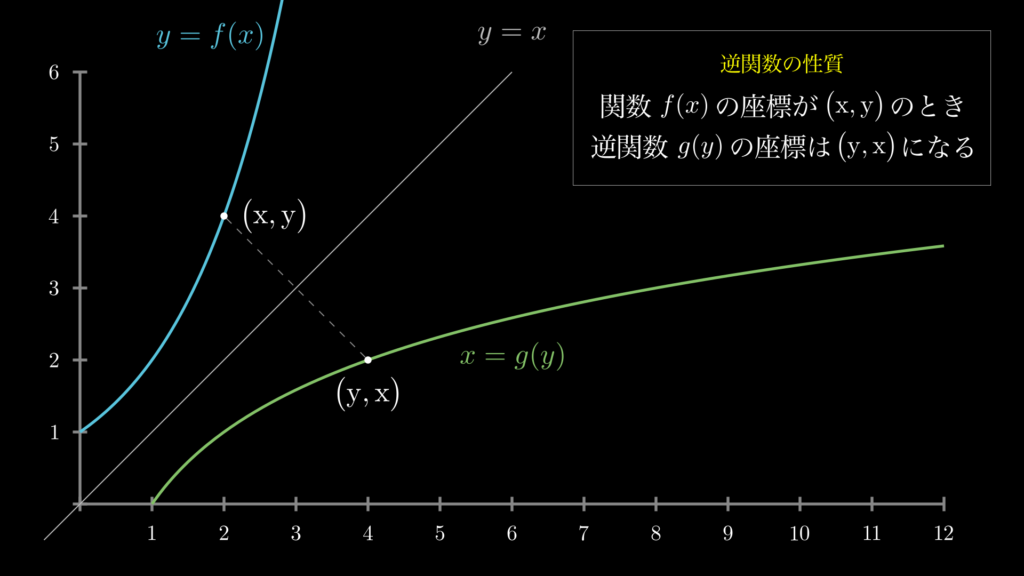
このことから、元の関数 \(y=f(x)\) において、\(x\) の値が \(dx\) 変化すると逆関数の高さが \(dx\) 変化し、それによって \(y\) の値が \(dy\) 変化すると逆関数の長さが \(dy\) 変化することがわかります。以上のことから逆関数の微分 \(g^{\prime}(y)\) は、\(\frac{dx}{dy}\) で計算できることになります。
このことは下図を見ていただくとわかりやすいでしょう。
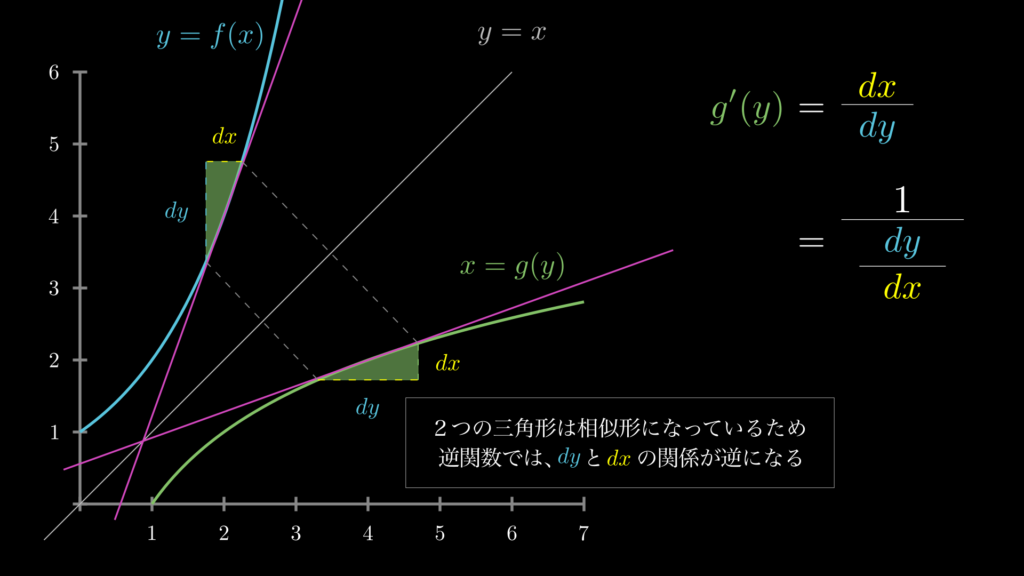
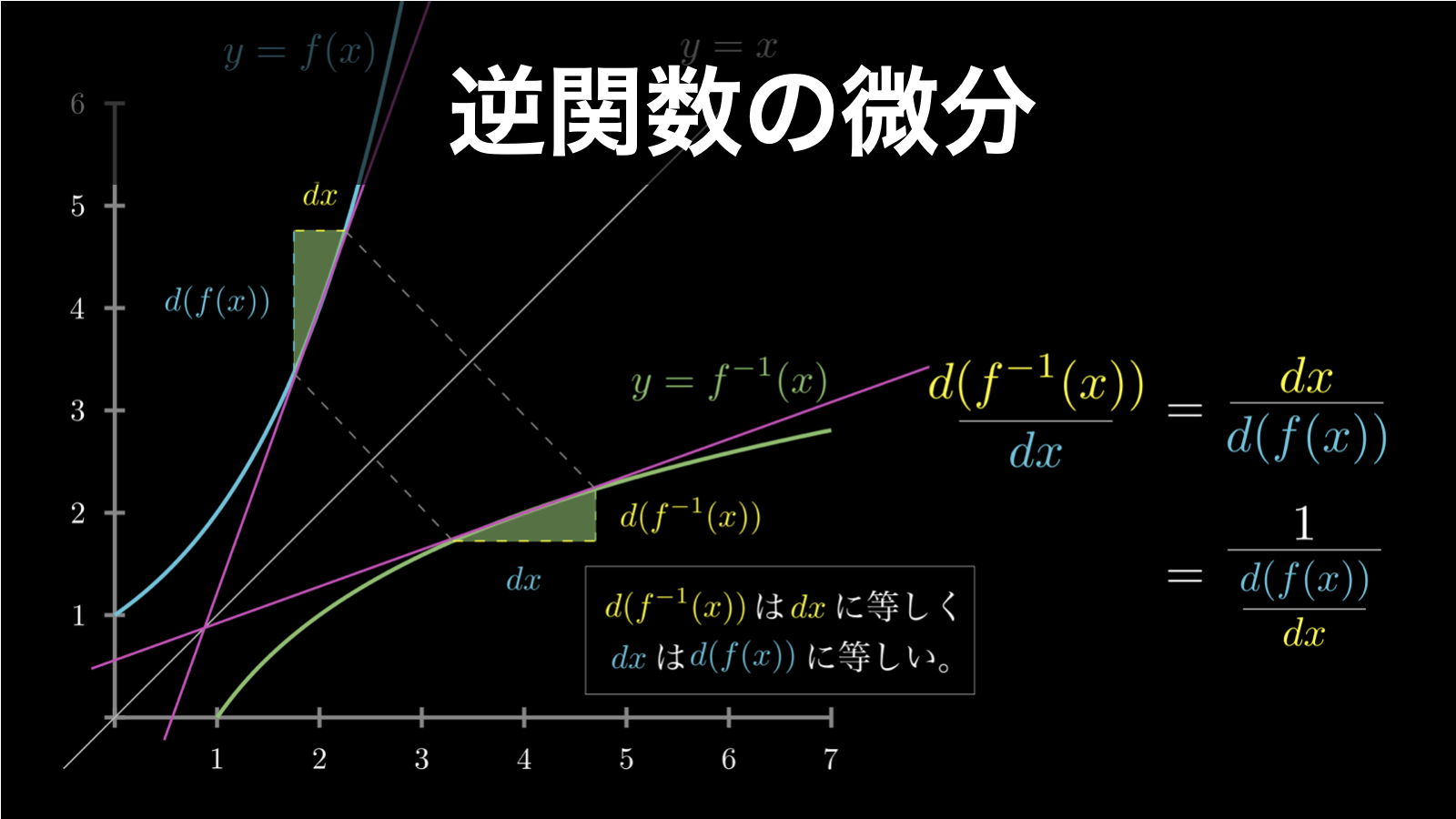
これを、元の関数 \(f(x)\) の視点からわかりやすく並べ替えたものが、上でお見せした逆関数の微分公式です。以上が、逆関数の微分公式の証明です。
なお、より一般的には、以下のように、逆関数を合成関数として解釈して、数式で証明している場合が多いですが、上のように視覚的に理解しておく方が、応用力や発想力という点でおすすめです。
合成関数の微分公式を使った証明
まず、\(y=f(x)\) の逆関数を \(x=g(y)\) とします。逆関数の性質から、これは、\(x=g(f(x))\) という合成関数の形で表すことができます。そして、合成関数の微分公式に従って、逆関数を \(x\) について微分します。すると、以下のようになります。
\[\begin{eqnarray}
x^{\prime}&=&(g^{\prime}(y))\\
\end{eqnarray}\]
\[\begin{eqnarray}
\rightarrow
x^{\prime}
&=&
\overbrace{\frac{dg}{dy}}^{外関数}
\cdot
\overbrace{\frac{dy}{dx}}^{内関数}
\end{eqnarray}\]
\(x^{\prime}=1\) なので、この式は次のように書き換えることが可能です。
\[\begin{eqnarray}
&1&=\frac{dg}{dy} \cdot \frac{dy}{dx}\\
&\rightarrow& \frac{dg}{dy} = \frac{1}{\frac{dy}{dx}}
\end{eqnarray}\]
以上。
4. 逆関数の微分まとめ
以上が逆関数の微分公式です。
とても簡単な公式ですが、盲目的に使うのではなく、なぜそうなるのかまで理解して使うようにしましょう。
理解するためのポイントは、関数と逆関数の関係をしっかりと理解することにあります。それがわかれば、逆関数の微分は、元の関数の微分の \(dy\) と \(dx\) を入れ替えたものに過ぎないことがわかります。そこから、分子分母を逆にしたら微分が求められるということになるのですね。
このことがわかるように、ぜひ当ページの解説を役立てて頂ければと思います。




コメント