分数の微分は公式を使って、簡単に解くことができます。このページでは、まず、この公式を紹介し、その後でなぜ、それらの公式で分数の微分を求めることができるのかを、誰でも理解できるように解説していきます。
特に以下のような点を深く理解することができます。
- 分数の関数とはどのようなものかがわかる
- 分数関数の公式を正確に理解できるようになる
- さまざまな微分公式の応用を肌で実感することができる
3つ目の点について補足しておくと、分数の微分公式は、以下の3つの微分公式を応用したものになっています。
そのため、分数の微分公式について考えることで、これら3つの公式の理解をさらに一歩深めることにも繋がるのですね。こうしたことを学ぶと、数学的な発想力がどんどん向上していきます。分数の微分の学習は、そうした面からもとても有益です。
それでは前置きはこれぐらいにして早速見ていきましょう。
1. 分数の関数とは
分数関数には、以下に示しているように、分母だけが関数のものと、分子も分母も関数のものの2種類があります。
分数関数
\[
\dfrac{1}{f(x)}
\hspace{7mm}
\dfrac{g(x)}{f(x)}
\]
参考までに \(f(x)=\sin(x)\), \(g(x)=x^2\) としたときのグラフを描いておきます。
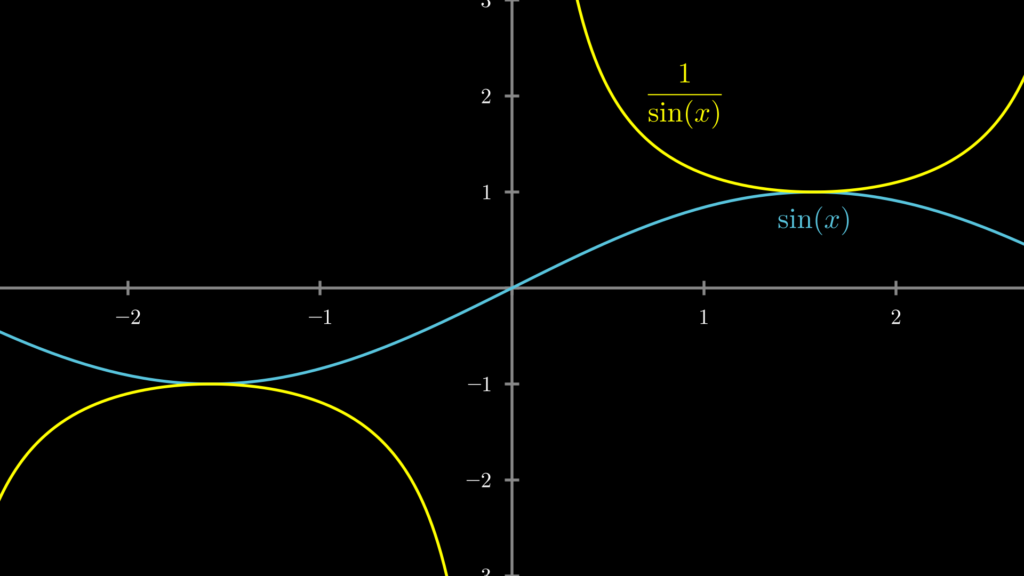
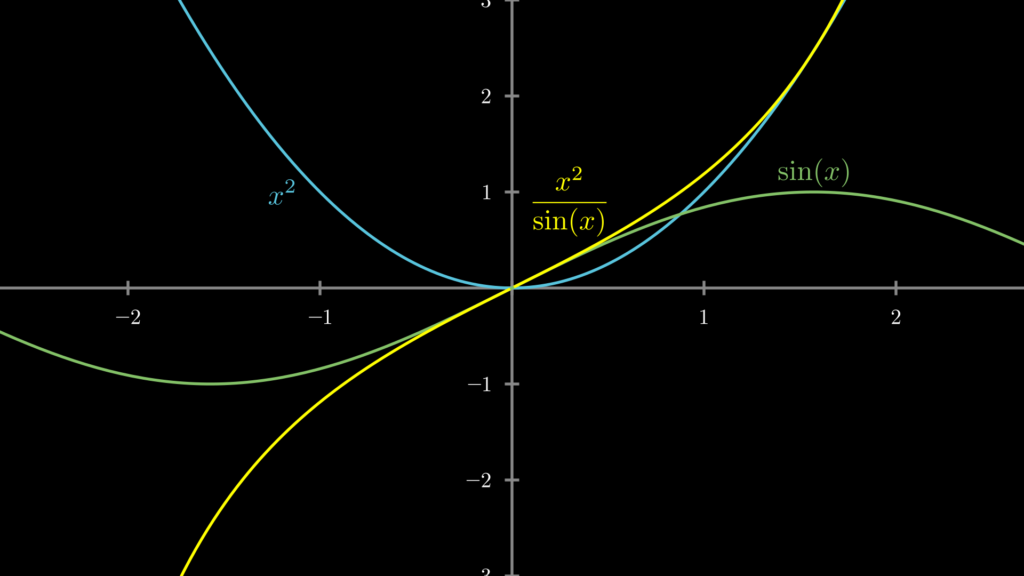
さて、それではこのような分数関数の微分はどのようにして求めるのでしょうか?次から見ていきましょう。
2. 分数の微分のやり方
結論から言うと、分数の微分はどちらも公式を使って求めることができます。それぞれ見ていきましょう。
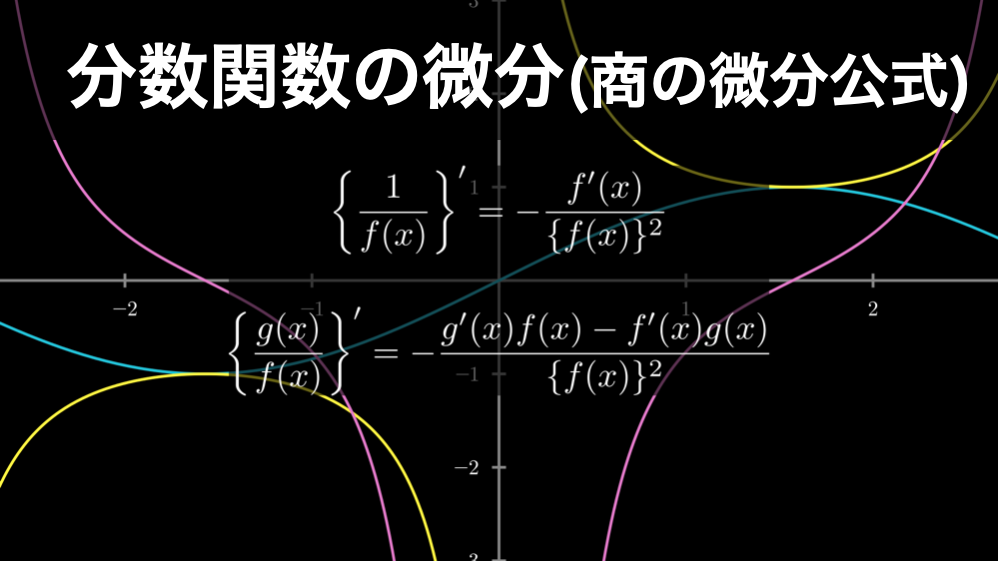
分数の微分公式
まず、分母が関数である場合の微分は以下の公式で求められます。当ページでは、これを「分数の微分公式」と呼ぶことにします。
分数の微分公式
\[
\left\{
\frac{1}{f(x)}
\right\}
{}^{\prime}
=
-\frac{f^{\prime}(x)}{\{f(x)\}^2}
\]
例えば、 \(f(x)=\sin(x)\) としたら次のようになります。
\[\begin{eqnarray}
\left\{
\frac{1}{\sin(x)}
\right\}
{}^{\prime}
&=&
-\dfrac{sin(x)^{\prime}}{\{ \sin(x)\}^2}\\
&=&
-\dfrac{\cos(x)}{\sin^2(x)}
\end{eqnarray}\]
参考までにグラフを描いておきます。
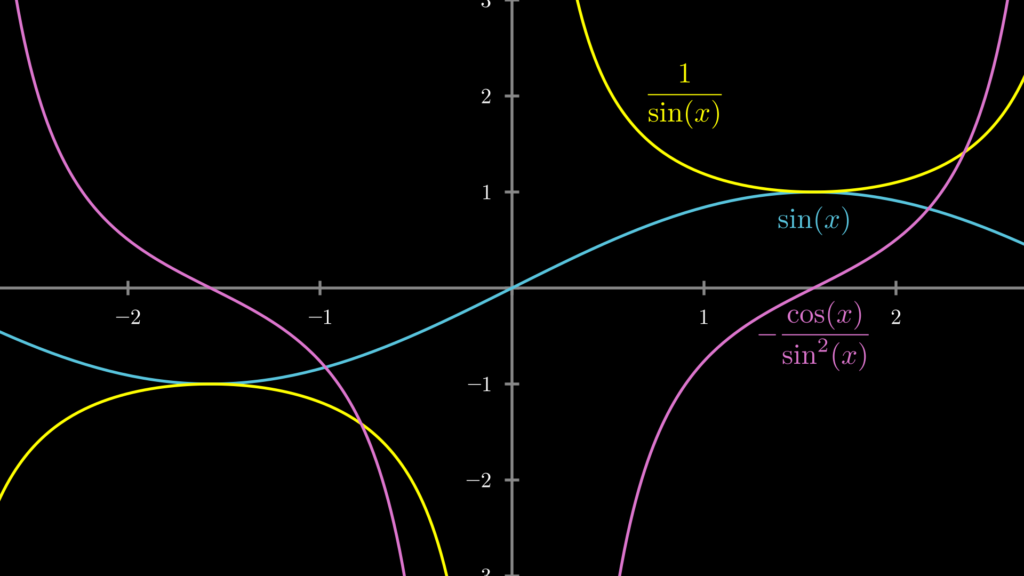
なお、三角関数の微分については『三角関数の微分が誰でも驚くほどよく分かるようになる解説』で解説していますので、復習したい場合はぜひご覧ください。
商の微分公式
分子も分母も関数である場合の微分は以下の公式で求められます。こちらは、広く「商の微分公式」と呼ばれています。
商の微分公式
\[
\left\{
\dfrac{g(x)}{f(x)}
\right\}
{}^{\prime}
=
\dfrac{g^{\prime}(x)f(x)-f^{\prime}(x)g(x)}{\{f(x)\}^2}
\]
例えば、 \(f(x)=\sin(x),\hspace{5mm} g(x)=x^2\) としたら次のようになります。
\[\begin{eqnarray}
\left\{
\dfrac{x^2}{\sin(x)}
\right\}
{}^{\prime}
&=&
\dfrac{
(x^2)^{\prime} \sin(x)- \{\sin(x)\}^{\prime}x^2
}
{ \{ \sin(x) \}^2 }
\\
&=&
\dfrac{2x\sin(x)-\cos(x)x^2}{\sin^2(x)}
\end{eqnarray}\]
これも参考にグラフを載せておきます。
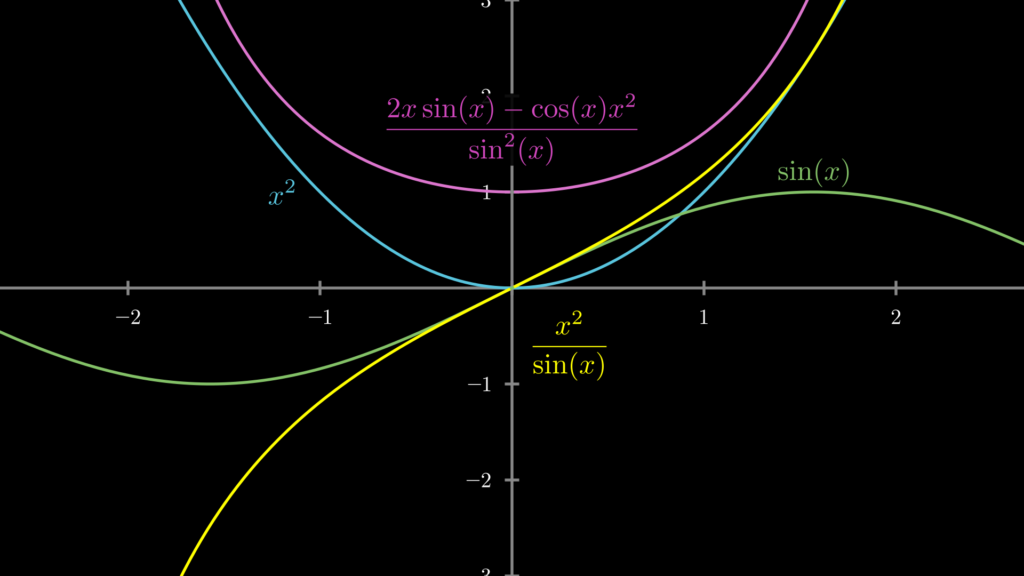
それでは、なぜ分数の微分はこれらの公式の通りになるのでしょうか?この点について深く理解することで、単に公式を盲目的に使っているだけの場合よりも、はるかに数学的な応用力や発想力が向上します。そこで、早速この点について考えていきましょう。
2. 分数の微分の解説
まずは分数の微分公式から見ていきたいと思います。
この公式について理解するコツは、分母が関数の分数を、以下の通り、-1 を指数とするべき乗に置き換えることにあります。なお、べき乗関数の微分については『べき乗(累乗)の微分公式-誰でも必ず深く理解できるように解説-』で解説しています。
分数=-1 のべき乗
\[
\frac{1}{2}=2^{-1},
\hspace{7mm}
\frac{1}{3}=3^{-1},
\hspace{7mm}
\frac{1}{f(x)}=\{f(x)\}^{-1}
\]
このようにすると、分母が関数の分数は、分母の関数 \(f(x)\) と \(x^{-1}\) の2つの関数の合成関数と同じであることがわかります。
例として、 \(f(x)=\sin(x), \hspace{3mm} g(x)=x^{-1}\) としたら、次の通りです。
分母が関数の分数とは、g(x)=x-1との合成関数
\[\begin{eqnarray}
f(x)&=&\sin(x)\\
g(x)&=&x^{-1}\\
g(f(x))
&=&
\{\sin(x)\}^{-1}
\end{eqnarray}\]
そのため、分母が関数の分数は合成関数の微分公式で求めることができます。実際に求めてみましょう。なお、合成関数の微分公式は『合成関数の微分を誰でも直観的かつ深く理解できるように解説』で詳しく解説していますので、ぜひご覧ください。
分母が関数の分数の微分は、合成関数の微分公式で求める
\[\begin{eqnarray}
\left( \frac{1}{f(x)} \right)^{\prime}
&=&
\left(\{f(x)\}^{-1}\right)^{\prime}\\
&=&
-f(x)^{-2}\cdot f(x)^{\prime}\\
&=&
-\dfrac{1}{f(x)^2}\cdot f(x)^{\prime}\\
&=&
-\frac{f(x)^{\prime}}{f(x)^2}
\end{eqnarray}\]
分数の公式の通りになりましたね。
このように分数関数の微分は、べき乗微分公式と合成関数の微分公式の組み合わせで求めることができます。そして、これが求められていると、商の微分公式も簡単に導き出すことができます。
3. 商の微分公式の解説
それでは、商の微分公式について見ていきましょう。結局のところ、分子も分母も関数の分数は、以下に示している通り、2つの関数の積に過ぎません。
分子も分母も関数の微分=2つの関数の積
\[\begin{eqnarray}
\frac{g(x)}{f(x)}
&=&
g(x)\cdot \frac{1}{f(x)}\\
&=&
g(x)\cdot \{f(x)\}^{-1}
\end{eqnarray}
\]
そのため、これは積の微分公式で解くことができます。
積の微分公式
\[\begin{eqnarray}
\{g(x)f(x)\}^{\prime}
&=&
g^{\prime}(x)f(x)+g(x)f^{\prime}(x)
\end{eqnarray}
\]
それでは実際に解いてみましょう。
分子も分母も関数である分数の微分は積の微分法則で求める
\[\begin{eqnarray}
\left\{ \frac{g(x)}{f(x)} \right\}^{\prime}
&=&
\left\{
\left( g(x) \frac{1}{f(x)} \right)
\right\}^{\prime}\\
&=&
g^{\prime}(x) \left( \dfrac{1}{f(x)} \right)
+
g(x) \left( \dfrac{1}{f(x)} \right)^{\prime}\\
&=&
g^{\prime}(x) \left( \dfrac{1}{f(x)} \right)
+
g(x)
\left( -\frac{f(x)^{\prime}}{\{f(x)\}^2} \right)\\
&=&
\dfrac{g^{\prime}(x)f(x)-f^{\prime}(x)g(x)}{\{f(x)\}^2}
\end{eqnarray}\]
商の微分公式が出てきましたね。
このように商の微分公式は、分数の微分公式と積の微分公式の組み合わせで導き出されます。
4. 分数の微分まとめ
以上が分数の微分です。
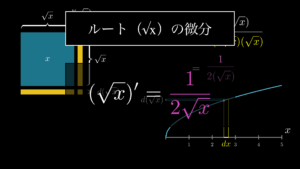
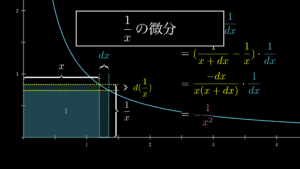
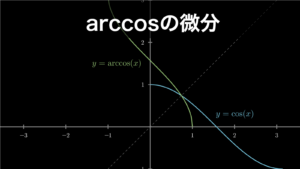
ここまで解説してきたように、分数の微分は公式を暗記していれば簡単に解くことができます。しかし、これはべき乗の微分公式・合成関数の微分公式・積の微分公式の3つの基本公式の応用に過ぎません。そのため、基本公式は必ず深く理解するようにしておきましょう。
本文中でも既にお伝えしていますが、以下のページではこの基本公式を深く理解できるようになっていますので、ぜひご覧になってみてください。




コメント