cos(x)を微分すると-sin(x)になります。
なぜこうなるのでしょうか？その理由がわかると、単に公式を暗記するだけの場合と比べて、遥かに微分を深く理解できるようになります。そこで当ページでは、cosの微分について、誰でも理解できるようにアニメーションを使いながら、詳しく解説していきます。
それではさっそく見ていきましょう。
なおsinの微分については、『sinの微分はなぜcos？誰でも直観的に理解できるように解説』で解説しているので、ぜひ併せてご確認ください。
1. cos とは
最初にcosについて簡単に復習しておきましょう。
cosは、単位円（半径が１の円）上にできる、角度をθ・斜辺の長さを１とする直角三角形の隣辺の長さのことです。そして、斜辺の長さが１ではないとしても、それが直角三角形であれば、sin の値は必ず「隣辺／斜辺」に等しくなります。
cos(θ)の長さは θが 0 と π（180度）のときに最長の 1 または -1 になり、1/2π（90度）のときと、 3/2π（270度）のときは 0 になります。
以下のアニメーションを確認すると思い出しやすいでしょう。
この cos(θ)の長さを、横軸がθ・縦軸がcos（θ）のグラフに描いたものが有名なコサインカーブ（余弦波）です。
以上がcosです。
2. cosの微分は−sin
冒頭でもお伝えした通り、cosの微分は-sinになります。以下のアニメーションで、このことを視覚的に確認することができます。
cosの微分公式
\[
\cos^{\prime}(\theta)
=
-\sin(\theta)
\]
3. cosの微分の証明
さて、それではなぜ、cosの微分は-sinになるのでしょうか。
これの証明はsinの微分の証明とほとんど同じです。cosの微分は、θの値のわずかな変化 dθと、それによる cosθの値の変化 d(cos(θ)) との割り算で計算します。この計算が、どのようなものであるのかを視覚的に確認していくことでcosの微分が必ず-sinになることが明らかになるのです。
sinの微分の計算方法
\[
\cos^{\prime}(\theta)
=
\dfrac{df(x)}{dx}
=
\dfrac{d(\cos(\theta))}{d\theta}
\]
それでは、dθと d(cos(θ)) はそれぞれ何を意味するのでしょうか。このような三角関数について考える時は、単位円上の直角三角形をイメージするのが鉄板です。
なお、単位円をイメージする際は、「ラジアン」の知識が必須になります。そこで、まずはラジアンとは何だったかを復習しておきましょう。
3.1. ラジアンの復習
ラジアンとは、単位円上の直角三角形の「なす角（θ）」であると同時に、その角度の時の孤の長さでもあります。θが 1 ラジアンの時は孤の長さも 1 になりますし、θが 2 ラジアンの時は孤の長さも 2 になります。そして、2π (6.28) ラジアンが円周の長さに相当します。
角度で言えば、2πラジアン＝360° になります。
以下のアニメーションをご覧頂くと、より簡単に理解できるでしょう。
このラジアンの知識はcosに限らず、三角関数の微分を考える上でのカギとなります。もしこの説明で不十分な場合は、各自でしっかりと学び直しておきましょう。
3.2. dθと d(cos(θ)) の幾何学的意味
さて、それでは dθと d(cos(θ)) は単位円上において何を意味するでしょうか。
まずθは孤の長さなので、θが dθ増加した時は当然、孤が dθ長くなります。そしてd(cos(θ))はθが dθ変化した時の cos(θ) の変化です。これらは視覚的に確認すると、とてもよく分かるようになりますので、ぜひ以下のアニメーションをご覧ください。
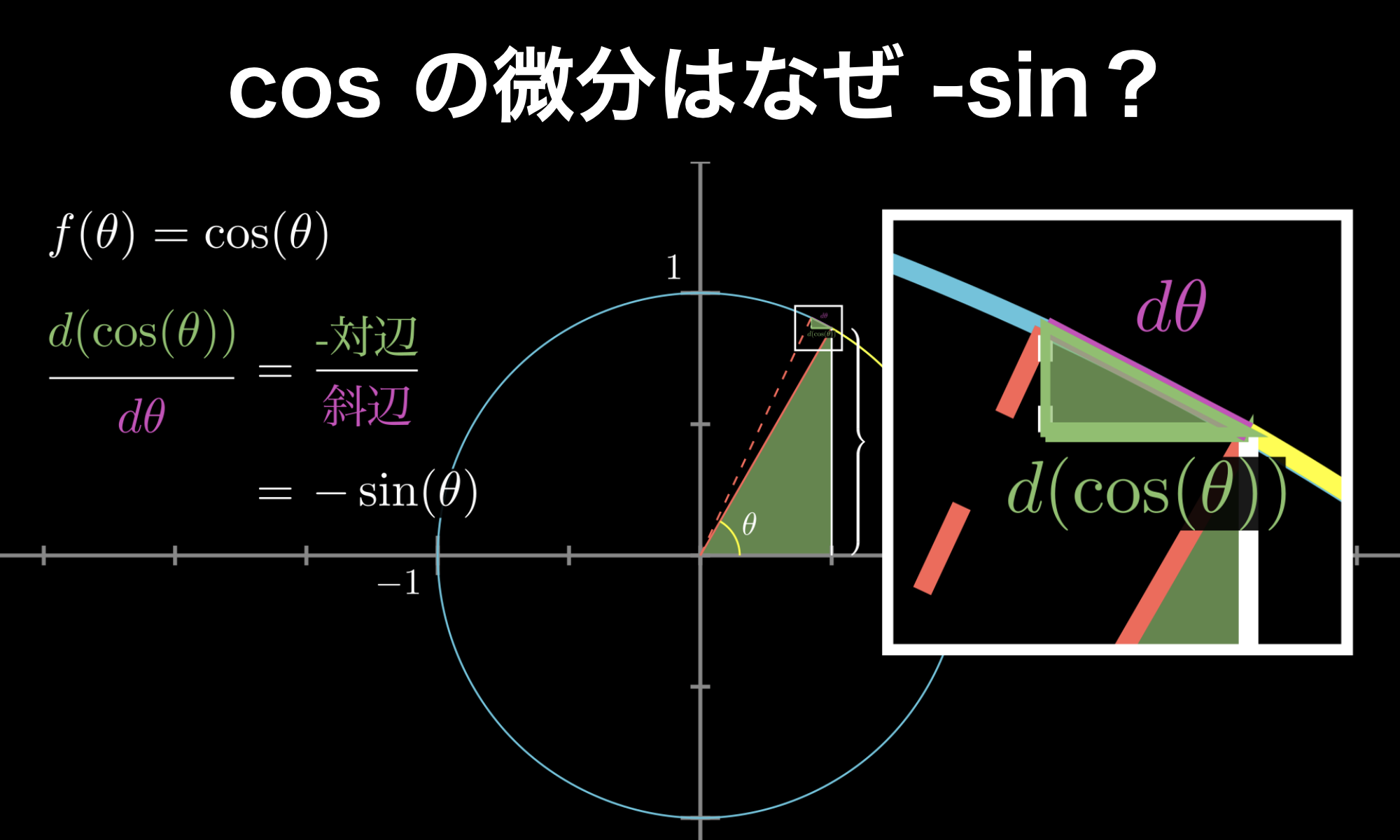
3.3. cosの微分は「-対辺／斜辺」と同じ
このdθとd(cos(θ))が作る小さな直角三角形に注目してみましょう。そう、これは元々の直角三角形と相似形になっているのです。このことから、「d((cos(θ))／dθ」の計算は、「-対辺／斜辺」の計算をしているものであることがわかります。
なお、対辺に負の符号がついているのは、dθが増加すれば d((cos(θ)) が減少し、dθが減少すれば d((cos(θ)) が増加するという関係にあるからです。
話を戻すと、「対辺／斜辺」はまさにsinの定義そのものです。以上のことから、cosの微分は必ず-sinとなるのです。
以下のアニメーションで、ぜひ、このことについての理解を深めてください。
\(\cos^{\prime}(\theta)=-\sin(\theta)\) の証明
\[
\sin^{\prime}(\theta)
=
\dfrac{dy}{dx}
=
\dfrac{d(\cos(\theta))}{d\theta}
=
\dfrac{−対辺}{斜辺}
=
-\sin(\theta)
\]
4. cosの微分のまとめ
以上がcosの微分の解説です。
単に公式を暗記して問題を解くだけの場合よりも、こうやって、「なぜ？」を考えていくことには、とても大きな価値があります。少しでも参考になったなら嬉しく思います。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント