1/xの微分を誰でも簡単に深く理解できるように解説

2021 4/29

2021年4月28日 2021年4月29日

ここでは、1/x の微分のやり方について、誰でもすぐにわかるように解説していきます。これは、いくつかのことを思い出せば、驚くほど簡単に理解できるようになります。

前置きはこれだけにして、早速、見ていきましょう。

1. 1/xの微分の求め方

結論からお伝えすると、1/x の微分はべき乗の微分公式で簡単に解くことができます。

べき乗の微分公式

\[
(x^n)^{\prime}=nx^{n-1}
\]

なぜなら分数は、以下に示している通り、負の数をべき指数とするべき乗・・・だからです。また \(x^n \cdot x^{-n}=1\) であるという点も重要です。

分数は負の数のべき乗

\[\begin{eqnarray}
\dfrac{1}{x}=x^{-1} &\longrightarrow& x \cdot x^{-1}=1\\
\dfrac{1}{x^2}=x^{-2} &\longrightarrow& x^2 \cdot x^{-2}=1\\
&\vdots&\\
\dfrac{1}{x^n}=x^{-n} &\longrightarrow& x^n \cdot x^{-n}=1
\end{eqnarray}\]

このように 1/x をべき乗に変換すれば、その微分は、以下のように、べき乗の微分公式で簡単に求めることができます。

1/x の微分

\[\begin{eqnarray}
(\dfrac{1}{x})^{\prime}&=&(x^{-1})^{\prime}\\
&=&
-1x^{-2}\\
&=&
-\dfrac{1}{x^2}
\end{eqnarray}\]

さて、単純に微分の問題を解くだけなら、ここまでを押さえておけば十分です。しかし、微分の応用分野に進むと、微分を深く理解しているのといないのとでは、発想力や思考力という点で大きな差ができてしまいます。

そこで、1/xの微分をもっと深く考えていきましょう。

2. 1/xの微分を視覚的に解説

ここからは 1/x の微分をより深く理解できるように、これを視覚的（幾何学的）に解説していきます。

前提として、累乗（べき指数が自然数のべき乗）は、以下の画像のように四角形の面積や、立方体の体積としてイメージすると深く理解できるという点を思い出しておいて下さい。

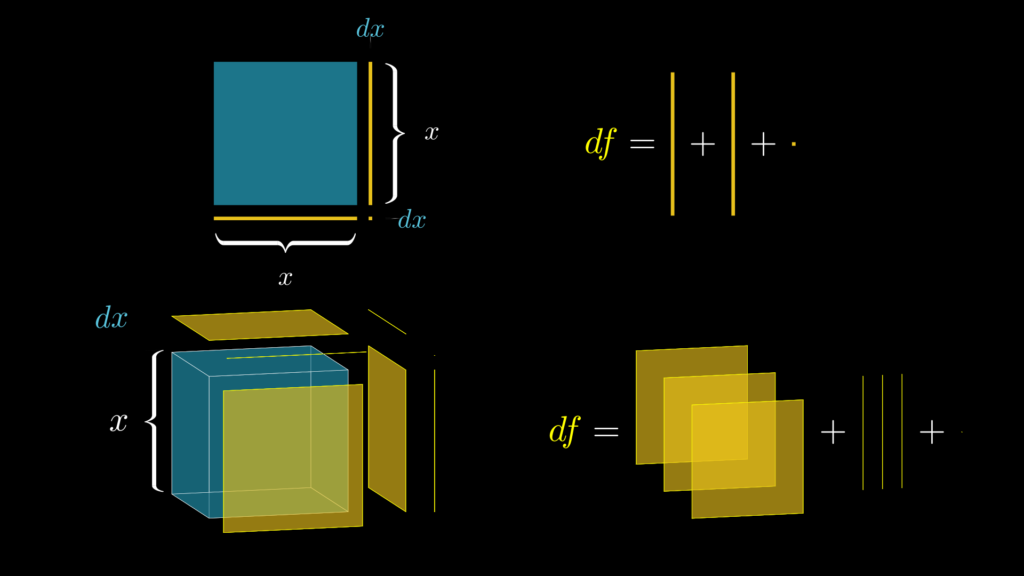
なお、これについては『べき乗（累乗）の微分公式-誰でも必ず深く理解できるように解説-』で解説していますので、まだご覧になっていない場合は、ぜひご確認ください。

それでは、べき指数が負の値のべき乗関数 \(\frac{1}{x}\) は、幾何学的にはどのようにイメージできるでしょうか？ \(x \cdot x^{-1}=1\) であることから、これは面積が常に１の四角形として考えることができます。

ぜひ以下のアニメーションでご確認ください。

べき指数が負の値のべき乗関数のイメージ

さて、『微分とは何か？誰でもわかりやすく理解できるようにイメージで解説』で解説している通り、微分とは \(x\) の値がわずかに \(dx\) だけ変化したときの瞬間の変化率のことでしたね。

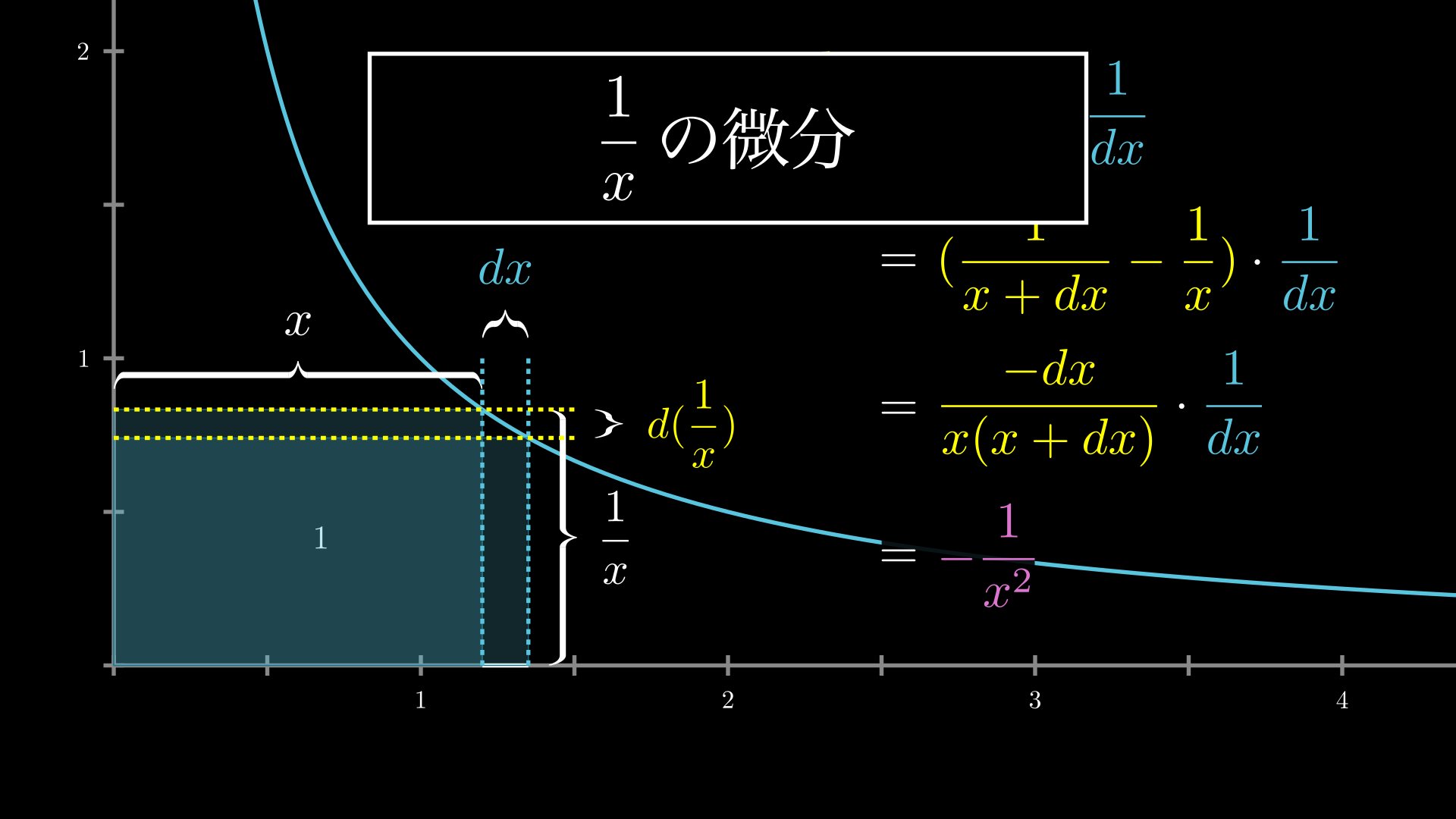
これを視覚的に考えると、面積が常に \(1\) である長方形の横の長さが \(dx\) 増加し、反対に高さが \(d(\frac{1}{x})\) 減少します。そして微分とは \(\frac{dy}{dx}\) のことなので、この高さの減少分を、横の長さの増加分で割ったものが \(\frac{1}{x}\) の微分です。

ここまでを以下のアニメーションでご確認ください。

\(x^{-1}\) の幾何学的なイメージ

これが \(x^{-1}\) の微分が意味するものです。そして、これを計算式で表したものが以下です。

1/x の微分の証明（微分の定義式より）

\[\begin{eqnarray}
\dfrac{dy}{dx}&=&\dfrac{d(\frac{1}{x})}{dx}\\
&=&
(\dfrac{1}{x+dx}-\frac{1}{x})\cdot \dfrac{1}{dx}\\
&=&
(\dfrac{x}{(x+dx)x}-\frac{x+dx}{x(x+dx)})\cdot \dfrac{1}{dx}\\
&=&
\dfrac{-dx}{x^2+xdx}\cdot \dfrac{1}{dx}\\
&=&
\dfrac{-dx}{x^2}\cdot \dfrac{1}{dx}\\
&=&
-\dfrac{1}{x^2}
\end{eqnarray}\]

これが 1/x の微分を、べき乗の微分公式で求められることの証明です。