条件付き確率とは、「事象 B が起こった条件下での事象 A の確率」のことです。このページでは、この条件付き確率についてわかりやすく解説していきます。具体的には以下の内容を知ることができます。
- 条件付き確率とは何かが具体的にわかる
- 条件付き確率の公式と使い方を例題を通して理解できる
- 後学のベイズの定理に出てくる逆確率(尤度)の触りを理解できる
- 問題を通して条件付き確率の理解を深めることができる
- 条件付き確率とベイズの定理の関係がわかる
それでは早速見ていきましょう。
1. 条件付き確率の公式
最初に公式からお伝えすると、条件付き確率は、以下の計算で求めることができます。
条件付き確率の公式
\[\begin{eqnarray}
P(A|B)
=
\dfrac{P(A \cap B)}{P(B)}
=
\dfrac{A \ {\smallと} \ B \ {\smallが同時に起こる確率}}{B \ {\smallが起こる確率}}
\end{eqnarray}\]
1.1. 条件付き確率の例
例として次のような場合を考えてみましょう。
- 事象 \(A\):糖尿病である
- 事象 \(B\):肥満である
- 積事象 \(A \cap B\):糖尿病であると同時に肥満である
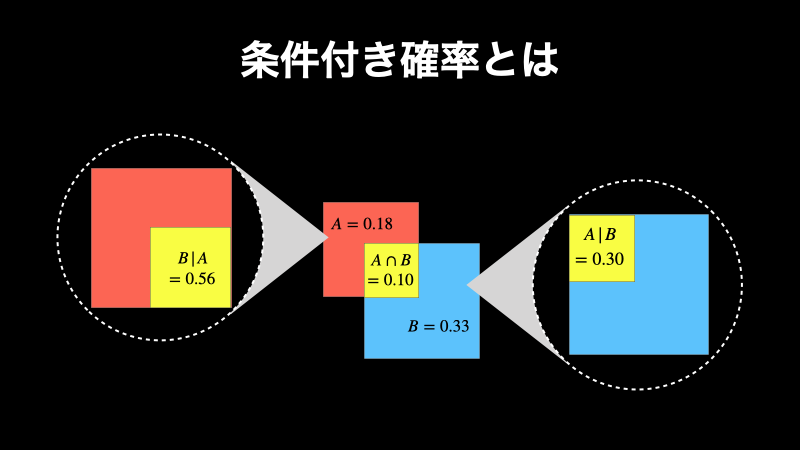
日本では \(18.0 \%\) 男性が糖尿病なので、\(P(A)=0.18\) とします。そして日本では \(33.0 \%\) の男性が肥満ですので、\(P(B)=0.33\) となります。さらに糖尿病であると同時に肥満である確率は \(P(A \cap B)=0.10\)とします。
なお重要な点として、事象 \(\small A\) と \(\small B\) はお互いに独立ではないので、確率の乗法定理で \(\small P(A \cap B)=P(A)P(B)\) とはならないという点を理解しておきましょう。条件付き確率 \(P(A|B)\) で対象となる、事象 \(A\) と事象 \(B\) は常に従属事象です。
さて、それぞれまとめると以下の通りです。
- \(P(B)=0.33\):肥満である確率
- \(P(A)=0.18\):糖尿病である確率
- \(P(A \cap B)=0.10\):肥満であり糖尿病である確率
このように、それぞれの確率がわかっている場合、肥満である人が糖尿病である条件付き確率 \(P(A|B)\) は次の通り求められます。
\[\begin{eqnarray}
P(A|B)
=
\dfrac{P(A \cap B)}{P(B)}
=
\dfrac{0.10}{0.33}
\approx
0.30
\end{eqnarray}\]
このことから、先進各国が肥満を減らそうとする政策を取るのは合理的であることがわかります。
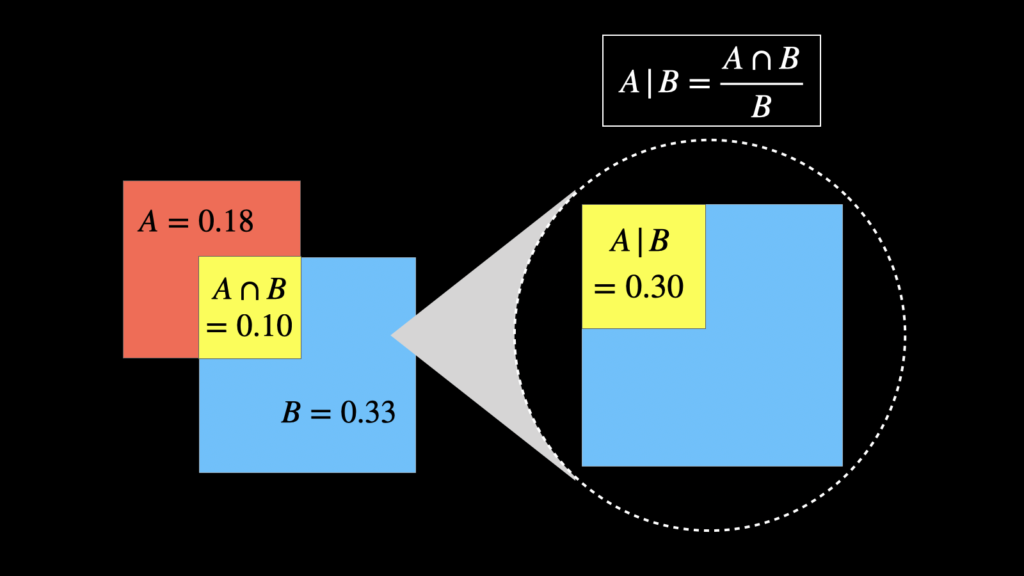
このように、事象 \(A\) と \(B\) が同時に起こる確率から、事象 \(B\) が起こる確率を割ることで、「\(B\) という条件下において \(A\) という事象が起こる確率」を求めることができます。これが条件付き確率です。なお、条件付き確率を視覚的に表すと下図のようになっています。
1.2. 条件付き確率と逆確率
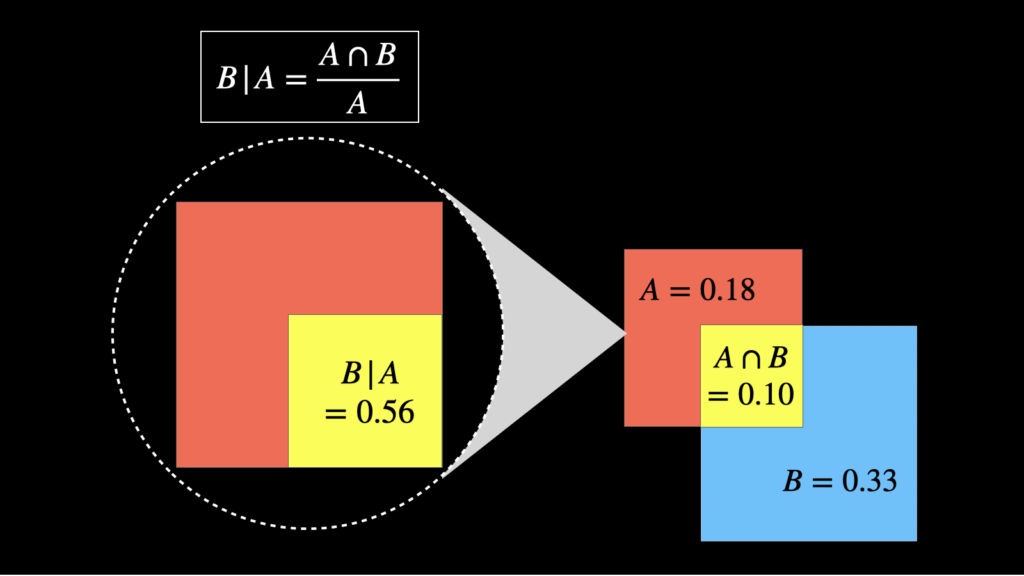
\(P(A \cap B)=P(B \cap A)\) なので(\(A\) と \(B\) が同時に起こる確率 = \(B\) と \(A\) が同時に起こる確率)、上の公式をひっくり返せば、糖尿病である人が肥満である確率 \(P(B|A)\) も以下の通り求めることができます。
\[\begin{eqnarray}
P(B|A)
=
\dfrac{P(B \cap A)}{P(A)}
=
\dfrac{0.10}{0.18}
\approx
0.56
\end{eqnarray}\]
この \(P(B|A)\) を \(P(A|B)\) に対する「逆確率」と言います。
\(P(A|B)\) は肥満(原因)であるという条件下で糖尿病(結果)である確率なので、 \(P({\small 結果}|{\small 原因})\) です。つまりこれは肥満が糖尿病の原因である確率だと解釈できます。これを因果関係と言います。
一方で \(P(B|A)\) は糖尿病(結果)という結果が見られる場合に肥満(原因)である確率なので、 \(P({\small 原因}|{\small 結果})\) です。これは糖尿病という結果がある時に肥満という原因がどれだけ見られるかということを表しています。これを「尤度」と言います。この逆確率(尤度)の概念は、後にベイズの定理を学ぶときに出てきますので、ぜひ頭に入れておいてください。
2. 条件付き確率の問題
条件付き確率をより深く理解するために、ここで、一つ応用問題を解いてみましょう。早速、次の問題をご覧ください。
条件付き確率の公式をより深く理解できる問題
ある国では、人口の 4.25% が性同一性障害(GID)を抱えているとします。そして女性では割合が 1% であり、男性では 8% です。なお人口における男女比は 50対50 であると仮定します。
この場合、それぞれの確率は次のように示すことができます。
- \(P(GID) = 0.0425 \cdots\) 性同一性障害の確率
- \(P(GID | 男性) = 0.08 \cdots \) 男性の場合で性同一性障害の確率
- \(P(GID | 女性) = 0.01 \cdots \) 女性の場合で性同一性障害の確率
さて、それではランダムに 1 人を選んで、その人が GID であり男性である確率 \(P(GID∩{\small 男性})\) は、どう求められるでしょうか。
正しい解答
GIDであるという事象を \(A\)、男性であるという事象を \(B\) とします。今回求めたいのは、条件付き確率の \(P(A|B)\) ではなく、同時確率の \(P(A \cap B)\) です。
これは条件付き確率の公式を変形して、以下の式で求められます。
\[\begin{eqnarray}
P(A|B)
=
\dfrac{P(A \cap B)}{P(B)}
\ \ \ \overset{変形}{\Longrightarrow} \ \ \
P(A \cap B)=P(B)P(A|B)
\end{eqnarray}\]
問題文より、\(P(A|B)=0.08\)、\(P(B)=0.5\) であることがわかっているので、答えは次の通りになります。
\[\begin{eqnarray}
P(A \cap B)=P(B)P(A|B)
=0.5 \times 0.08=0.04
\end{eqnarray}\]
以上が正解です。
補足 \(P(B)P(A|B)=P(A)P(B|A)\)
同時確率では、\(P(A \cap B)=P(B \cap A)\) です。そのため以下が成り立ちます。
\[P(A \cap B)=P(B \cap A)=P(B)P(A|B)=P(A)P(B|A)\]
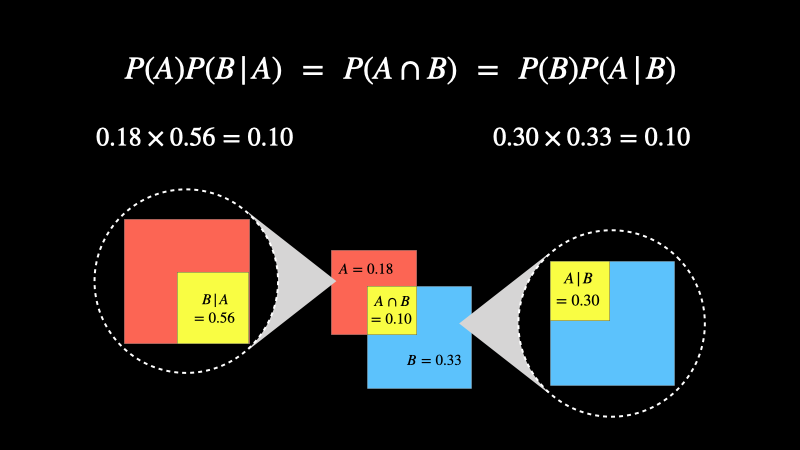
これを覚えておくと、後々すぐに役立ちますので、頭に入れておきましょう。これをイメージで表しているのが下図です。
間違った解答
なお、問題をみて瞬間的に次のように、確率の乗法定理を使って解答してしまった方も少なくないと思います。
\[\begin{eqnarray}
P(GID \cap 男性)
&=&
P(GID) \times P(男性)
&=&0.0425 \times 0.5 = 0.02125
\end{eqnarray}\]
しかし少し考えれば、これは明らかに正しくないことがわかります。
なぜならこの計算だと、女性かつ GID である確率も \(P({\small 女性} ∩ GID)\)\(=0.5\times 0.0425=0.02125\) と、同じ確率になってしまうからです。これはおかしいです。女性が GID である確率は、男性と比べてはるかに低いのですから、\(P({\small 女性} ∩ GID)\)は、\(P({\small 男性} ∩ GID)\) より低くならなければいけません。
なぜ、こうなってしまうのでしょうか。
理由は、上でも述べた通り、確率の乗法定理は、独立事象の場合にしか通用しないからです。そして、この問題では、男性である確率と GID である確率、女性である確率と GID である確率は、それぞれ独立事象ではありません。
以上のことから、確率の乗法定理を使った解答は誤りであることになります。
従属事象の同時確率と独立事象の同時確率の違い
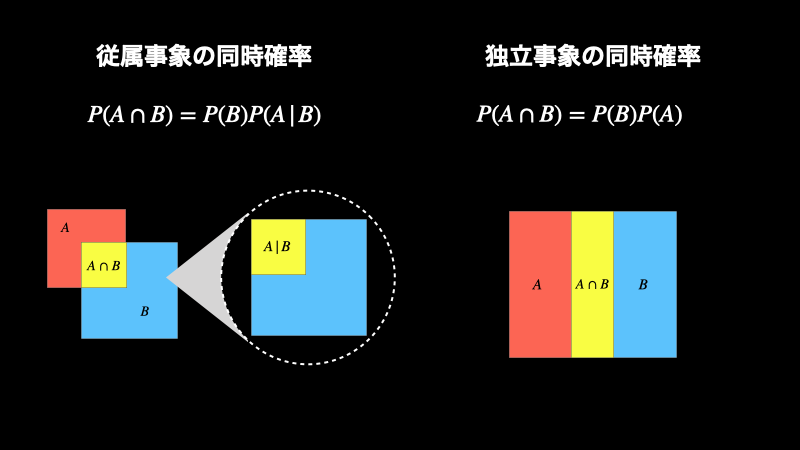
同時確率 \(P(A \cap B)\) を求める際、独立事象同士の場合は、確率の乗法定理を使う。従属事象同士の場合は、条件付き確率の公式を変形して使う。なお独立事象の同時確率と、従属事象の同時確率の違いをイメージにしたものが下図です。
3. 条件付き確率とベイズの定理
さて、ここまでで条件付き確率について解説してきました。しかし、実のところ条件付き確率を使うケースはそれほど多くありません。それでは、なぜわざわざ条件付き確率を学ぶのかというと、これが現在の統計学で主流の概念である「ベイズの定理」を理解するために必要だからです。
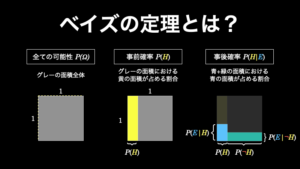
ベイズの定理とは、条件付き確率の公式を変形して導き出される以下の公式のことです。
\[\begin{eqnarray}
P(A|B)
&=&
\dfrac{P(A)P(B|A)}{P(B)}
\end{eqnarray}\]
このベイズの定理には、単に条件付き確率を変形以上の大きな意味があります。具体的には、こうすることによって以下に記している通り、公式の各パーツに重大な意味が与えられるのです。
- 事後確率 \(P(A|B)\):\(B\) という出来事を観察した上で \(A\) が起きる確率
- 事前確率 \(P(A)\):\(B\) という出来事を観察する前の段階で \(A\) が起きる確率
- 尤度(逆確率) \(P(B|A)\):\(A\) が起きた場合に \(B\) という出来事を観察することの尤もらしさ(確率と似ているが異なる概念)
- 周辺尤度 (周辺確率)\(P(B)\):\(A\) に関係なく \(B\) という出来事を観察することの尤もらしさ(確率と似ているが異なる概念)
これについては、『ベイズの定理とは?誰でも理解できるようにわかりやすく解説』で引き続き詳しく解説していきますので、ぜひご覧ください。
4. まとめ
以上、条件付き確率について解説してきました。
条件付き確率は、従属事象 B が起きた後に、別の従属事象 A が起こる確率です。そして、これは独立事象の乗法定理を改良することで求められています。ただし条件付き確率の公式は、それ単体で使うことはほとんどありません。
その本当の凄さは、「B の後に A が起こる確率 P(A|B)」から、「A の場合に B が起こる確率 P(B|A)」を求められるという点にあります。そして、そのための公式こそが「ベイズの定理」と呼ばれるものであり、確率論の世界を超えて、統計学や人工知能の分野で中心的な概念となっているものです。ベイズの定理は、今後の社会では必須の教養になり得るものです。この定理を理解できるようになるためにも、その基礎である条件付き確率を、しっかりと理解しておきましょう。



コメント