微分– category –
-

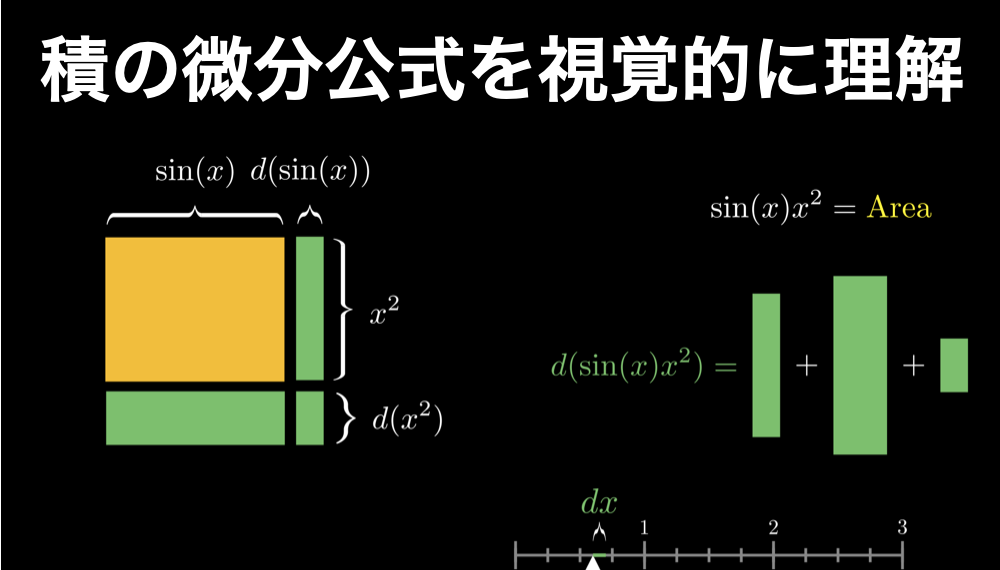
積の微分公式を誰でも直観的に理解できるように解説
積の微分公式は、関数の積の微分を求められる公式です。このページでは、これについて誰でも理解できるように解説していきます。具体的には以下の3点について深く理解できるようになります。 関数の積の簡単なおさらいできる積の微分公式を暗記に頼らずに... -

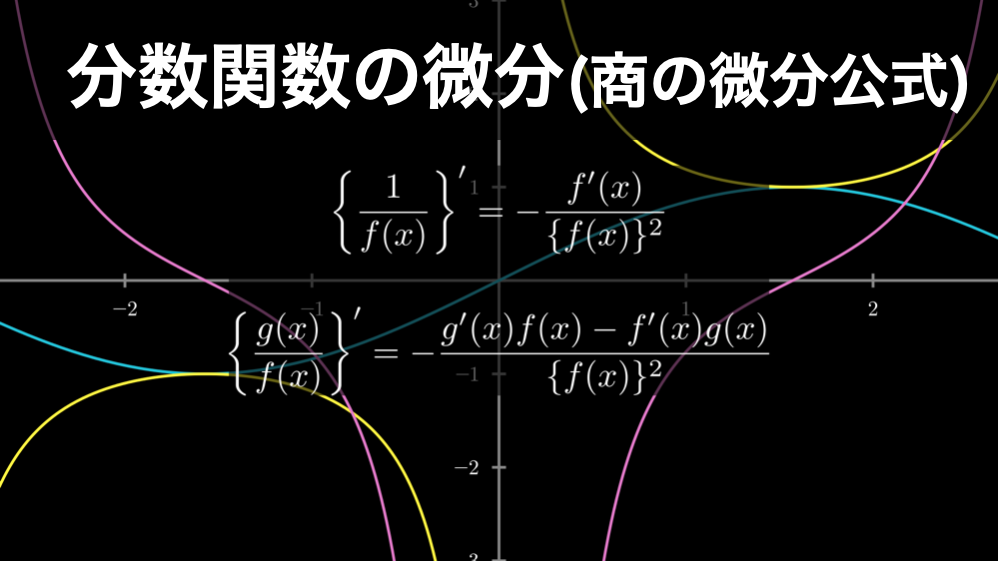
分数関数の微分のやり方(商の微分公式)を誰でもわかるように解説
分数の微分は公式を使って、簡単に解くことができます。このページでは、まず、この公式を紹介し、その後でなぜ、それらの公式で分数の微分を求めることができるのかを、誰でも理解できるように解説していきます。 特に以下のような点を深く理解することが... -

合成関数の微分を誰でも直観的かつ深く理解できるように解説
結論から言うと、合成関数の微分は (g(h(x)))' = g'(h(x))h'(x) で求めることができます。これは「連鎖律」と呼ばれ、微分学の中でも非常に重要なものです。 そこで、このページでは、実際の計算例も含めて、この合成関数の微分について誰でも深い理解を得... -

三角関数の微分を誰でも驚くほどよく分かるように解説
三角関数の微分は、物理学や経済学・統計学・コンピューター・サイエンスなどの応用数学でも必ず使われており、微分の中でも使用頻度がもっとも高いものです。 具体的には、例えば、データの合成や解析に欠かすことができませんし、有名なフーリエ変換もsi... -

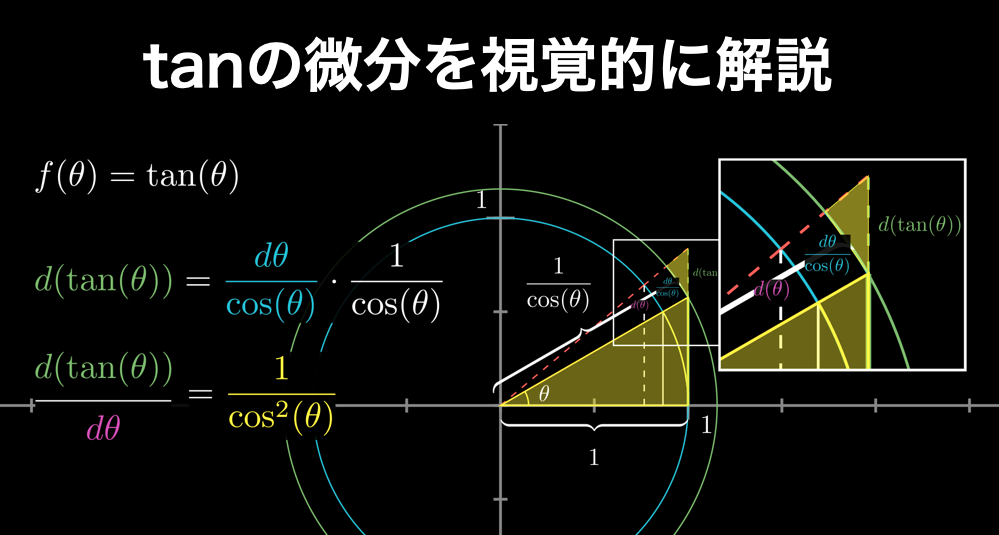
tanの微分の公式と証明が誰でも必ずわかるようになる解説
結論からお伝えすると、tan(θ)の微分は1/cos2(θ)になります。 なぜこうなるのでしょうか?その理由がわかると、単に公式を暗記するだけの場合と比べて、遥かに微分を深く理解できるようになります。そこで当ページでは、tanの微分について、誰でも理解でき... -

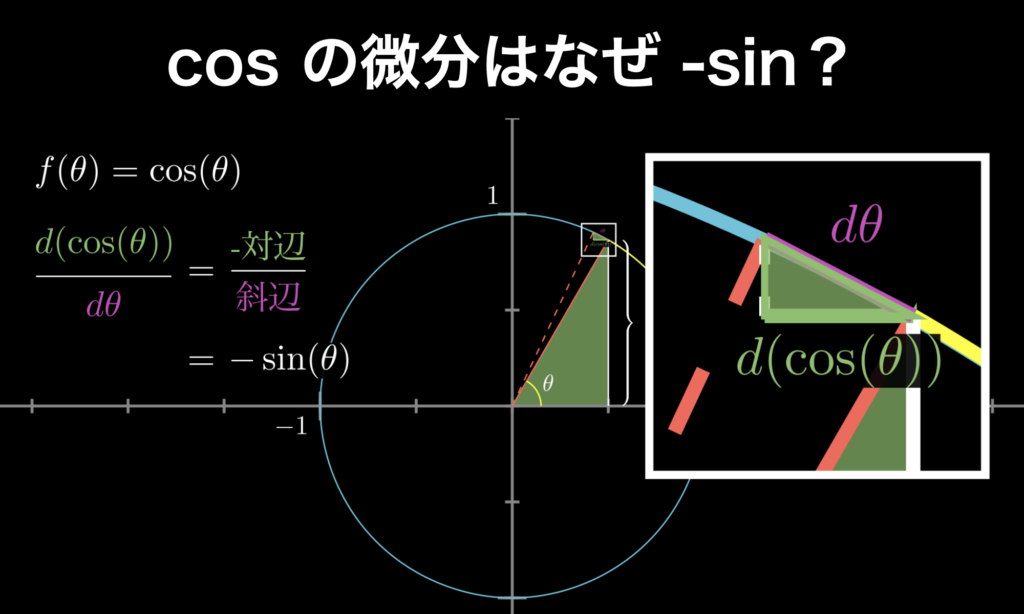
cosの微分が-sinになる理由を誰でも簡単に理解できるように解説
cos(x)を微分すると-sin(x)になります。 なぜこうなるのでしょうか?その理由がわかると、単に公式を暗記するだけの場合と比べて、遥かに微分を深く理解できるようになります。そこで当ページでは、cosの微分について、誰でも理解できるようにアニメーショ... -

sinの微分はなぜcos?誰でも直観的に理解できるように解説
三角関数の微分は、微分学の中でもずっと使うことになるとても重要なトピックです。そして結論から言うと、タイトルの通り sin の微分は cos になります。 それでは、なぜそうなるのでしょうか? 試験で高得点を取るための勉強も大切ですが、優秀なエンジ... -

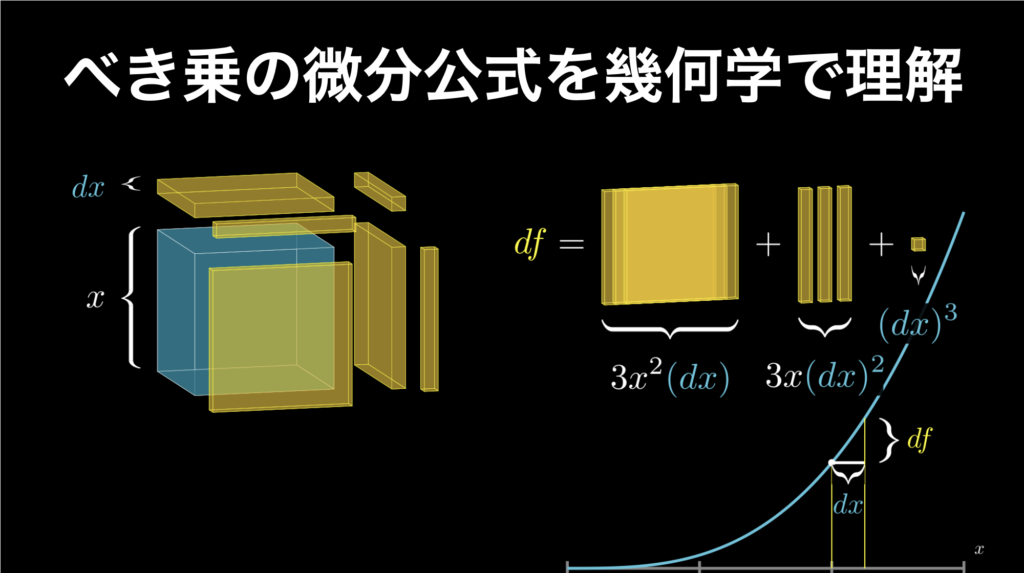
べき乗(累乗)の微分公式を誰でも必ず深く理解できるように解説
べき乗の微分・累乗の微分はどちらも同じ公式で簡単に求めることができます。その公式を知っておけば、べき乗の微分は、わざわざ微分の定義式から計算する必要なく、素早く簡単に求められるようになります。 それが以下の公式です。 なお、べき乗・累乗は... -

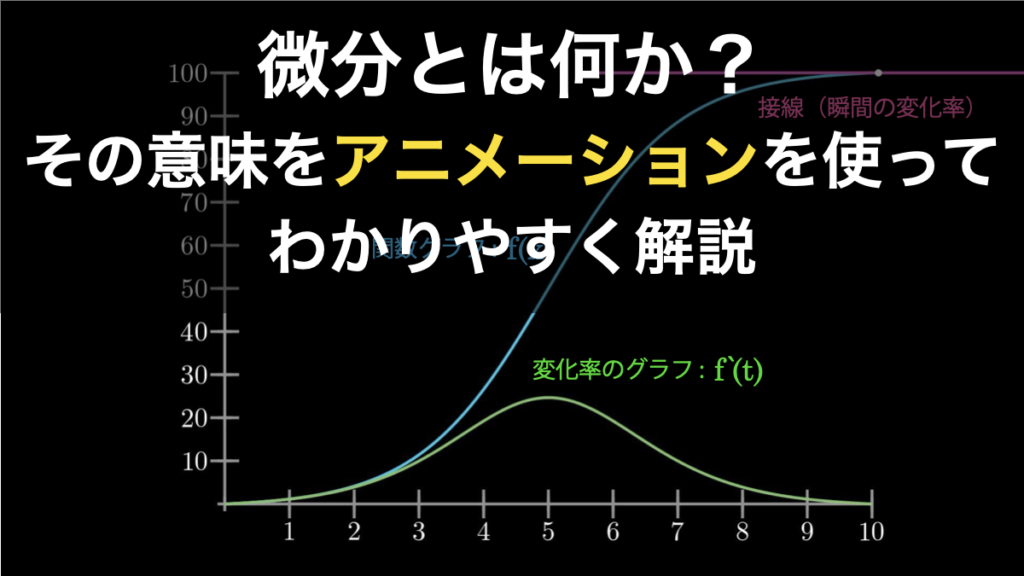
微分とは何か?わかりやすくイメージで解説
微分とは、結論から言うと「瞬間の変化率」のことであり、視覚的には「ある関数のある地点における接線の傾き」のことです。また概念的には、微分は「ある複雑な事象の全体を非常に細かいパーツに分解して、分析すること」を意味します。 そして実務におい...
12