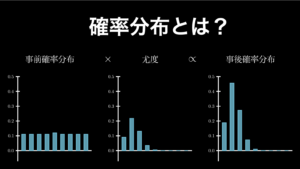
ベイズ推定は、ベイズの定理を使った統計的推定方法の一つです。具体的にはベイズの定理の確率を、確率分布に置き換えたものであり、「事前確率分布と尤度関数から、事後確率分布を求める」というものです。ちょうど、下図のようなイメージです。
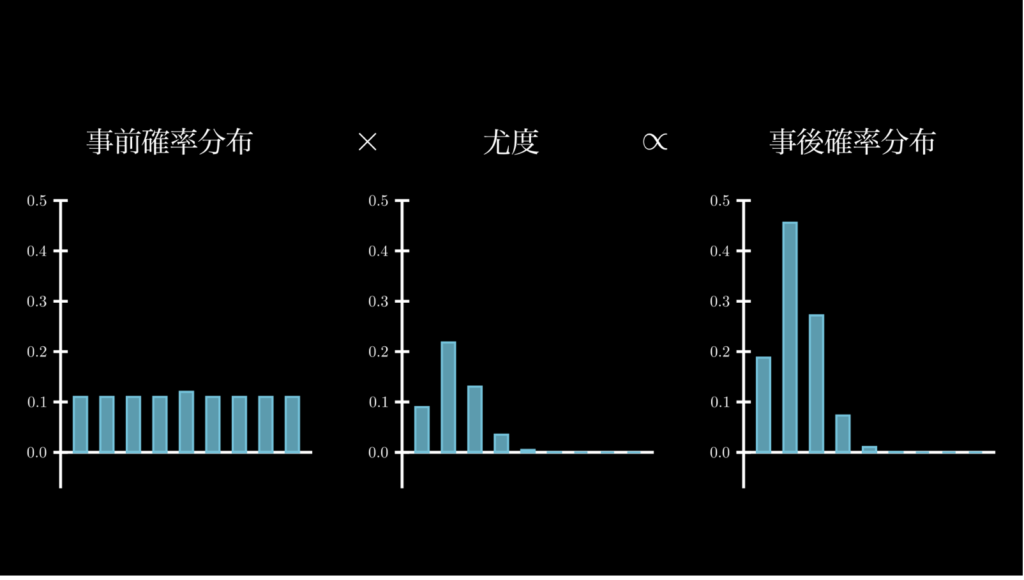
そして、ベイズ推定は、データが集まるたびに、ベイズ更新によって正確性が向上していくという素晴らしい性質を備えています。この性質ゆえ、ビッグデータが重要な現代において、科学、工学、哲学、薬学、スポーツ学、法学から、カーシェアリングといった事業まで、あらゆる分野において使われている非常に重要な概念です。当ページでは、このベイズ推定について、じっくりと解説していきます。具体的には、以下のようなことを学ぶことができます。
- ベイズ推定と従来の統計的推定の違いがハッキリとわかる:ベイズ推定と従来の統計的推定の違いについて、人に教えられるぐらい具体的にハッキリとわかります。
- 例題を見ることで、ベイズ推定と従来の統計的推定を行う方法を身につけられる:一つの簡単な例題を用意して、その例題をベイズ推定・従来の統計的推定の 2 つの方法で、丁寧に解説しながら解いています。これをご覧頂くと、2 つの推定方法を行う基本的な方法をマスターすることができます。
- 実際に練習問題を解くことで、より理解を深められる:最後にもう一つ、例題よりも簡単な練習問題を用意しています。これに実際にチャレンジして頂くことで、ベイズ推定と従来の統計的推定の理解を完璧にすることができるでしょう。
今後、ベイズ統計の学習を進める上で土台となる部分の一つなので、ぜひ、じっくり読み進めて頂ければと思います。
なお、当ページをご覧になる前に、ぜひ『確率分布とは?誰でも必ず理解できるようにわかりやすく解説』もご確認下さい。リンク先のページでは、統計推定に必須の確率分布がどういうものなのかを解説していますし、ベイズ推定について重要な点にも触れています。
1. ベイズ推定とは
ベイズ推定は、ベイズの定理を使った統計的推定方法のことです。ここでは、まず、ベイズ推定の基本的な知識として以下の 2 点を解説します。
- ベイズ推定と従来の統計的推定の違い
- ベイズ推定で使うベイズの定理
これらは以降の内容を理解するための土台となる知識なので、ぜひご覧ください。それでは解説していきます。
1.1. ベイズ推定と従来の統計的推定の違い
まずはこの点について、従来の統計的推定との違いを簡潔に解説します。
従来の統計的推定は、以下のようなステップで推定を行います。
従来の統計的推定
- 帰無仮説(偽であってほしい仮説)と対立仮説(真であってほしい仮説)を立てる
- 確率関数(確率分布)を使って p-値を求める
- p-値を有意水準と照らし合わせて、どちらの仮説が正しいかを判断する
基本的に、従来の統計的推定で行えるのは、p-値を見比べて、帰無仮説と対立仮説のどちらが真であるのかを明らかにすることだけです。しかし現在では、この p-値に頼り切った推定手法は、あまりにも帰無仮説側に有利であるし、実際には効果があるのに効果がないとバッサリ切り捨てられてしまうことがあるなどの理由から、適切ではないという認識が広まってきています(*ソース1)。
一方で、ベイズ推定は以下のようなステップで推定を行います。
従来の統計的推定
- 事前仮説として事前確率分布を設定する
- データから尤度関数(事前仮説が正しい場合に、そのデータが観察できることの尤もらしさ)を求める
- 事前確率分布と尤度関数から事後確率分布を求める
ベイズ推定は、従来の統計的推定とは違って、最終的に求めた事後確率分布を使った、さまざまな分析が可能です。たとえば、ある薬が何%の確率で効果があると考えられるのか、どれぐらいの効果があると考えられるのか、といったことも数学的に示すことができます。しかもデータが増えれば増えるほど、こうした分析の正確性が向上していきます。
だからこそ、冒頭でもお伝えした通り、コンピューターの性能の発展によってビッグデータの分析が可能になって以降、ベイズ推定は、あらゆる分野で中心的な役割を担うようになっていったのです。
1.2. ベイズ推定で使うベイズの定理
ここでベイズ推定で使う確率分布用のベイズの定理を解説しておきます。まず通常のベイズの定理は以下です。
ベイズの定理
\[\begin{eqnarray}
\overset{\small (事後確率)}{P(H|D)}
=
\dfrac{
\overset{\small (事前確率)}{P(H)}
\overset{\small (尤度)}{P(D|H)}
}
{
\underset{(周辺尤度)}{P(D)}
}
\end{eqnarray}\]
一方でベイズ推定の際は、ベイズの定理のそれぞれのパーツは以下の通り確率分布(関数)になります。
確率分布用のベイズの定理
\[\begin{eqnarray}
\overset{\small (事後確率分布)}{f(\pi|y)}
=
\dfrac{
\overset{(事前確率分布)}{f(\pi)}
\overset{(尤度関数)}{f(y|\pi)}
}
{
\underset{(一般化定数)}{f(y)}
}
\end{eqnarray}\]
まず、\(\pi\) は事前確率を意味します。そのため \(f(\pi)\) は事前確率分布を意味します。\(y\) はデータの尤度を意味します。そのため \(f(y|\pi)\) は尤度関数を意味します。最後に、\(f(y)\) は周辺尤度関数です。“関数”とついていますが、実際にはどのような変数でも同じ値を返すので定数です。ここでは、これを正規化定数と言います。正規化定数の役割は、分子の\(f(\pi)f(y|\pi)\) の総和を、確率の公理(決まりごと)を満たすために 1 にすることだけです。
具体的な使い方は、この後すぐに例題や問題の中であらためて具体的に解説していきます。ここでは、ベイズ推定においては、ベイズの定理は上記のように表されるということを覚えておいてください。
2. ベイズ推定の例題
ここでは、一つの簡単な問題を例として、従来の頻度統計の推定とベイズ推定の 2 つの手法で解いていきます。そうすることで、お互いの推定の具体的な方法と、その違いを詳しく理解することが目的です。
それでは早速、問題をご覧ください。
問題:新薬 X は有効?
新しく開発された避妊薬 X があるとします。研究者たちは、この X の効果を検証するために、クリニックに訪れた合計 40 名の女性のうち、ランダムに選ばれた 20 名に X を処方しました。この 20 名を実験グループと言うことにします。そして残りの 20 名は何の効果もないただの錠剤を与えました。こちらの 20 名を対象グループと言うことにします。結果、実験グループでは 4 名が、対照グループでは 16 名が妊娠しました。
この結果から、避妊薬 X が有効であると判断できるでしょうか?
早速、この問題を 2 つの方法で解いていきましょう。
2.1. 従来の統計推定
従来の統計推定は、次のようにアプローチしていきます。
- 帰無仮説と対立仮説を立てる
- p-値を計算する
- 有意水準で判断を下す
一つずつ見ていきましょう。
2.1.1. 帰無仮説と対立仮説を立てる
頻度統計では、最初に 2 つの仮説を立てます。帰無仮説はこの統計推定において棄却したい(偽だと証明したい)仮説のことです。そして対立仮説は採用したい(真だと証明したい)仮説のことです。当然、この問題では帰無仮説は「避妊薬 X は有効ではない」であり、対立仮説は「避妊薬 X は有効である」になります。
それでは、どのような場合に避妊薬 X は有効ではなく、どのような場合に有効であると判断できるでしょうか。これは次のように考えればわかります。
まず避妊薬 X に効果がない場合、実験グループでも対象グループでも妊娠率は変わらないということになります。そのため、被験者のうちの誰かが妊娠したときに、その誰かが実験グループに属している確率 \((p)\) と、対象グループに属している確率 \((1-p)\) はお互いに半々の 0.5 ずつになります。
一方で、避妊薬 X に効果がある場合、実験グループの方が対象グループよりも妊娠率が低いということなので、\(p<0.5\) の場合であるということがわかります。
以上のことから、帰無仮説と対立仮説はそれぞれ以下の通りになります。
- 帰無仮説 \(H_0\):\(p=0.5\) (避妊薬 X は有効ではない)
- 対立仮説 \(H_A\):\(p<0.5\) (避妊薬 X は有効である)
2.1.2. p-値を求める
それでは、帰無仮説と対立仮説ではどちらがより正しいのでしょうか。
従来の統計推定では、これを判断するための指標としてp-値を使います。p-値とは「帰無仮説が真であるという条件下において、想定される結果よりも極端な結果(=対立仮説の方に寄った結果)が出る条件付き確率」のことです。
具体的に見ていきましょう。今回、帰無仮説は「\(p=0.5\) である」 です。そのため帰無仮説が真である場合に想定される結果は、「20 人の女性 × 確率 0.5 = 10 人が妊娠する」になります。しかし、実際の結果は「 20 人の女性のうち 4 人が妊娠する」でした。帰無仮説が真であるとき(\(p=0.5\) のとき)、この結果がどれぐらいの確率で見られるものなのかを表すのが p-値です。
それでは、p-値を計算してみましょう。この問題で明らかになっているパラメータは、試行回数 20 回・成功数 4 回・成功率 0.5 なので、これらのパラメータから、この問題は二項分布に従うことがわかります。そのため p-値は、二項分布の確率質量関数で、以下の通り解くことができます。
\[\begin{eqnarray}
P(k \leq 4 | n=20, p=0.5)
&=&
\sum^4_{k=0}
\binom{20}{k}
(0.5) ^k
(1-0.5)^{20-k}\\
&=&
P(k=0 | n=20, p=0.5)+ P(k=1| n=20, p=0.5)+ \cdots + P(k=4| n=20, p=0.5)\\
&\approx&
0.0059
\end{eqnarray}\]
このように p-値は 0.0059 であることが求められました。なおこの計算に使った Python のコードは以下です。
from scipy.stats import binom
sum=0
for i in range(0,5):
sum += binom.pmf(i, 20, 0.5)
sum
2.1.3. 有意水準で判定
p-値 のこの 0.0059 という値は「帰無仮説が真であるという条件下(p=0.5であるという条件下)で、20 人中 4 名が妊娠するという結果が観察される確率は、たったの 0.59% である」ということを意味します。言い換えると p < 0.5 である確率は 100 – 0.59 = 99.41% であるということを示しています。
このことから、帰無仮説 \(H_0\) よりも対立仮説 \(H_A\) の方が正しい、つまり避妊薬 X は有効である、と非常に高い確信を持って言えます。なお一般的には、5% を境に帰無仮説を棄却できるかどうかを判断します。この判断の境界線のことを「有意水準」と言います。
以上が頻度論者の統計のアプローチです。
頻度論の統計推定の弱点
ここまで見てきたように、頻度統計は、p-値が 5 % より大きいのか小さいのかを境目に、帰無仮説が正しいのか正しくなのか白黒をつけるという方法です。ただし、この方法には問題があります。
例えば、本来は、p-値が 7% や 10 % だったとしても、避妊薬 X の効果がゼロであるという意味にはならないはずです。しかし頻度統計の推定では、こういう場合でも、有意水準を境目にバッサリと白黒をつけて、X には効果がないという結論を出すことになります。つまり、帰無仮説の方が圧倒的に有利になるのです。この点は頻度統計にとって非常に大きな問題であり、権威のある科学論文誌 Nature でも、「有意かどうかの議論はやめるべきである」という内容の記事を、多数の研究者の署名付きで発表しています(ソースを見る)。
2.2. ベイズ統計による推定
それではベイジアンは、同じ問題をどのように考えるのでしょうか?ベイジアンは、帰無仮説と対立仮説を立てるということはしません。以下のベイズの定理によって、事後確率分布を求めます(通常のベイズの定理を確率分布用に変えたものです)。
\[\begin{eqnarray}
\overset{\small (事後確率分布)}{f(\pi|y)}
=
\dfrac{
\overset{(事前確率分布)}{f(\pi)}
\overset{(尤度関数)}{f(y|\pi)}
}
{
\underset{(一般化定数)}{f(y)}
}
\end{eqnarray}\]
事後確率分布の求め方は、ベイズの定理と同じで、以下の 3 つのステップで行います(ベイズ推定では、正規化定数の計算は省略可能なため 4 つではなく 3 つになります。ただし今回の計算ではわかりやすさのため正規化定数も含めて事後確率分布を求めることにします)。
- 事前確率分布を求める
- 尤度関数を求める
- 事後確率分布を求める
それでは一つずつ見ていきましょう。
なお、確率は本来は連続値ですが、ここでは簡単化のために p の値(被験者のうちの誰かが妊娠したときに、その誰かが実験グループに属している確率)は 0.1 , 0.2 , 0.3 , … , 0.9 というように 0.1 刻みの離散値を取ることにします(=離散型確率分布を使う)。
連続型確率分布でベイス推定の計算を行う際は、考え方は同じですが、計算が極端に複雑になります。そのため「共役事前分布」という、計算が楽になる確率分布の組み合わせを使って計算をします。いずれにせよ、この連続型確率分布の場合のベイズ推定の行い方は『共役事前分布とは?誰でも理解できるようにわかりやすく解説』で解説しています。
2.2.1. 事前確率分布を求める
ベイズ推定では、事前確率分布は主観的確率を使う場合がほとんどです。
そして私たちは、最初の段階では、避妊薬 X にどれぐらいの効果があるのかまったく分からないものとします。そのため p=0.1 から p=0.9 の 9 つのモデルは同様にあり得ると考えて、事前確率は一様に 0.11 ずつ(総和を 1 にするために p=0.5 だけ 0.12 )であるとしましょう。このように事前確率がまったく検討がつかない場合に、一様分布になるように設定することは、実際にもよく行われます。
- \(f(0.1)=0.11\) * p=0.1 である確率は 0.11 であるという意味。以下同じ。
- \(f(0.2)=0.11\)
- \(f(0.3)=0.11\)
- \(f(0.4)=0.11\)
- \(f(0.5)=0.12\)
- \(f(0.6)=0.11\)
- \(f(0.7)=0.11\)
- \(f(0.8)=0.11\)
- \(f(0.9)=0.11\)
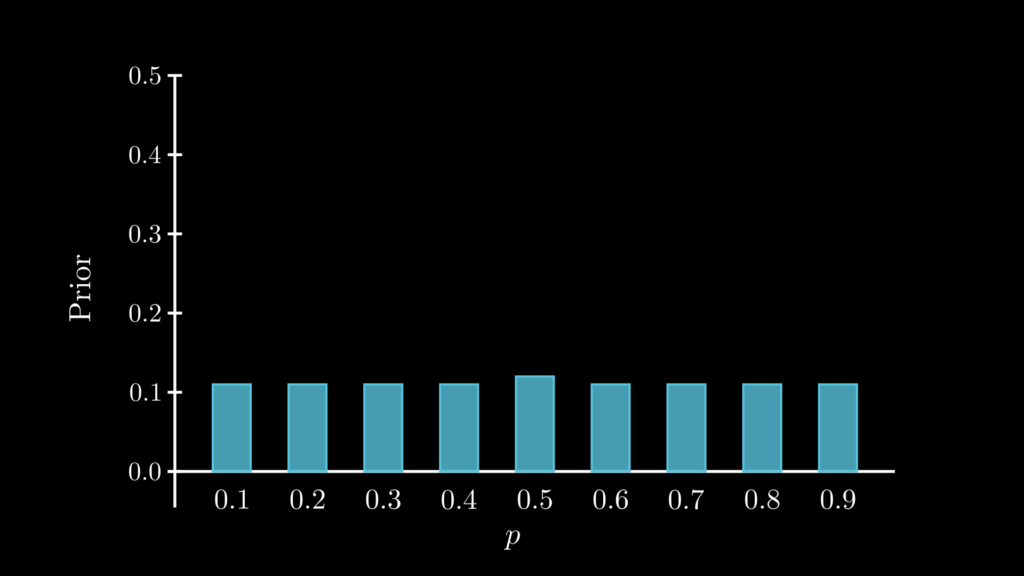
この確率分布は、事前確率はすべて同じである、つまり p=0.1 ~ p=0.9 はどれも同じようにあり得る、ということを示しています。このような分布を「一様分布」と言います(厳密には、総和を 1 にするため、p=0.5 のとことだけ 0.12 にしています)。
なお、従来の頻度統計学に慣れている方は、事前確率を直感的に設定するのは違和感があるかもしれません。しかしベイズ統計では、これは当たり前のことであり全く問題ありません。なぜなら、最初にどのように事前確率を設定したとしても、データが十分に集まれば、最終的に同じ結果が得られるからです。これについては、この章の後半でまた解説します。
2.2.2. 尤度関数を求める
次に、尤度関数を求めます。例えば、成功率 0.5 の時の尤度は、その試行を 20 回行った場合に、成功数が 4 回になる、という条件付き確率と同じですから、次の計算で求められます。
\[\begin{eqnarray}
P(k=4|n=20, p=0.5)
&=&
\binom{20}{4}(0.5)^4(1-0.5)^{16}\\
&\approx&
0.0046
\end{eqnarray}\]
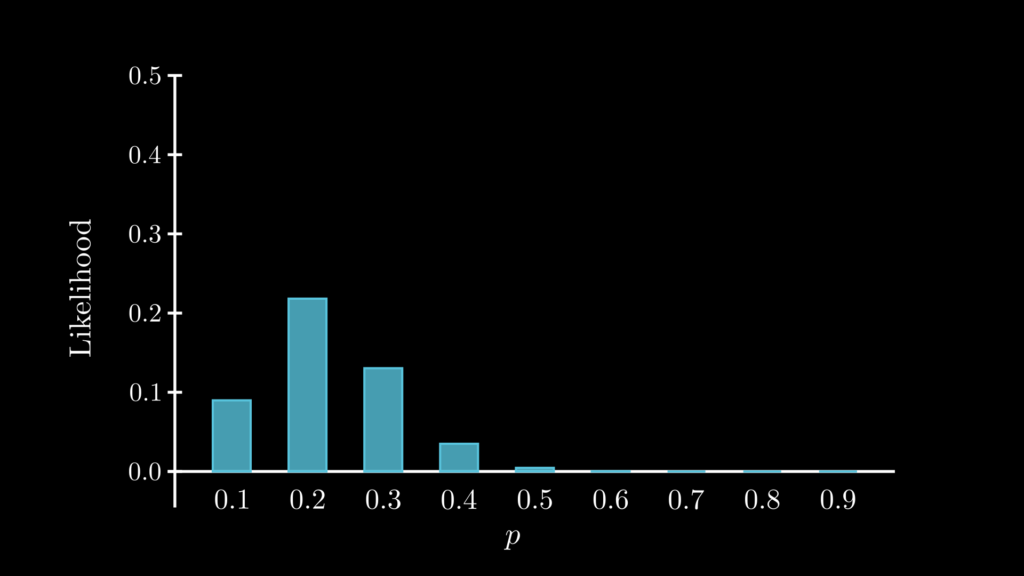
同じ計算を p=0.1 から 0.9 の値でそれぞれ行えば、以下のようにそれぞれの尤度を求められます。
from scipy.stats import binom
for i in range(1,10):
print("p=",i/10, " : ", binom.pmf(4, 20, i/10))
これらをまとめてグラフにすると、次のような尤度関数の分布が得られます。
2.2.3. 正規化定数を求める
正規化定数は、これから求める事後確率分布の確率の総和を 1 に調整するための定数です。これは、ここまで求めてきた事前確率分布と尤度関数の対応するもの同士を掛けた合計になります。
まず事前確率分布と尤度関数を下表にあらためてまとめました。
| p | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 合計 |
| 事前確率 | 0.11 | 0.11 | 0.11 | 0.11 | 0.12 | 0.11 | 0.11 | 0.11 | 0.11 | 1 |
| 尤度 | 0.090 | 0.22 | 0.13 | 0.035 | 0.0046 | 0.00027 | 0 | 0 | 0 | 0.48 |
正規化定数は、これらを列ごとに一つずつ掛けて、足し合わせたものになります。
\[\begin{eqnarray}
0.11 \cdot 0.0898
&+&
0.11 \cdot 0.2182
+
0.11 \cdot 0.1304
+
0.11 \cdot 0.035\\
&+&
0.12 \cdot 0.0046
+
0.11 \cdot 0.0003
+
0.11 \cdot 0.00
+
0.11 \cdot 0.00
&\approx&
0.053
\end{eqnarray}\]
2.2.4. 事後確率分布を求める
これで事前確率分布と尤度関数と正規化定数が求められました。ここまでで必要なものが揃ったので、ベイズの定理を使って、事後確率分布を求めることができます。
例えば p=0.5 の場合の事後確率を求めるなら以下の通りになります。
\[\begin{eqnarray}
P(n=20, p=0.5|k=4)
&=&
\dfrac
{
P(p=0.5)P(k=4|n=20,p=5)
}
{
P(k=4)
}\\
&=&
\dfrac{0.12 \cdot 0.0046}{0.053}\\
&\approx&
0.0105
\end{eqnarray}\]
これで p = 0.5 モデルの事後確率を求めることができました。これは、「20 回の試行で成功数が 4 回であるという条件下で、成功率が 0.5 である確率」は、たったの 1% であるということを示しています。
同じように p=0.1 から p=0.9 までの残りの 8 つのモデルを計算したものが、以下のコードです。
for i in range(0,9):
print("P(k=4|n=20, p=", i/10+0.10, ") : ", data[i]/sum(data))
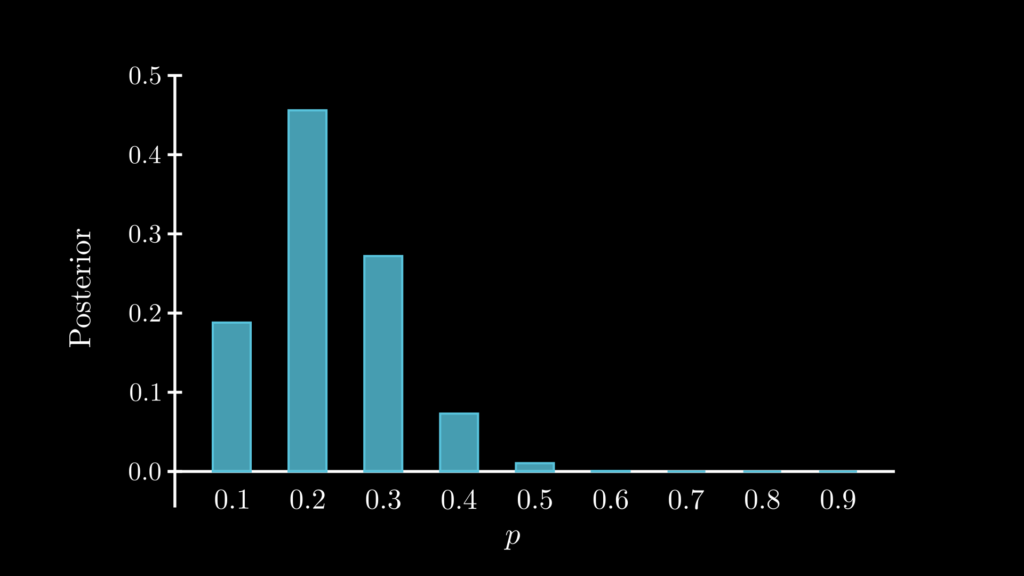
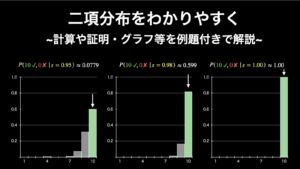
そして、これらの事後確率を棒グラフに描いたものが下図です。
2.2.5. 事後確率分布から答えを求める
事後確率分布のグラフを見れば、ほとんど 100 % の確率で p < 0.5 となることがわかります(実際は上の表より0.188 + 0.456 + 0.272 + 0.0731 = 0.989 と求められます)。要するに、避妊薬 X が有効である可能性は 98.9% もあるということです。
中でも、p=0.2 である確率が 0.456 と頭一つ抜けています。このことから、妊娠した女性が実験グループの人である確率 (0.2) は、対照グループの人である確率 (0.8) の 1/4 となる可能性(つまり避妊薬 X を摂取すると、妊娠率が 1/4 になる可能性)が最も高いということがわかります。
頻度統計の推定では、帰無仮説に対して対立仮説の方が真である可能性がどれぐらいあるのか、ということしか分かりませんでした。一方でベイズ推定では、ここまで見てきたように、確率をグラフに描けて直感的に全体を把握しやすいですし、全モデルを計算するので、より詳細な分析が可能になります。
これこそが、ベイズ統計が主流になった主な理由の一つです。
補足:事前確率分布が主観的でも問題ない理由
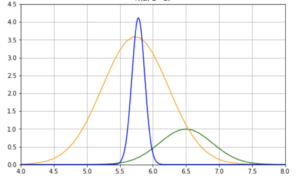
ここまで見てきたように、ベイズ統計とは、簡単に言うと、事前確率分布(Prior)と尤度(Likelihood)から、事後確率分布(Posterior)を求めるというものです。下図はこれを視覚的に表したものです。
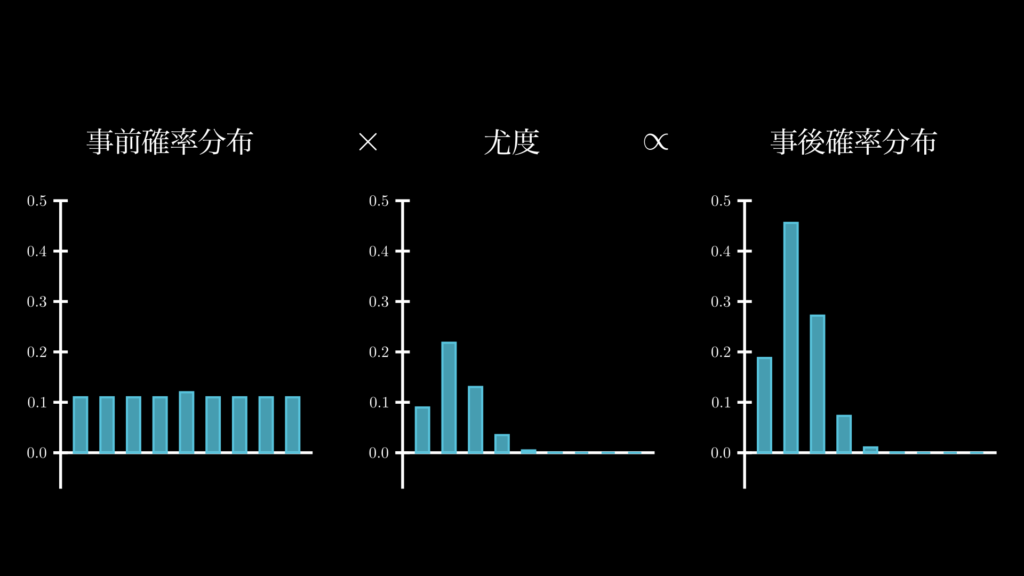
それでは、データサイズが倍の n=40, k=8 になったらどうなるでしょうか。この場合は、下図のようになります。
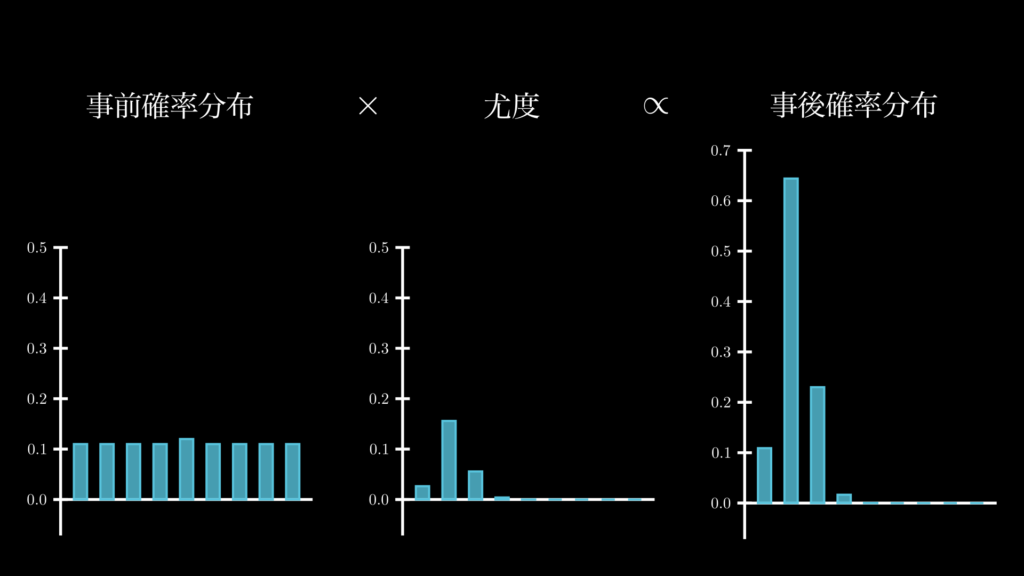
まず事前確率分布は変わりません。尤度は p=0.2 が頂点であることは変わりませんが、横幅が狭くなっていることがわかります。この事前確率分布と尤度から、求められた事後確率分布を見てみると、尤度と同じように横幅が狭くなっているのはもちろん、p=0.2 の確率が大きく伸びたのと同時に、それ以外の確率が下がったことが分かります。
データサイズが大きくなるほど、この傾向は強くなります。例えば、n=200, k=40 になれば、尤度と事後確率分布は下図の通りになります。
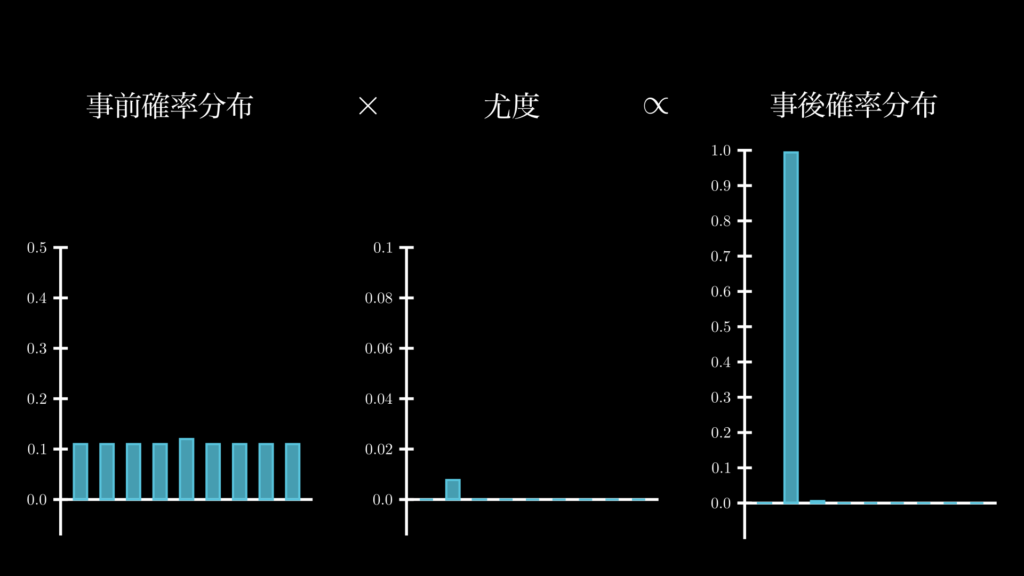
このように今度は p=0.2 である確率が 99% 以上になっていることがわかります。
以上の点から次のような重要ポイントを見出すことができます。
- データが増えれば増えるほど、事後確率分布はどんどん正確になっていく
- データが十分に大きくなると、事前確率分布はほとんど全く問題なくなる
2 つ目のポイントについて補足しておきます。ベイズ統計では、事前確率として主観的確率を用いるという点に抵抗を感じる人がいます。これは厳密な数学が好きな方に多い傾向です。しかし、データが十分に集まれば、結局、事前確率分布の計算に占める割合は、無視して良いほど微々たるものになるのです。
新しいデータを正しく解釈することで、事前に持っていた信念を、より現実に即した事後信念に変えていくということが重要なのです。そして、これこそがベイズ統計の本質です。
3. ベイズ推定の練習問題
最後に、ベイズ統計 vs. 頻度統計の練習問題に、是非チャレンジしてみてください。この章をご覧頂いたら、ここまでお伝えしてきたことが、より腑に落ちて、スッキリします。
それでは早速、以下の問題をご覧ください。
問題:新米コンサルタント
W 社は、1 パックの中に赤・緑・黄・青・橙の 5 色のマーブルチョコレートがランダムに入った商品 W&W’s を販売しています。1 パックには 合計 5 個のマーブルチョコレートが入っています。今、ライバルの X 社は、W&W’s の母集団の中の黄色のマーブルの割合は 10% か 20% であるというところまで突き止めました。あるコンサルタントは、これが実際に 10% なのか 20% なのかを決定するための統計コンサルタントとして X 社に雇われました。
このコンサルタントは初仕事として、正しい決断を下すように求められています。もし正しい決断をしたらボーナスを貰えます。しかし、決断を間違えたら仕事を失うことになります。
コンサルタントには、調査のための W&W’s の購入予算として、4000 ドルが割り当てられています。1 パック 1000 ドルなので、合計で 4 パック(マーブルチョコレート 20 個分)まで購入できます。
間違った決断を下すコストはとても高いので、コンサルタントは自信のある状態で決断を下したいと考えています。しかしデータ収集もコストがかかります。そのため必要以上にデータを買いたくはありません。もし、小さなサンプルサイズで正しい決断ができるなら、そうすることで支出をセーブしたいと考えています。
この状況で正しい決断をしてください。
なお、W&W’s を買った時の黄色のマーブルチョコレートの割合はそれぞれ以下の通りになるとします。
- 1 パック:k=1, n=5
- 2 パック:k=2, n=10
- 3 パック:k=3, n=15
- 4 パック:k=4, n=20
これを従来の統計のアプローチと、ベイズ統計のアプローチで解いてみてください。答えは以下で解説しています。
3.1. 従来の統計推定の答え
まずは雇われたコンサルタントが頻度論者だった場合を考えてみましょう。まずは、このコンサルタントは調査のために 1 パックだけ買ったとします。
従来の統計推定では、まず 2 つの仮説を立てます。
- 帰無仮説 \(H_0\):p=0.1
- 対立仮説 \(H_A\):p>0.1
1 パックを調べた場合のデータは k=1, n=5 なので p-値は次のように計算できます。
\[\begin{eqnarray}
P(k \geq 1 | n=5,p=0.10)
&=&
P(k=1 | n=5,p=0.10)+ \cdots + P(k=5 | n=5,p=0.10)\\
&=&
1-P(k=0|n=5,p=0.10)\\
&=&
\binom{5}{0}(1-0.90)^5
\approx 0.41
\end{eqnarray}\]
以上のことから、帰無仮説を棄却できないことになり、このコンサルタントは「 10% が正しい」という決断を下すことになります。
それでは新たなデータを購入していった場合は、p-値はどうなるでしょうか。次のようになります(計算式は省略します)。
- n=5, k=1:0.41
- n=10, k=2:0.26
- n=15, k=3:0.18
- n=20, k=4:0.13
このように 4 パック最大までデータを購入しても、p-値が有意水準 (0.05) を満たすことはありません。そのため頻度論者のコンサルタントは、最後まで 10% の方を選ぶことになります。
一見するとこれは不可解な決断であることがわかります。なぜなら、p-値が 0.05 以下にならないとは言えど、確実にそちらに近づいていっているからです。つまり、データが増えれば増えるほど、20 % の選択が正しいという方向へ近づいているのです。それでも、頻度統計の判断基準は、p-値が有意水準を下回るかどうかなので、頻度論者のコンサルタントは、どの場合でも、正しい割合は 10% であるという決断をすることになります。
3.2. ベイズ統計の答え
次に、この新人コンサルタントがベイジアンだったとします。その場合、彼は次のように問題にアプローチします。
まず、今回あり得るパターンは p=0.1 か p=0.2 だけなので、次の 2 つのモデルをそれぞれ計算することになります。
- モデル1 \(H_1\):p=0.1
- モデル2 \(H_2\):p=0.2
続いて事前確率を設定します。事前に何のデータもないので、\(H_1\) が真である確率も、\(H_2\) が真である確率も同じであろうと考え、\(P(H_1)=\)\(P(H_2)\)\(=0.5\) とします。
- 事前確率 \(P(H_1)=P(H_2)=0.5\)
続いて、尤度を求めます。
- 尤度1 \(P(k=1|H_1) = \binom{5}{1}(0.10)(0.90^4) \approx 0.33 \)
- 尤度2 \(P(k=1|H_2) = \binom{5}{1}(0.20)(0.80^4) \approx 0.41 \)
これで事後確率を求めることができます。
- 事後確率1 \(P(H_1|k=1)=\dfrac{P(H_1)P(k=1|H_1)}{P(k=1)}=\dfrac{0.5 \times 0.33}{0.5 \times 0.33 + 0.5 \times 0.41} \approx 0.45\)
- 事後確率2 \(P(H_2|k=1)=1-0.45=0.55\)
結果、\(H_1\) の事後確率と \(H_2\) の事後確率は似通っており、このデータサイズでは正しい決断を下すことが難しいと判断できます。それでも、この時点で決断を下さないといけないとしたら、\(H_2\) の方がまだ事後確率が高いので、20 % と決断することでしょう。
それではデータサイズを増やすとどうなるでしょうか?それぞれの場合の事後確率計算して、まとめたものが以下です(計算は省略します)。
| ベイズ \(H_1\) | ベイズ\(H_2\) | |
| 観察データ | P(p=0.10 | n, k) | P(p=0.20 |n,k) |
| n=5,k=1 | 0.45 | 0.55 |
| n=10, k=2 | 0.39 | 0.61 |
| n=15, k=3 | 0.34 | 0.66 |
| n=20, k=4 | 0.29 | 0.71 |
このようにデータが増えるごとに、\(H_1\) が真である確率が下がり、反対に \(H_2\) が真である確率が上がります。
以上のことから、一貫して 10% に固執し続けた頻度論者のコンサルタントと異なり、ベイジアンのコンサルタントは一貫して 20% と決断することになります。より正確な判断をするには、さらに多くのデータが必要ではありますが、ベイジアン・コンサルタントの決断が正しい可能性の方が高いと言えます。
3.3. ベイズ統計と従来の統計推定の違いまとめ
ここまでで、ベイズ統計と頻度統計では、ベイズ統計の方がより柔軟で正しい可能性が高い決断ができることが理解できたと思います。あらためて、両者の統計手法的な違いを簡潔にまとめると以下の通りです。
頻度論統計
- 帰無仮説と対立仮説のどちらがあり得るかの推定しかできない
- 帰無仮説の方が圧倒的に有利になってしまう
- 計算が楽
ベイズ統計
- 全てのモデルを計算して推定する
- モデル間の様々な分析が可能になる
- 手計算ではほとんど不可能
まとめるとベイズ統計は非常に優れた意思決定・判断決定ツールだと結論できます。もちろんベイズ統計にもデメリットはあります。それは、手計算が不可能なほどに計算が複雑になるということです。しかし、今ではコンピューターの処理能力が飛躍的に向上したおかげで、このデメリットはなくなっています。というよりも、コンピューターの発達によって、あっという間に演算できるようになったことが、ベイズ統計を蘇らせた主要因です。
4. まとめ
最後に内容をまとめておきます。
ベイズ推定とは
ベイズ推定とは、ベイズの定理を使った統計的推定方法のことです。ベイズ更新ができるという性質から、ビッグデータが重要な現代において、統計学のメインの地位を占めるようになっています。
ベイズ推定と従来の統計的推定の違い
従来の統計的推定は、①帰無仮説と対立仮説を立てて、② p-値を求め、③ p-値を有意水準と照らし合わせて、帰無仮説と対立仮説のどちらが正しいかを決めるという方法です。
一方でベイズ推定は、①事前確率分布を作り、②尤度関数を求め、③事後確率分布を求めるという方法です。従来の統計的推定のように、2 つの仮説だけを比べる方法ではありません。事後確率分布を見ることで、様々な分析が可能になり、どう判断するのが、統計的に最も合理的なのかを、多角的に判断することができます。
従来の統計的推定のメリットは、計算の簡単さにあります。電卓は必要かもしれませんが、コンピューターがなくても問題なく行えます。一方で、デメリットは、帰無仮説が非常に有利な点が挙げられます。また、帰無仮説と対立仮説のどちらが正しいのかを白黒つけるという融通の効かないものなので、専門家からも大きな懸念の声が上がっています。
ベイズ推定のメリットは、従来の統計的推定のデメリットを補うのはもちろんですが、それ以上に、現在のビッグデータの時代は、データを簡単に大量に集めて、そして大量の計算を素早く行えるようになったため、非常に正確な事後確率を得られるという点にあります。デメリットは、計算が複雑で手計算ではまず不可能という点が挙げられます。ベイズ推定を行うには、電卓だけでは不十分で、プログラミングのスキルが求められます。
以上がベイズ推定のまとめです。最後までご覧頂きありがとうございます。
当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります(コメント返信は余裕ができれば行いたいと考えています)。

コメント