当ページでは、arcsinの微分公式について、誰でもわかるように、幾何学的なイメージを用いて解説していきます。
なお arcsin について理解するには、 sin 関数と逆関数についての理解が必要です。それぞれ以下で解説していますので、ぜひご確認ください。
それでは始めましょう。
1. arcsin とは
最初に arcsin について確認しておきましょう。
arcsin は sin の逆関数であり、sin-1 と表記されることもあります。つまり、以下の画像で示している通り、この二つの関数は \(y=\sin(\theta) \ \leftrightarrow \ \theta=\arcsin(y)\) という関係にあります。
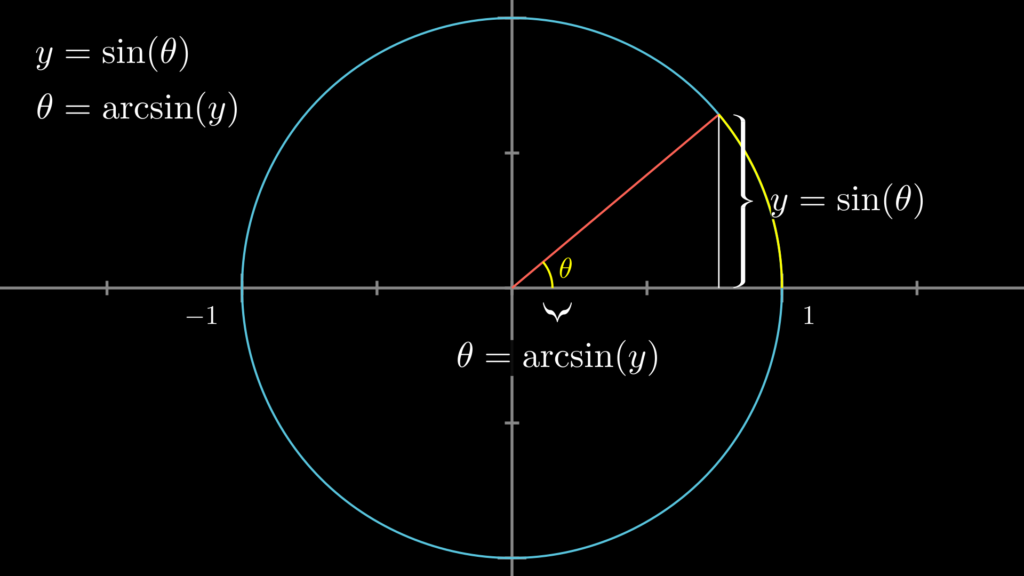
このように、arcsin に sin の値を入力すると \(\theta\)（ラジアン）を取得することができます。
そして、これらの関数をグラフで描くと、それぞれ以下のような曲線を描きます。ご覧の通り、sin の値域（sin の出力値の範囲）は \(-1 \leqq y \leqq 1\) なので、その逆関数である arcsin の定義域（arcsin への入力値の範囲）も \(-1 \leqq x \leqq 1\) になります。
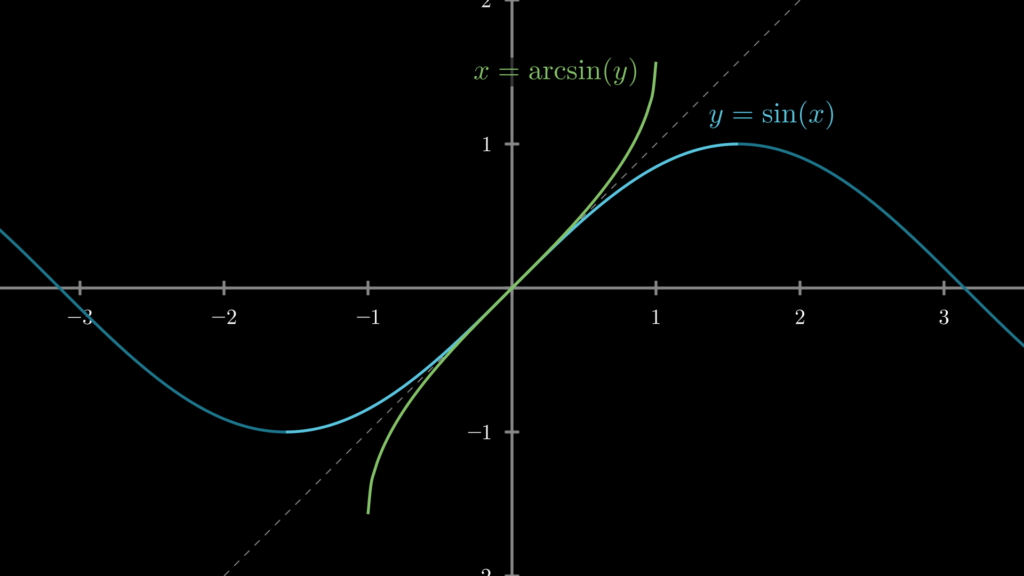
なお、arcsin と三角関数の関係については、以下を知っておきましょう。
arcsin と三角関数の関係
- \(\sin(\arcsin x)=x\)
- \(\cos(\arcsin x)=\sqrt{1-x^2}\)
- \(\tan(\arcsin x)=\dfrac{x}{\sqrt{1-x^2}}\)
これらは暗記する必要はありません。以下の画像のように、単位円上のラジアンが \(\theta\)、半径が \(1\) の直角三角形をイメージすると、ピタゴラスの定理から簡単に求めることができます。
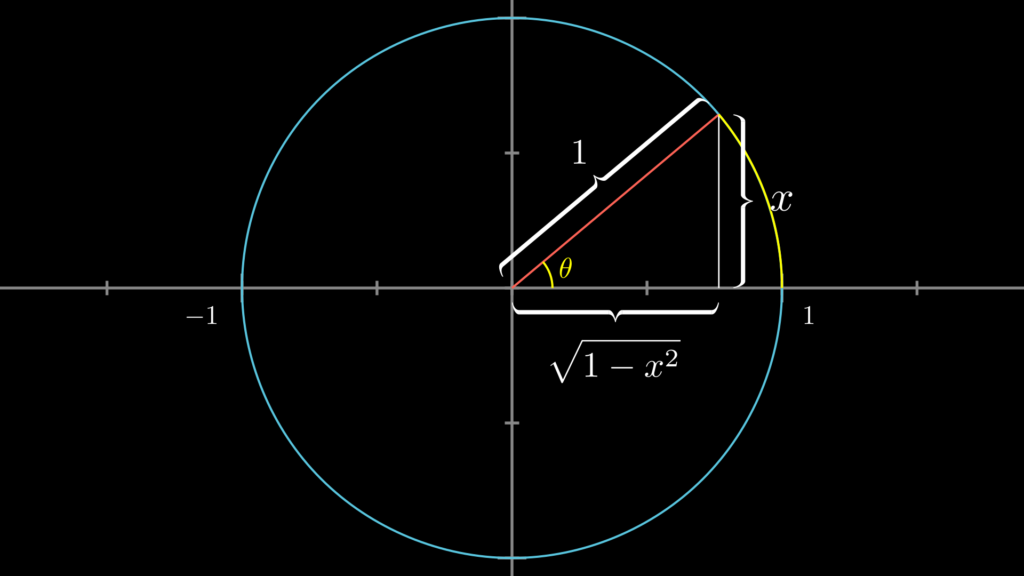
2. arcsin の微分
それでは、arcsin の微分はどうなるでしょうか。結論から言うと、以下の通りになります。
arcsin の微分
\[
\arcsin^{\prime}(x)=\dfrac{1}{\sqrt{1-x^2}}
\]
なぜこうなるのかは、arcsin が sin の逆関数であることを考えれば、簡単に理解することができます。
\(y=\sin(x)\)のとき、\(x=\arcsin(y)\) です。そのため、\(\arcsin^{\prime}(y)\) は、逆関数の微分公式より、以下のように求められます。
arcsin の微分の証明（逆関数の微分公式より）
\[\begin{eqnarray}
\arcsin^{\prime}(y)
&=&
\dfrac{1}{\sin^{\prime}(x)}\\
&=&
\dfrac{1}{\cos(x)}\\
\end{eqnarray}\]
これは \(\arcsin^{\prime}(y)=\arcsin^{\prime}(\sin(x))\) なので \(\arcsin^{\prime}(x)\) に変換します。そのために は 双方の \(x\) を \(\arcsin(x)\) に変換します。
\[\begin{eqnarray}
\arcsin^{\prime}(\sin(x))
&=&
\dfrac{1}{\cos(x)}\\
\rightarrow
\arcsin^{\prime}(\sin(\arcsin(x)))
&=&
\dfrac{1}{\cos(\arcsin(x))}\\
\rightarrow{}
\arcsin^{\prime}(x)
&=&
\dfrac{1}{\sqrt{1-x^2}}
\end{eqnarray}\]
以上。
3. arcsinの微分まとめ
以上が arcsin の微分です。
文中でお伝えした通り、これは暗記しようとする必要はありません。三角関数の微分と逆関数の微分をしっかりと理解していれば、暗記していなくても簡単に導き出すことができるからです。
ピンと来ない場合は、以下の２つのページで、あらためて微分の基本をしっかりと理解するようにしましょう。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント