Generator.waldは、ワルド分布(逆ガウス分布)から乱数配列を生成するジェネレータメソッドです。
ワルド分布は逆ガウス分布としても知られており、広がり(scale)が無限に近づくほど、ガウス分布に近づいていきます。ただし、いくつかの文献では、ワルド分布は平均値1の逆ガウス分布だとされていますが、これは普遍的な法則ではありません。
逆ガウス分布は、ブラウン運動との関係で研究された分布です。逆ガウス分布という名前がついているのは、一定距離にかかる時間と、時間当たりの距離には、逆相関関係があるからです。
ワルド分布(逆ガウス分布)は、ワイブル分布と並んで、株式収益率や利子率のモデリングに使われます。
このページではワルド分布から乱数配列を生成するGenerator.waldについて解説します。
1. 書式
書き方:
Generator.wald(mean, scale, size=None)
パラメーター:
| mean: float or array_like of floats 平均値(>0) |
| scale: float or array_like of floats 広がり(>0) |
| size: int or tuple of ints, optional 出力する配列のshape。(m, n, k)を渡すと、shape(m, n, k)の乱数配列を生成する。デフォルト値Noneで、mean, scaleがスカラーの場合は1つの乱数の値を返す。それ以外の場合はnp.broadcast(mean, scale).sizeの乱数配列を返す。 |
戻り値:
| out: ndarray or scalar パラメータを設定したワルド分布から乱数配列を生成。 |
Notes
ワルド分布の確率密度関数は次の通りです。
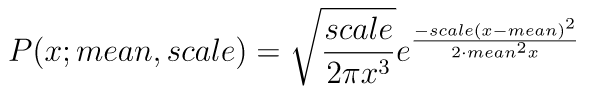
2. サンプルコード
それでは、サンプルコードを見ていきましょう。
まずは、random.default_rng コンストラクタでジェネレータオブジェクトを作成します。『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』に目を通しておいてください。
import numpy as np
rng = np.random.default_rng()
rng
こうして作成したジェネレータオブジェクト rng に対して、Generator.waldを呼び出すことによって、ワルド分布から乱数配列を取得することができます。
第一引数に中央値mean、第二引数に広がりscale、第三引数に配列のsizeを渡します。
rng.wald(3, 2, 5)
以下に平均値meanが10で、広がりscaleが異なるワルド分布を描いています。scaleが大きくなるほど、正規分布に近づいていきます。
import matplotlib.pyplot as plt
plt.subplot(221)
h = plt.hist(rng.wald(10, 1, 100000), bins=200, density=True)
plt.title('mean=10, scale=1', fontsize=12)
plt.subplot(222)
h = plt.hist(rng.wald(10, 10, 100000), bins=200, density=True)
plt.title('mean=10, scale=10', fontsize=12)
plt.subplot(223)
h = plt.hist(rng.wald(10, 100, 100000), bins=200, density=True)
plt.title('mean=10, scale=100', fontsize=12)
plt.subplot(224)
h = plt.hist(rng.wald(10, 1000, 100000), bins=200, density=True)
plt.title('mean=10, scale=1000', fontsize=12)
plt.tight_layout()
plt.show()
3. まとめ
以上、Generator.waldはワルド分布から乱数配列を生成するジェネレータメソッドです。
以前は、numpy.random.wald関数が使われていましたが、ジェネレータメソッドを使うようにしましょう。こちらの方が、処理が高速で、大量のデータを扱う科学技術計算に適しているからです。

コメント