Generator.standard_cauchyは、標準コーシー分布(最頻値mode=0)から乱数配列を生成するジェネレータメソッドです。
コーシー分布は、調和振動子問題の解決策として、またスペクトル線の広がりを示す分布として生まれました。この分布は、ガウス分布よりも裾が重い形状をしています。
そのため正規性を仮定する仮説検定の研究において、コーシー分布からのデータによるパフォーマンスの計測は良い指標となります。
このページでは、この標準コーシー分布から乱数配列を生成するGenerator.standard_cauchyについて解説します。
1. 書式
書き方:
Generator.standard_cauchy(size=None)
パラメーター:
| size: int or tuple of ints, optional 出力する配列のshape。(m, n, k)を渡すと、shape(m, n, k)の乱数配列を生成する。デフォルト値Noneでは1つの乱数の値を返す。 |
戻り値:
| out: ndarray or scalar 標準コーシー分布から乱数配列を取得 |
Notes
コーシー分布の確率密度関数は次の通りです。
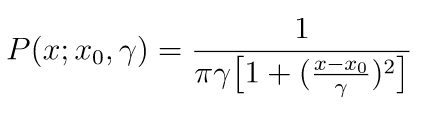
標準コーシー分布では、x0=0、γ=1に設定します。
2. サンプルコード
それでは、サンプルコードを見ていきましょう。
まずは、random.default_rng コンストラクタでジェネレータオブジェクトを作成します。『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』に目を通しておいてください。
import numpy as np
rng = np.random.default_rng()
rng
こうして作成したジェネレータオブジェクト rng に対して、Generator.standard_cauchyを呼び出すことによって、標準コーシー分布から乱数配列を取得することができます。
引数には、出力する配列のsizeを指定します。
rng.standard_cauchy(5)
以下で、標準コーシー分布のヒストグラムを描画しているので確認しましょう。
import matplotlib.pyplot as plt
s = rng.standard_cauchy(1000000)
s = s[(s>-25) & (s<25)] # truncate distribution so it plots well
plt.hist(s, bins=100)
plt.show()
標準コーシー分布はこのような形状をしています。
3. まとめ
以上のように、Generator.standard_cauchyは、標準コーシー分布から乱数配列を生成するジェネレータメソッドです。
以前は、numpy.random.standard_cauchy関数が使われていましたが、ジェネレータメソッドを使うようにしましょう。こちらの方が、処理が高速で、大量のデータを扱う科学技術計算に適しているからです。

コメント