Generator.powerは、ベキ分布から乱数配列を生成するジェネレータメソッドです。
ベキ分布は、パレート分布の逆です。またベータ分布の特別なケースであるとも言えます。金融・経済・自然界など、非常に様々な現象を示す分布と考えられており、例えば、過剰な保険金請求のモデル化などに使われます。
なお、パレート分布とベータ分布は、それぞれ以下のページで解説しています。
このページではベキ分布から乱数配列を生成するGenerator.powerについて解説します。
目次
1. 書式
Generator.power
書き方:
Generator.power(a, size=None)
パラメーター:
| a: float or array_like of floats 分布のパラメータ |
| size: int or tuple of ints, optional 出力する配列のshape。(m, n, k)を渡すと、shape(m, n, k)の乱数配列を生成する。デフォルト値Noneで、aがスカラーの場合は1つの乱数の値を返す。それ以外の場合はnp.array(a).sizeの乱数配列を返す。 |
戻り値:
| out: ndarray or scalar パラメータを設定したベキ分布から乱数配列を生成。 |
例外：
| ValueError a <1 の場合 |
Notes
ベキ分布の確率密度関数は次の通りです。
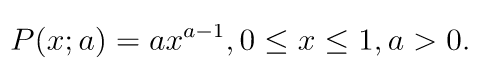
2. サンプルコード
それでは、サンプルコードを見ていきましょう。
まずは、random.default_rng コンストラクタでジェネレータオブジェクトを作成します。『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』に目を通しておいてください。
In [1]:
import numpy as np
rng = np.random.default_rng()
rng
Out[1]:
こうして作成したジェネレータオブジェクト rng に対して、Generator.powerを呼び出すことによって、ベキ分布から乱数配列を取得することができます。
第一引数は分布のパラメータα、第二引数は出力する配列のsizeです。
In [2]:
rng.power(5., 3)
Out[2]:
取得した乱数のヒストグラムと確率密度関数を描画してみましょう。
In [3]:
a = 5.
samples = 10000
s = rng.power(a, samples)
import matplotlib.pyplot as plt
count, bins, ignored = plt.hist(s, bins=30)
x = np.linspace(0, 1, 100)
y = a*x**(a-1.)
normed_y = samples*np.diff(bins)[0]*y
plt.plot(x, normed_y)
plt.show()
冒頭で伝えた通り、ベキ分布はパレート分布と真逆の関数です。以下に描画しておきます。
In [4]:
import matplotlib.pyplot as plt
rvs = rng.power(5, 1000000)
rvsp = rng.pareto(5, 1000000)
xx = np.linspace(0,1,100)
# ベキ分布
plt.subplot(211)
plt.hist(rvs, bins=50, density=True)
plt.plot(xx,powpdf,'r-')
plt.title('power(5)')
# 逆パレート分布
plt.subplot(212)
plt.hist(1./(1.+rvsp), bins=50, density=True)
plt.plot(xx,powpdf,'r-')
plt.title('inverse of 1 + Generator.pareto(5)')
plt.tight_layout()
plt.show()
3.まとめ
以上のように、Generator.powerは、ベキ分布から乱数配列を生成するジェネレータメソッドです。
以前は、numpy.random.power関数が使われていましたが、ジェネレータメソッドを使うようにしましょう。こちらの方が、処理が高速で、大量のデータを扱う科学技術計算に適しているからです。
：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。
コメント