Generator.paretoは、パレート分布(厳密にはパレートⅡ分布)から乱数配列を生成するジェネレータメソッドです。
パレート分布は80-20ルールとして広く知られています。よく聞くのは業績の80%を全体のたった20%の人々が上げており、残りの80%の人々は20%の業績しか上げていないというものです。このべき乗確率分布は、現実の数々の問題に使われています。例えば、富の配分の分布、保険に関する統計の分布、油田サイズの分布などです。
このページではパレート分布から乱数配列を生成するGenerator.paretoについて解説します。
1. 書式
書き方:
Generator.pareto(a, size=None)
パラメーター:
| a: float or array_like of floats 分布の形状 |
| size: int or tuple of ints, optional 出力する配列のshape。(m, n, k)を渡すと、shape(m, n, k)の乱数配列を生成する。デフォルト値Noneで、aがスカラーの場合は1つの乱数の値を返す。それ以外の場合は、np.array(a).sizeの乱数配列を返す。 |
戻り値:
| out: ndarray or scalar パラメータを設定したパレート分布から乱数配列を生成。 |
Notes
厳密に言うと、Generator.paretoは指定の形状のパレートⅡ(または「ロマックス分布」)から乱数を取得します。クラシカルなパレート分布は、ロマックス分布に1を足して、スケールのパラメータmを掛けることで得られます。パレート分布の確率密度関数は次の通りです。
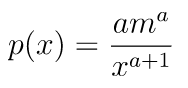
αがshapeで、mがスケールです。
ロマックス分布の最小値は0ですが、クラシカルなパレート分布の最小値はμです。標準的なパレート分布のそれはμ=1です。またロマックス分布は、一般化パレート分布(SciPyで使うことができます)のscaleを1、locを0に設定した単純化バージョンとも考えられます。
パレート分布は0より大きくなければならず、上限値は無制限です。
2. サンプルコード
それでは、サンプルコードを見ていきましょう。
まずは、random.default_rng コンストラクタでジェネレータオブジェクトを作成します。『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』に目を通しておいてください。
import numpy as np
rng = np.random.default_rng()
rng
こうして作成したジェネレータオブジェクト rng に対して、Generator.paretoを呼び出すことによって、パレート分布から乱数配列を取得することができます。
なお、このジェネレータメソッドは、パレートⅡ分布(ロマックス分布)の乱数配列を生成します。
# パレートⅡ分布(ロマックス分布)の乱数配列を生成
rng.pareto(3. ,10)
クラシカルなパレート分布の乱数配列を取得したい場合は、次のように書きます。
# クラシカルなパレート分布の乱数配列を生成
a, m = 3., 2.
s = (rng.pareto(a, 10000) + 1) * m
s
これのヒストグラムと確率密度関数を描いてみましょう。
# クラシカルなパレート分布(最小値μ)
# のヒストグラムと確率密度関数
a, m = 3., 2. # shape and mode
s = (rng.pareto(a, 10000) + 1) * m
import matplotlib.pyplot as plt
count, bins, _ = plt.hist(s, 100, density=True)
fit = a*m**a / bins**(a+1)
plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='r')
plt.show()
3.まとめ
以上のように、Generator.paretoは、パレート分布から乱数配列を生成するジェネレータメソッドです。
以前は、numpy.random.pareto関数が使われていましたが、ジェネレータメソッドを使うようにしましょう。こちらの方が、処理が高速で、大量のデータを扱う科学技術計算に適しているからです。

コメント