Generator.binomial は、NumPyで二項分布から乱数配列を生成するための、randomモジュールのジェネレータメソッドです。
二項分布とは、互いに独立したベルヌーイ試行(結果が成功か失敗のいずれかである試行)をn回行ったときの、成功回数を描いた離散確率分布です。
このページでは、このGenerator.binomialについて解説します。なお、同じ操作をするのに今までは、np.random.binomial関数を使っていましたが、現在ではジェネレータメソッドのGenerator.binomialの使用が推奨されています。
1. 書式
書き方:
Generator.binomial(n, p, size=None)
パラメーター:
| n: int or array_like of ints 試行回数(>= 0)。浮動小数点数を渡した場合は切り捨てで整数になる。 |
| p: float or array_like of floats 成功確率(0 <= p <= 1) |
| size: int or tuple of ints, optioal 出力する配列のshapeを指定。nとpが共にスカラーの場合は乱数を1つ返す。その他の場合は、np.broadcast(n, p).sizeの乱数を取得。 |
戻り値:
| out: ndarray or scalar 指定したパラメータのベータ分布から乱数を取得。それぞれの乱数は、n試行回数の上での成功数と等しい。 |
併せて確認したい関数
scipy.stats.binom: 確率密度関数、分布、累積密度関数など
Notes
二項分布の確率密度関数は次の式で表すことができます。
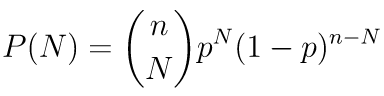
nは試行回数、pは成功確率、Nは成功回数です。
無作為標本を使って、人口における標準誤差の割合を見積もる時は、p*n<=5 でなければ、正規分布がうまく機能します。それ以外の場合は、二項分布がうまく機能します。p は人口割合の見積もりで、nは標本の数です。たとえば4名が左利き、11名が右利きの15名の標本の場合、p=4/15=27%です。そして0.27*15=4です。こうしたケースでは、二項分布を使うべきです。
2. サンプルコード
まずは、random.default_rng コンストラクタでジェネレータオブジェクトを作成します。『numpy.random.default_rng – 乱数生成のためのジェネレータオブジェクトの作成』に目を通しておいてください。
import numpy as np
rng = np.random.default_rng()
# >>> ジェネレータオブジェクト rng を作成
rng
こうして作成したジェネレータオブジェクト rng に対して、Generator.binomial を呼び出します。その際、第一引数に試行回数n、第二引数に確率p、第三引数にsizeを渡します。
例えば、以下のコードでは、成功確率10%の事象を20回試行します。それを5セット行った時に、それぞれのセット毎に成功が何回現れるかが示されています。
rng.binomial(20, .1, 5)
size は 2次元配列以上を指定することもできます。その際は、shapeをタプルで渡します。
rng.binomial(20, .1, (5, 2))
グラフにすると、ある確率の現象を、ある試行回数行った時に、その現象が実際にどのぐらい発生するかを一目で確認することができます。
import matplotlib.pyplot as plt
plt.subplot(121)
s = rng.binomial(15, .25, 10000)
count, bins, ignored = plt.hist(s, 30, density=True)
plt.title('n=15., p=.25', fontsize=12)
plt.subplot(122)
s = rng.binomial(100., .02, 10000)
count, bins, ignored = plt.hist(s, 30, density=True)
plt.title('n=100, b=.02', fontsize=12)
plt.tight_layout()
plt.show()
3. まとめ
以上。Generator.binomialは二項分布から乱数配列を生成するジェネレータメソッドです。
これまで使われていたnp.random.binomial 関数は継続して使用可能ですが、Generator.binomialメソッドを使った方が遥かに高速で科学技術計算に適しています。

コメント