np.sort関数は、NumPyの配列の要素をソートするために用意されている関数です。配列のソートはよく行う操作ですので、ここでわかりやすく解説したいと思います。
なお、NumPyには ndarray.sortメソッドも用意されています。これは使い方はnp.sort関数と同じです。しかし、np.sort関数は元の配列の要素をソートした新しい配列を作成しますが、ndarray.sortメソッドは元の配列そのものをソートするという違いがあります。
このページでは、np.sort関数をメインに解説していきますが、これを理解すれば、同時にndarray.sortメソッドもよく理解できます。
それでは始めましょう。
NumPy配列のソート方法のまとめ
NumPyの配列をソートする上で知っておきたい5つの関数については『NumPyのソート(並び替え)のために知っておきたい5つの方法』でまとめて簡潔に解説しています。ぜひそちらもご確認ください。
1. 書式
まずは書き方を確認しましょう。
書き方:
np.sort(a, axis=-1, kind='quicksort', order=None)
パラメーター:
| 引数 | 型 | 解説 |
| a | array_like | 配列を渡します。 |
| axis(optional) | int または None | どの軸方向に沿ってソートするかを指定します。デフォルト値は-1(最後の軸)です。Noneを指定した場合は1次元化した配列が使われます。 |
| kind(optional) | ‘quicksort’, ‘mergesort’, ‘heapsort’, ‘stable’ | どのソートアルゴリズムを使うかを指定します。 |
| order(optional) | str または list of str | 複数のデータ型を持つ構造化配列の場合、どのデータを基準にソートするかを指定します。 |
| ※ optional はオプション引数であることを示します。 | ||
戻り値:
| ndarray: 要素を指定の軸方向にソートした新しい配列 |
一緒に確認したい関数:
書き方:
ndarray.sort(axis=-1, kind='quicksort', order=None)
冒頭でも書きましたが、np.sort関数とndarray.sortメソッドは、オプション引数の使い方はまったく同じです。そのため、このページではnp.sort関数をメインに解説していきます。
ただし、np.sort関数は元の配列をソートした新しい配列を作成しますが、ndarray.sortメソッドは元の配列そのものをソートするという違いがありますので、この点はしっかり使い分けられるように覚えておきましょう。
Note
以下は、np.sort関数の中級者以上向けの解説です。ここは飛ばして、「2. サンプルコード」に移って頂いても全く問題ありません。
メモリスペースについて
最後の軸(axis=-1)以外のソートでは、この関数はデータの一時的なコピーを作成した上で、要素の並べ替えを行います。そのため、axis=-1 のソートは、他の次元軸に沿ったソートよりも早く、必要なメモリスペースも少なくなります。
複素数 nan値 nat値の並べ替えについて
複素数(complex型)の数値の並べ替え順は、辞書式の順序になります。つまり、基本的には実数部分によって並べ替えますが、実数部分が同値の場合は虚数部分によって並べ替えます。
配列にnan値がある場合は、nan は最後になります。Rを実数としたら、次のような順序になります。
Real: [R, nan]
Complex: [R+Rj, R+nanj, nan+Rj, nan+nan]
なお、NaT は NaN よりもさらに後ろに並べ替えられます。
ソートアルゴリズムについて
使用するソートアルゴリズムは、基本的にはデフォルトの ‘quicksort’ が高速です。
np.sort関数では、ソートアルゴリズムを選択することができますが、それぞれ平均速度・ワーストケースでのパフォーマンス・ワークスペースのサイズ・そして安定ソートかどうかが異なります。安定ソートとは、同値の値が複数ある時、ソート前と後でも位置関係を保持することを言います。
それぞれの違いを以下に載せておきます。
| 速度 | ワーストケース | メモリ領域サイズ | 安定ソート | |
|---|---|---|---|---|
| ‘quicksort’ | 1 | O(n^2) | 0 | no |
| ‘heapsort’ | 3 | O(n*log(n)) | 0 | no |
| ‘mergesort’ | 2 | O(n*log(n)) | ~n/2 | yes |
| ‘timsort’ | 2 | O(n*log(n)) | ~n/2 | yes |
デフォルトの’quicksort’ はイントロソートです。これはクイックソートによる並べ替えがうまく進まなかった場合は、ヒープソートに切り替わるというものです。つまり最悪のケースでもO(n*log(n))になるということです。基本的には、デフォルトのままが高速です。
オプション引数で ‘mergesort’ を指定したとしても、配列のデータ型に応じて ‘mergesort’ と ‘timsort’ のどちらかが自動選択されます。
オプション引数で ‘stable’を指定すると、データ型に応じて、Timソートと基礎ソートのうち最適な安定ソートアルゴリズムを選択します。Timソートは、ver1.17以降に追加されたもので、既にソートされたデータや、ほぼソートされたデータに対して高性能です。ランダムなデータに対しては、マージソートとほとんど同じ性能です。データ型が整数(int型)の配列の場合、’mergesort’と’stable’を指定すると基礎ソートになります。基礎ソートは、O(n log n) ではなく O(n) です。
2. サンプルコード
それではサンプルコードを見ながら使い方を確認していきましょう。
1次元配列のソート
1次元配列のソートはとてもわかりやすいです。
# 1次元配列を作成
import numpy as np
rng = np.random.default_rng()
x = rng.integers(0, 10, (5, ))
x
# ソート
np.sort(x)
多次元配列のソート
多次元配列の場合、デフォルトでは、次元数に関わらず、「最後の次元軸」、つまり横方向にソートします。
次元軸について簡単におさらいしておきましょう。2次元配列と3次元配列を例にすると、それぞれ下図のように次元軸が存在します。
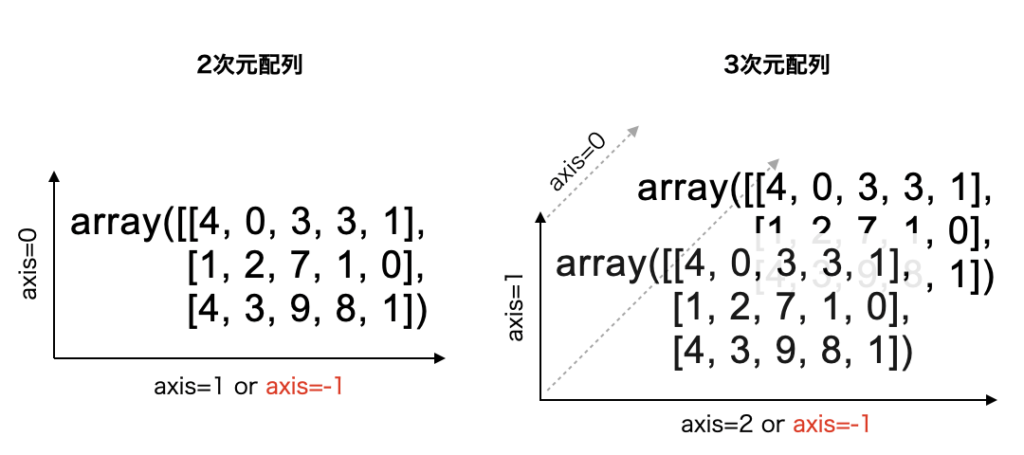
最も大きな次元軸を axis=0 として、番号がふられていきます。以下の画像を見るとわかりやすいでしょう。

このように配列をshape(m, n, k)で表した時の、最も左側の要素を「最初の軸」、最も右側の要素を「最後の軸」といいます。そのため、どれだけ次元数が増えたとしても「最後の軸」とは常に横方向の軸のことです。
しかし最初の軸 axis=0 がどの軸のことを指すかは、配列の次元数が増えるごとに変わります。
以上のことからnp.sort関数はデフォルトでは、対象とする配列の次元数に関わらず、常に横方向に並べ替えます。
以下は2次元配列の場合です。
# 2次元配列を作成
rng = np.random.default_rng()
x = rng.integers(0, 10, (3, 5))
x
# デフォルトでは横方向にソート
np.sort(x)
軸を指定してソート
オプション引数 axis= を指定すると、任意の次元軸でソートすることができます。
2次元配列の場合、axis=0 で縦方向にソートします。上の配列 x を縦方向にソートしてみましょう。
# 縦方向にソート
np.sort(x, axis=0)
なお3次元配列の場合は、axis=0 で奥行き方向にソートし、axis=1 で縦方向にソートします。先ほどの画像を見ると、すぐに理解できると思います。
ソートアルゴリズムの指定
オプション引数の kind= では、ソートアルゴリズムを変更することができます。これに関しては、正確に理解しなければいけないというものではありません。
結論から言うと、ほとんどの場合はデフォルトのクイックソートが最も速く、たまに他のアルゴリズムが速い場合があるというぐらいです。デフォルトでは処理速度が遅いなと感じたら、他のアルゴリズムを試してみるというようにすると良いでしょう。
それぞれ簡潔に解説しておきます。
クイックソートは、ランダムなデータをソートする際には、通常、最も高速なソートアルゴリズムです。
クイックソートでは、まず、ランダムに適当な数(ピボット)を選びます。そして、ピボットより小さい数を前に、大きな数を後ろに移動させます。そして、そうやって2分割したデータを、それぞれソートします。
以下のアニメーションがクイックソートです。
マージソートは、追加のワークスペース(記憶作業領域)が必要ですが、クイックソートと比べると最悪計算量が少なく、安定ソートのアルゴリズムです。しかし、ランダムなデータをソートする際は、通常クイックソートの方が速いです。
マージソートでは、まずデータを分割し、分割したデータをソートし、別のデータと併合し、またソートするということを繰り返します。
以下のアニメーションがマージソートです。

By Swfung8
ヒープソートは、元のデータの並びがどのようなものであっても、計算量の変化が小さいソートアルゴリズムです。しかし平均的にはクイックソートよりも遅いです。
ヒープソートは、最初に二分ヒープ木を作り、最大値か最小値を取り出し、ソートリストに追加していくアルゴリズムです。
以下のアニメーションがヒープソートです。
オプション引数 kind= では、これらのソートアルゴリズムのうちどれかを指定することができます。デフォルトは’quicksort’です。
# ソートアルゴリズムの指定
np.sort(x, kind='mergesort')
構造化配列のソート
対象となる配列が構造化配列(異なるデータ型をもつ配列)の場合は、オプション引数 order= で、どのデータを基準にソートするかを指定することができます。なお、構造化配列については『NumPyのdtype属性の一覧と参照・指定・変更方法』で解説しています。
まず、構造化配列を作成します。
import numpy as np
dtype = [('player', 'S6'), ('score', float), ('age', int)]
values = [('Taro', 95.8, 21), ('Jiro', 102.1, 19), ('Saburo', 83.5, 19)]
arr = np.array(values, dtype=dtype)
arr
この構造化配列を、scoreを基準にソートした場合と ageを基準にソートした場合を以下のコードで示しています。
# scoreを基準としてソートした
score = np.sort(arr, order='score')
print('score: \n', score)
# ageを基準としてソート
age = np.sort(arr, order='age')
print('age: \n', age)
それぞれ、指定のデータを基準にソートされています。
なお、このデータではageが同じ19のplayerが2人存在します。ここからさらに以下のように書くと、まずageでソートし、ageが同一の場合はscoreでソートすることができます。
''' ageでソートし同年齢の場合はscoreでソート '''
age_score = np.sort(arr, order=['age', 'score'])
print(age_score)
3. まとめ
以上がnp.sort関数の使い方です。配列のソートはよく行う操作の一つですので、しっかりと使いこなせるようにしましょう。



コメント