Python の NumPy 配列の数値演算ができるようになると、非常に高度な計算ができるようになります。ここでは、
- 配列の基本的な四則演算
- 配列の合計値・最大値・最小値・平均値
- 配列の標準偏差と偏差値
- 配列のベクトル演算
を例に解説していきます。これを見ると、配列が科学技術計算に不可欠であることも、何となく感じて頂けると思います。それでは見ていきましょう。
1. 配列の演算
配列の四則演算は、一つの配列に対する演算と、複数の配列同士の演算で扱いが異なります。それぞれ確認しましょう。
Python の演算の基本については「Pythonの演算子の一覧表とわかりやすい解説」で解説しているので、改めて確認してみると良いでしょう。
1.1. 四則演算
1.1.1. 一つの配列の四則演算
Python (NumPy) では配列の要素が数値の時は、四則演算を簡単に行うことができます。次の二次元配列を例に見ていきましょう。
import numpy as np
array = np.array([[1, 2], [3, 4]])
print(array)
配列に対して四則演算を行うと、全ての要素に対して、演算が反映されます。
'''配列に 1 を足すと、全ての要素の値に加算されます。'''
array1 = array + 1
print(array1)
引き算、掛け算、割り算も同様です。
print(array1 - 1) #引き算
print(array1 * 2) #掛け算
print(array1/2) #割り算
1.1.2. 配列同士の四則演算
配列同士の四則演算は、対応する位置にある要素同士で計算されます。次のコードをご覧ください。
import numpy as np
array1 = np.array([[1, 2], [3, 4]])
array2 = np.array([[10, 20], [30, 40]])
array3 = array1 + array2
print(array3)
このように、それぞれ次のように対応する位置にある要素の値同士で足し算が行われています。
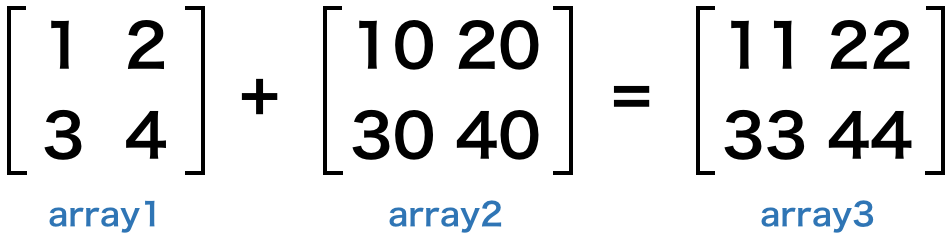
掛け算や割り算も同様です。
array4 = array1 * array2 #掛け算
print(array4)
array5 = array1 / array2 #割り算
print(array5)
1.1.3. 行と列の数が異なる配列同士の四則演算(ブロードキャスト)
行と列の数が異なる配列同士の演算では、足りない行と列の値が自動的に補われます。これをブロードキャストといいます。
例えば、次のコードをご覧ください。
import numpy as np
array1 = np.array([[1, 2], [3, 4]])
array2 = np.array([10, 20])
array3 = array1 + array2
print(array3)
このように、array2 の足りない行に、そのまま要素の値がスライドされて、演算が行われます。下図をご覧頂くと分かりやすいでしょう。
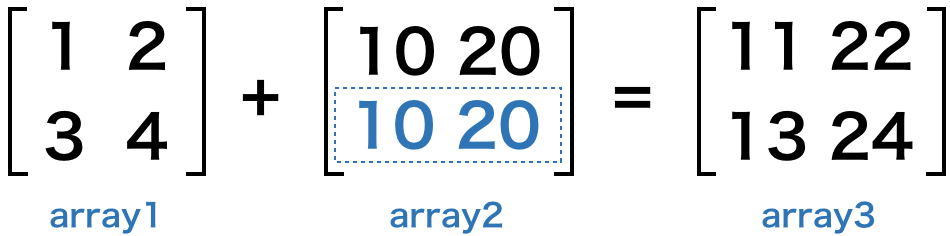
続いて、次の例を見てみましょう。今度は、行ではなく、列が足りない場合の演算です。
array4 = np.array([[1, 2, 3],[4, 5, 6]])
array5 =np.array([[10], [20]])
array6 = array4 + array5
print(array6)
この場合は、次のようにブロードキャストされて、演算が処理されます。
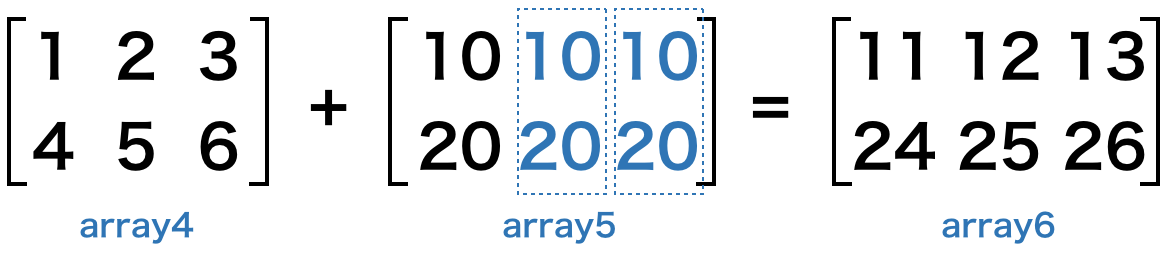
ただし、ブロードキャストは、演算を行う配列同士が、少なくとも行数か列数のどちらかが同一である必要がありますので、覚えておきましょう。
1.2. 配列の比較演算
次に比較演算について見てみましょう。
1.2.1. 単一の配列の比較演算
比較演算は、配列内の個々の要素に対して行われます。次のコードでは、配列に対して 5 より大きな数値が入っている値の位置を調べています。
import numpy as np
array = np.array([[6, 2, 9], [1, 2, 8]])
array > 5
次のコードは、9 と一致する値があるかどうかを調べています。
array == 9 # 9 と一致する値の位置を調べる。
1.2.2. 配列同士の比較演算
配列同士の比較演算も、行と列の各要素同士の比較になります。以下をご覧ください。次の例をご覧ください。
import numpy as np
a = np.array([1, 2, 3, 4, 5, 6]).reshape(2, 3)
b = np.array([1, 4, 2, 5, 3, 6]).reshape(2, 3)
c = (a == b)
print(c)
なお、Python では論理値の True は 1 、 False は 0 として処理されるので、その特性を利用して sum() メソッドで True の数を調べることができます。
'''True=1, False=0 のため、math() メソッドでTrueの数を調べることができます。'''
c.sum()
2. 配列の合計・最大値・最小値・平均値を求める
配列から、合計値、最大値、最小値、平均値も簡単に求めることができます。以下の二次元配列を使って、それぞれの値を求めていきましょう。
import numpy as np
array = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(array)
2.1. 配列の合計値を求める
合計値は sum() メソッドで調べることができます。
print(array.sum()) #全ての行と列の合計。
print(array.sum(0)) #引数に 0 を渡せば各列の合計。
print(array.sum(1)) #引数に 1 を渡せば各行の合計。
2.2. 配列の最大値を求める
最大値は max() メソッドで調べることができます。
print(array.max()) #最大値
print(array.max(0)) #引数に 0 を渡せば各列の最大値
print(array.max(1)) #引数に 1 を渡せば各行の最大値
2.3. 配列の最小値を求める
最小値は min() メソッドで調べることができます。
print(array.min()) #最小値
print(array.min(0)) #引数に 0 を渡せば各列の最小値
print(array.min(1)) #引数に 1 を渡せば各行の最小値
2.4. 配列の平均値を求める
平均値は mean() メソッドで調べることができます。
'''配列の中の平均値は mean() メソッドで調べます。'''
print(array.mean()) #平均値
print(array.mean(0)) #引数に 0 を渡せば各列の平均値
print(array.mean(1)) #引数に 1 を渡せば各行の平均値
2.5. numpy ライブラリの同名の関数を使う
ここまでは、numpy.ndarray 型オブジェクトのメソッドでしたが、numpy ライブラリにも同盟の関数があります。関数ですので、引数で、対象の配列を渡します(参照:「Pythonの関数の基礎知識と使い方と一覧まとめ」)。
以下をご覧ください。
'''numpy ライブラリの同名の関数を使うこともできます。'''
print(np.sum(array)) # sum() 関数
print(np.max(array,1)) # max()関数。第二引数に 1 を渡せば各行の最大値。
print(np.min(array, 0)) # min() 関数。第二引数に 0 を渡せば各列の最小値。
print(np.mean(array)) # mean() 関数
3. 配列の標準偏差を求める
配列の要素の標準偏差も、numpy ライブラリの std() 関数を使って求めることができます。そして、標準偏差を求められると、偏差値も計算することができます。
ここでは例として、ある学校のテストの標準偏差と偏差値を求めてみましょう。
偏差値を求めるには、平均値、偏差、分散が必要になります。この辺りに興味がある方は、統計学の標準偏差等について学んでみるといいでしょう。
それでは、次のコードをご覧ください。
import numpy as np
from random import randint
'''分散を 3.5、 平均を 65 点とします。'''
data = 3.5 * np.random.randn(200) + 65 #真ん中の関数は正規分布の乱数を作ります。
x = randint(50, 101) #自分の点数を 50 ~ 100 の乱数の中から作ります。
score = 10 * (x - data.mean())/data.std() + 50 # std()メソッドは標準偏差を求めるものです。
'''それぞれ出力します。'''
print("自分の点:", x)
print("平均点:", round(data.mean()))
print("標準偏差:", round(data.std()))
print("偏差値:", round(score))
コードの中に出てくる np.random.randn() は、numpy ライブラリの、正規分布をランダムに作成する関数です。この関数の戻り値は、配列(numpy.ndarray 型オブジェクト)です。
randint() 関数は、random モジュールの指定の数値の範囲の乱数を作成する関数です(参照:「Pythonのモジュールについて抑えておくべき知識とよく使うもの一覧」)。
4. 配列のベクトル演算
配列を利用すると、ベクトルの演算も簡単にできるようになります。
4.1. ベクトルの長さを求める
例えば、下図の座標を持つ 2 つの点をつなぐベクトルがあるとします。
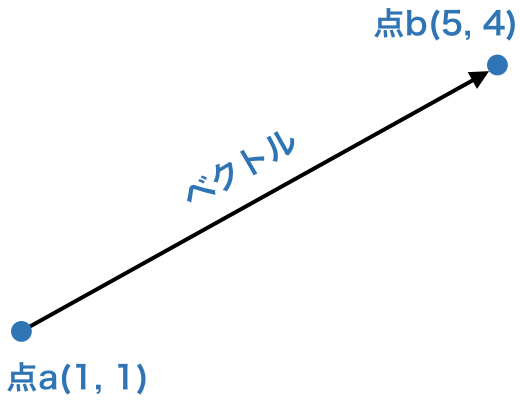
このベクトルの配列や、長さの演算を行うには、次のようなコードを書きます。なお、ベクトルの長さを求める関数は、numpy ライブラリの linalg.norm() 関数です。
import numpy as np
point_a = np.array((1, 1)) #点 a の座標
point_b = np.array((5, 4)) #点 b の座標
vector = point_b - point_a #点 b から 点 a へのベクトル計算
print(vector) #ベクトルを示し配列を出力します。
len_vector = np.linalg.norm(vector) #ベクトルの長さを求める関数です。
print(len_vector) #ベクトルの長さを出力します。
配列が、科学技術計算や機械学習に適していることを、何となく感じて頂ければと思います。上で計算したベクトルの長さの 2 倍のものが欲しい時は、掛け算を行えば求めることができます。
print(vector*2) #vectorを2倍にした配列を示す。
print(np.linalg.norm(vector*2)) #vector長さも2倍になります。
4.2. ベクトルの足し算と引き算
次にベクトルの足し算と引き算を見ていきましょう。
4.2.1. ベクトルの足し算
まずは、ベクトルの足し算を見てみましょう。下図をご覧ください。
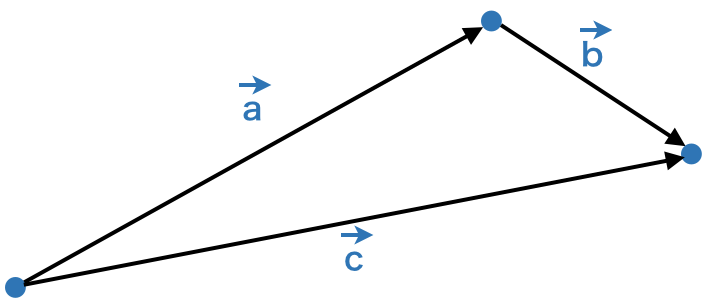
この場合、「ベクトル a + ベクトル b = ベクトル c」になります。この演算を行うコードが以下です(ベクトルの配列は適当に設定しています)。
import numpy as np
vector_a = np.array([4, 3]) #ベクトルa を示す配列
vector_b = np.array([3, -2]) #ベクトルb を示す配列
vector_c = vector_a + vector_b #ベクトルcを示す配列を求めます。
print(vector_c) #ベクトルcを示す配列
print(np.linalg.norm(vector_c)) #ベクトルcの長さ
4.2.2. ベクトルの引き算
次にベクトルの引き算を見てみましょう。下図をご覧ください。
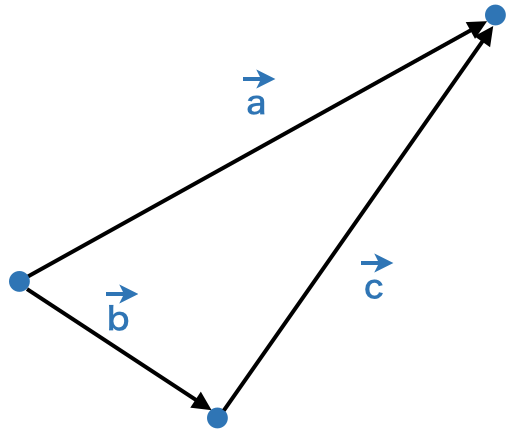
この場合、「ベクトル a – ベクトル b = ベクトル c」になります。この演算を行ってみましょう。ベクトル a と ベクトル b の向きと長さは上で用いたものと同じです。
vector_c = vector_a - vector_b #ベクトルcを示す配列を求めます。
print(vector_c) #ベクトルcを示す配列
print(np.linalg.norm(vector_c)) #ベクトルcの長さ
4.3. 内積と外積の演算
配列を使うと、高校数学であるようなベクトルの計算で便利な内積や外積も、簡単に行えるようになります。見てみましょう。
4.3.1. 内積の演算
配列を使うと、行と列の内積を、numpy ライブラリの dot() 関数で行うことができます。下図は、2 × 2 の行列同士の内積です。
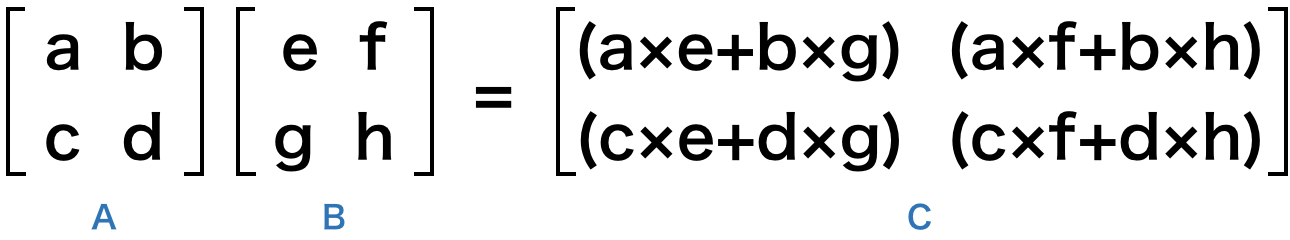
これをコードで書くと、次のようになります。
import numpy as np
a = np.array([[1, 2],[3, 4]])
b = np.array([[5, 6],[7, 8]])
c = np.dot(a, b) #dot()関数で内積を求めます。
print(c)
それでは、この内積の演算を用いて、以下のように、ある物体を動かした時の仕事を計算して見ましょう。
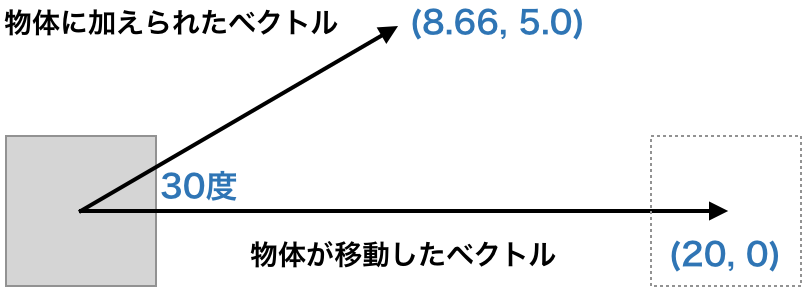
次のコードをご覧ください。
force = np.array([8.66, 5.0]) #物体に加えた力
moved_vector = np.array([20, 0]) #力を受けて物体が動いた量
work = np.dot(force, moved_vector) #仕事量
print(work)
これを、ベクトルとコサインから計算すると、次のようなコードになります。
f = np.linalg.norm(force) #物体に加えたベクトルの長さ
m = np.linalg.norm(moved_vector) #物体が動いたベクトルの長さ
r = np.radians(30) #角度をラジアンに変換
w = f*m*np.cos(r) #仕事の計算
print(w)
内積から求めるととても楽ですね。
4.3.2. 外積の演算(三次元ベクトル)
三次元ベクトル(三次元配列)の外積は cross() 関数で求めることができます。例えば、下図のような三次元ベクトルの場合、 c は a と b の外積で求めることができます。
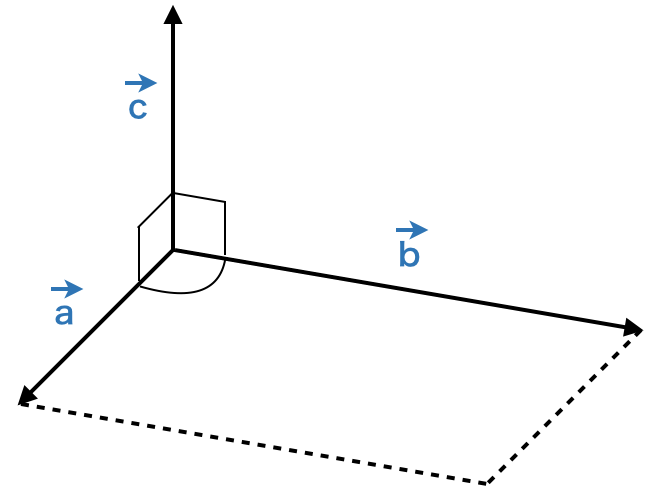
早速求めてみましょう。
import numpy as np
a = np.array([1, 2, 0]) #三次元配列は、[行, 列, 奥行き] で指定。
b = np.array([0, 1, -1])
c = np.cross(a, b) #ベクトルcを外積で計算。
print(c)
print(np.linalg.norm(c))
5. まとめ
一通り紹介してきましたが、Python で NumPy の配列を使うと、さらに様々な演算や数値計算ができるようになります。英語ですが、NumPy の公式サイトで確認することができます。数学計算のモジュールには、他に math モジュールが有名です。
math モジュールと NumPy ライブラリは同名の関数があります。
例えば、三角関数の sin() や cos() 関数ですね。しかし math モジュールの関数の場合は、引数には 1 つの値しか渡すことはできません。一方で NumPy ライブラリの関数の場合は、引数にリストや配列を渡して、複数の値のsinの値を一度に返すことができます。
こうした利点があるため、数値の複雑な分析を行う際には、NumPy の配列は必須と言えるでしょう。


コメント
コメント一覧 (1件)
いつも大変勉強させて頂いていおります。
全てのページを見て、学習させて頂きました。大変詳しくわかりやすい解説でした。是非引き続きブログ楽しみにしております。