行列とベクトルの積

行列とベクトルの積は、線形代数において基本的な行列の演算の一つです。当ページでは、これについて以下のことがわかります。

行列とベクトルの積とは何か

「行列とは」で述べた通り、ベクトルはデータであり、行列はベクトルを変換するための写像（関数）です。そして行列とベクトルの積は、関数である行列にデータであるベクトルを入力することによって、新しいベクトルを作るということを意味します。

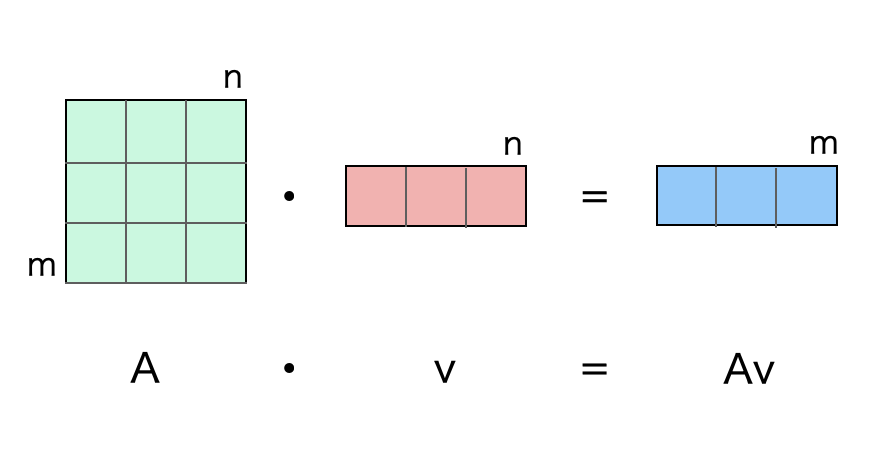
以上が行列とベクトルの積の割り算です。

行列とベクトルの積のやり方

行列とベクトルの積は、行列の列数とベクトルの要素数が同じである場合に行うことができます。これも行列のドット積と同じように \(\cdot\) 演算子を使って、 \(y=A \cdot v\) と表します。ベクトルは 1 つの列しか持たないので、計算結果は、要素数が行列の行数と同じベクトルになります。

\[y(m)=A(m,n) \cdot v(n)\]

以下の行列とベクトルがあるとします。

\[\begin{eqnarray}
A=
\begin{pmatrix}
a_{1,1}
&
a_{1,2}\\
a_{2,1}
&
a_{2,2}\\
a_{3,1}
&
a_{3,2}
\end{pmatrix}, \ \ \
v=
\begin{pmatrix}
v_1\\
v_2
\end{pmatrix}
\end{eqnarray}\]

これらの行列とベクトルの積は次のように求められます。

\[\begin{eqnarray}
y=
\begin{pmatrix}
a_{1,1} v_{1} + a_{1,2} v_{2}\\
a_{2,1} v_{1} + a_{2,2} v_{2}\\
a_{3,1} v_{1} + a_{3,2} v_{2}
\end{pmatrix}
\end{eqnarray}\]

例を見てみましょう。

\[\begin{eqnarray}
\begin{pmatrix}
1
&
2\\
3
&
4\\
5
&
6
\end{pmatrix}
\cdot
\begin{pmatrix}
3\\
2
\end{pmatrix}
&=&
\begin{pmatrix}
1 \times 3 + 2 \times 2\\
3 \times 3 + 4 \times 2\\
5 \times 3 + 6 \times 2
\end{pmatrix}\\
&=&
\begin{pmatrix}
7\\
17\\
27
\end{pmatrix}\
\end{eqnarray}\]

Pythonで行列とベクトルの積

Python では NumPy の配列に対して dot() メソッドを使うか @ 演算子でつなぐことで求めることができます。

# NumPy のインポート
import numpy as np

# 行列の定義
A = np.array([[1,2],[3,4],[5,6]])
print(A)

[[1 2]
 [3 4]
 [5 6]]

# ベクトルの定義
B = np.array([3,2])
print(B)

[3 2]

# 行列とベクトルの積
C = A.dot(B)
print(C)

[ 7 17 27]

# 行列とベクトルの積
C = A@B
print(C)

[ 7 17 27]