行列の掛け算(ドット積)は、線形代数において基本的な行列の演算の一つです。当ページでは、これについて以下のことがわかります。
このページでわかること
- 行列の掛け算(ドット積)とは何か
- 行列の掛け算(ドット積)のやり方
- Python で行列の掛け算(ドット積)
行列の掛け算(ドット積)とは何か
「行列とは」で述べた通り、行列はベクトルを変換するための写像(関数)です。そして行列のドット積は、何らかの目的で 2 つの関数で掛け算を行なって、シェイプの異なる新しい 3 つ目の関数を作るということを意味します。
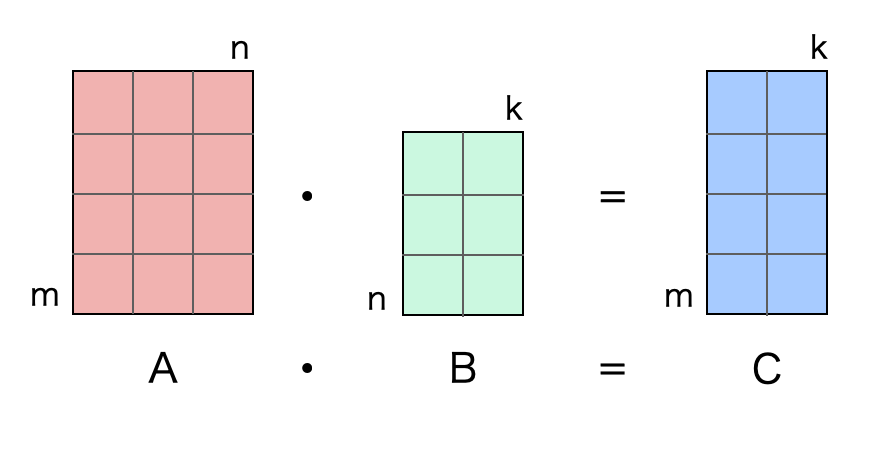
以上が行列のドット積です。
行列の掛け算(ドット積)のやり方
ドット積は、ここまで見てきた演算のように同じシェイプの行列同士であれば求められるというものではありません。ドット積を求めるには、2 つの行列 \(A\) と \(B\) が次のルールを満たしている必要があります。
- 1 つ目の行列 \(A\) の列の数 \(n\) が、2 つ目の行列 \(B\) の行の数 \(m\) と同じでなければならない。
たとえば行列 \(A\) のシェイプが \(m\) 行 \(n\) 列で、行列 \(B\) のシェイプが \(n\) 行 \(k\) 列だとします。この場合 \(A\) の列数と \(B\) の行数はお互いに \(n\) で同数なのでドット積を行うことが可能です。そしてドット積を行うと \(m\) 行 \(k\) 列の新しい 3 つ目の行列ができます。
\[C(m,k)=A(m,n) \cdot B(n,k)\]
例として、以下の 2 つの行列 \(A\) と \(B\) のドット積を求めてみましょう。
\[\begin{eqnarray}
A=
\begin{pmatrix}
a_{1,1}
&
a_{1,2}\\
a_{2,1}
&
a_{2,2}\\
a_{3,1}
&
a_{3,2}
\end{pmatrix}, \ \ \
B=
\begin{pmatrix}
b_{1,1}
&
b_{1,2}\\
b_{2,1}
&
b_{2,2}
\end{pmatrix}
\end{eqnarray}\]
これらの行列のドット積は次のように計算します。
\[\begin{eqnarray}
A \cdot B=
\begin{pmatrix}
a_{1,1} \times b_{1,1} + a_{1,2} \times b_{2,1}
&
a_{1,1} \times b_{1,2} + a_{1,2} \times b_{2,2}\\
a_{2,1} \times b_{1,1} + a_{2,2} \times b_{2,1}
&
a_{2,1} \times b_{1,2} + a_{2,2} \times b_{2,2}\\
a_{3,1} \times b_{1,1} + a_{3,2} \times b_{2,1}
&
a_{3,1} \times b_{1,2} + a_{3,2} \times b_{2,2}
\end{pmatrix}
\end{eqnarray}\]
例を見てみましょう。
\[\begin{eqnarray}
\begin{pmatrix}
1
&
2\\
3
&
4\\
5
&
6
\end{pmatrix}
\cdot
\begin{pmatrix}
7
&
8\\
9
&
10
\end{pmatrix}
&=&
\begin{pmatrix}
1 \times 7 + 2 \times 9
&
1 \times 8 + 2 \times 10\\
3 \times 7 + 4 \times 9
&
3 \times 8 + 4 \times 10\\
5 \times 7 + 6 \times 9
&
5 \times 8 + 6 \times 10
\end{pmatrix}\\
&=&
\begin{pmatrix}
25
&
28\\
57
&
64\\
77
&
100
\end{pmatrix}\
\end{eqnarray}\]
Pythonで行列の掛け算(ドット積)
Python では NumPy で作成した行列に対して、dot() メソッドを使うか、@ 演算子で繋ぐことでドット積を求めることができます。
# NumPy のインポート
import numpy as np
# 1 つ目の行列の定義
A = np.array([[1,2],[3,4],[5,6]])
print(A)
# 2 つ目の行列の定義
B = np.array([[1,2],[3,4]])
print(B)
# 行列のドット積
C = A.dot(B)
print(C)
# 行列のドット積
C = A@B
print(C)