ベクトルの掛け算（ドット積）

線形代数においてベクトルの掛け算（ドット積）は基本的な演算の一つです。このページではベクトルの掛け算（ドット積）について以下のことを解説します。

ベクトルの掛け算（ドット積）とは

「ベクトルとは」では、プログラマーにとってベクトルはデータであり数値のリストであるということを解説しました。物理学や数学ではベクトルは「長さと向きをもつ矢印」であると考えますが、データサイエンスにおいては単なるデータです。

これ以上でも以下でもありません。

そのため物理学や数学では、ベクトルのドット積は 2 つの矢印の一方を他方のベクトルに投影したときの射影の長さ（＝ベクトルの内積）を意味しますが、私たちプログラマーは基本的にそのように幾何学的に考えることはありません。

プログラマーにとってベクトルのドット積とは、「ベクトルの分解の際に使う目的やベクトルの直交性を確認する目的などで、同じサイズのベクトル（データ）同士で掛け算を行って、一つの値（スカラー）を得る手段」に過ぎないのです。

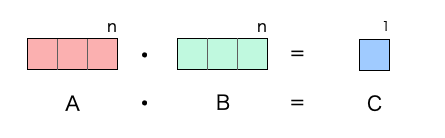
以上がプログラマーにとってのベクトルのドット積です。

ベクトルの掛け算（ドット積）のやり方

ベクトルのドット積は、足し算や引き算、アダマール積、割り算とは異なります。一番の違いは、ドット積は新しい別のベクトルを作るためのものではなく、一つのスカラー値を得るためのものです。具体的には次のように計算します。

2 つのベクトル \(a\) と \(b\) があるとします。

\[\begin{eqnarray}
a&=&
\begin{pmatrix}
a_1 & a_2 & a_3
\end{pmatrix}\\
b&=&
\begin{pmatrix}
b_1 & b_2 & b_3
\end{pmatrix}
\end{eqnarray}\]

このときドット積は次のように計算されます。

\[
a \cdot b =a_1 \times b_1 + a_2 \times b_2 + a_3 \times b_3
\]

例として、以下のベクトルのドット積を計算してみましょう。

\[\begin{eqnarray}
a&=&
\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}\\
b&=&
\begin{pmatrix}
4 & 5 & 6
\end{pmatrix}
\end{eqnarray}\]

次のようになります。

\[
a \cdot b =1 \times 4 + 2 \times 5 + 3 \times 6 = 32
\]

Pythonでベクトルの掛け算（ドット積）

Python では NumPy の配列に対して dot() メソッド、もしくは @ 演算子を使うことでドット積を求めることができます。@ 演算子を用いた方法は Python の ver 3.5. 以降に実装された比較的新しい機能です。

以下の 2 つのベクトルを使って確認してみましょう。

# NumPy のインポート
import numpy as np

# 1つ目のベクトルの定義
a = np.array([1, 2, 3])
print(a)

[1 2 3]

# 2つ目のベクトルの定義
b = np.array([1, 2, 3])
print(b)

[1 2 3]

まずは dot() メソッドを使った方法です。

# ベクトルのドット積（dot() メソッド）
c = a.dot(b)
print(c)

14

次に @ 演算子を使った方法です。

# ベクトルのドット積（@演算子）
d = a @ b
print(d)

14

一緒に読んでおきたいページ

• ベクトルの内積とは？誰でも理解できるようにわかりやすく解説