線形代数においてベクトルの掛け算(アダマール積)は、もう一つのドット積ほど使われるわけではありませんが、基本的な演算の一つです。このページではベクトルの掛け算について以下のことを解説します。
当ページでわかること
- ベクトルの掛け算(アダマール積)とは何か
- ベクトルの掛け算(アダマール積)のやり方
- Pythonでベクトルの掛け算(アダマール積)
ベクトルの掛け算(アダマール積)とは
「ベクトルとは」では、プログラマーにとってベクトルはデータであり数値のリストであるということを解説しました。物理学や数学ではベクトルは「長さと向きをもつ矢印」であると考えますが、データサイエンスにおいては単なるデータです。
これ以上でも以下でもありません。
そのため物理学や数学では、ベクトルの掛け算(アダマール積)は 2 つの矢印から新しい別の矢印を作るものですが、私たちプログラマーは基本的にそのように幾何学的に考えることはありません。
プログラマーにとってベクトルの掛け算(アダマール積)とは、「機械学習のためのデータの準備などの何らかの目的で、同じサイズのベクトル(データ)同士で掛け算を行って、同じサイズの新しいベクトル(データ)を作る手段」に過ぎないのです。
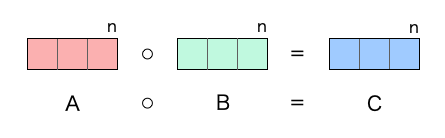
以上がプログラマーにとってのベクトルの掛け算(アダマール積)です。
ベクトルの掛け算(アダマール積)のやり方
ベクトルの掛け算は非常に簡単です。以下の 2 つのベクトル \(a\) と \(b\) を掛け算すると、それぞれ同じ場所の要素同士が掛け合わされます。
\[\begin{eqnarray}
a&=&
\begin{pmatrix}
a_1 & a_2 & a_3
\end{pmatrix}\\
b&=&
\begin{pmatrix}
b_1 & b_2 & b_3
\end{pmatrix}\\
a \circ b&=&
\begin{pmatrix}a_1 \times b_1 & a_2 \times b_2 & a_3 \times b_3\end{pmatrix}
\end{eqnarray}\]
たとえば、次のようになります。
\[\begin{eqnarray}
a&=&
\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}\\
b&=&
\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}\\
a \circ b&=&
\begin{pmatrix}
1 & 4 & 9
\end{pmatrix}
\end{eqnarray}\]
なおベクトルの引き算はお互いの要素の数が同じである場合のみ可能です。お互いのベクトルの要素の数が異なる場合は引き算はできません。
Pythonでベクトルの掛け算(アダマール積)
Python では NumPy で作成した配列同士を * 演算子で繋ぐことでベクトルの掛け算ができます。以下のコードをご覧ください。
# NumPy のインポート
import numpy as np
# 1つ目のベクトルの定義
a = np.array([1, 2, 3])
print(a)
# 2つ目のベクトルの定義
b = np.array([3, 2, 1])
print(b)
# ベクトルの掛け算
c = a * b
print(c)