ポアソン分布は、統計学において使われる代表的な離散確率分布の一つであり、「稀にしか起こらないような現象が、一定の期間内に何回起こることが期待できるかの確率の分布」です。ベイズ統計において、同じ離散確率分布の二項分布と並んで扱う機会が多い分布ですので、ここでしっかりと理解しておきましょう。
当ページでは、このポアソン分布について以下の内容を学ぶことができます。
当ページで学べること
- ポアソン分布がどういう時に使える分布なのかがわかる
- ポアソン分布の確率質量関数の計算方法とグラフの描き方がわかる
- ポアソン分布がどのように導出されているのかがわかる
- ポアソン分布の性質がわかる
- ポアソン分布の例題を実際に解くことで理解を深めることができる
なお、ポアソン分布の前に、まだ二項分布について知らない方は、先に『二項分布とは?誰でも必ず理解できるようにわかりやすく解説』をご覧ください。また確率分布そのものについては『確率分布とは?誰でも必ず理解できるようにわかりやすく解説』で解説しています。
それでは始めましょう。
1. ポアソン分布とは
ポアソン分布は、簡単に言うと、「滅多に起こらない出来事が任意の時間(面積や回数でも可)当たりに起こる回数」を表す確率分布です。訪問営業での成約数やゴルフのホールインワンの成功数など、起こる確率 \(\lambda\) がとても小さいものをイメージするとわかりやすいでしょう。
たとえば、ある営業マンの訪問営業の成約率が \(\lambda =3%\) だったとしたら、実際に 100 件を訪問したときの成約数の分布は以下の通りになります。
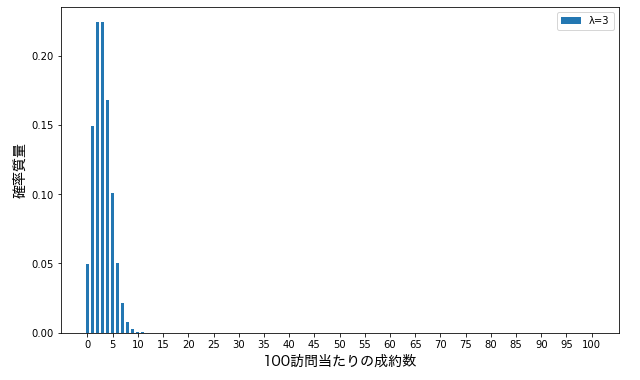
このように見てみると、制約数は最低 0 件から最大 10 件程度まで見込めることがわかります。
ポアソン分布は他にも、単位時間当たりの詐欺電話の数や、単位面積当たりのトルコ料理屋の数、単位回数当たりのホールインワン数など、様々な、稀にしか起こらない現象の起こる回数の確率を知るのに役立ちます。
2. ポアソン分布の計算(確率質量関数)
ポアソン分布の確率質量関数は以下の通りです。
ポアソン分布の確率質量関数
\[
P(k|\lambda) = \dfrac{\lambda^k}{k!}\cdot e^{-\lambda}
\]
\(\lambda\) : 任意の事象が任意の単位当たりに起こる割合
計算例として、定食屋の来客数を考えてみましょう。
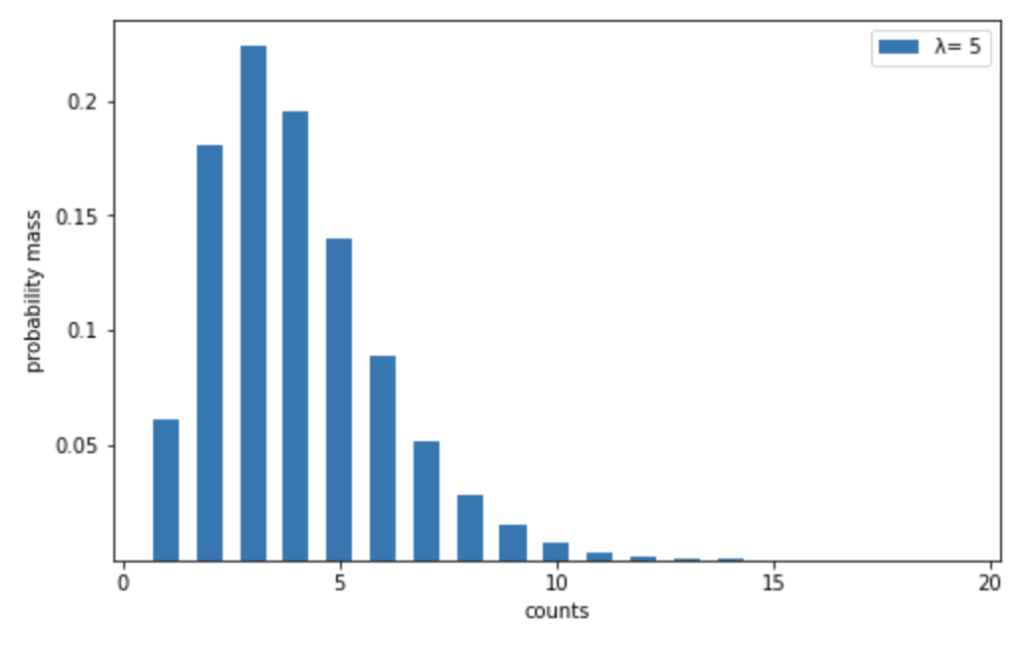
ある定食屋のランチタイムでは、平均して 12 分間に 1 組の来客があるとします。このとき、ランチタイムの、ある 60 分間における来客数の確率はどのようになるでしょうか。
これは \(\lambda=60 \div 12 = 5\) のポアソン分布モデルに従います。それでは、この場合 60 分間に来客が \(k=0\) 組になる確率はどれぐらいあるでしょうか。これは次のように計算でき、ほとんど 0 % に近いことがわかります。
\[\begin{eqnarray}
\dfrac{\lambda^k}{k!}\cdot e^{-\lambda}
=
\dfrac{5^0}{5!}\cdot e^{-5}
\approx
0.00005615
\end{eqnarray}\]
これを異なる確率変数の実現値 \(k\) : 来客数で計算したものが以下のコードです。
from scipy.stats import poisson
for i in range(0, 16):
print("k=",i," : " ,poisson.pmf(5,i))
それでは、この定食屋で 60 分間に 10 組以上15組以下の来客がある可能性はどれぐらいあるでしょうか。これは \(k=10\) 以上 \(15\) 以下の場合の確率質量を足し合わせれば良いので次のようになります。
\[\begin{eqnarray}
\sum_{k=10}^{n=15}
\approx
0.0224+0.0127+0.0070+0.0037+0.0019
\approx
0.0477
\end{eqnarray}\]
このように 5%弱という意外と大きい確率であることがわかります。このことから突然の来客者増も想定して、店のレギュレーションを考えておいた方が良さそうなことがわかります。
3. ポアソン分布の導出
繰り返しになりますが、ポアソン分布は「二項分布における成功率 \(p\) が非常に小さい場合に、試行回数 \(n\) が無限大になったとしたら、どうなるか?」を求めたものです。
- 二項分布:試行回数が \(n\) 、成功率が \(p\) である事象が \(k\) 回起こる確率の分布
- ポアソン分布:ある一定の期間内において、発生率が \(\lambda\) である事象が、\(k\) 回起こる確率の分布
どちらも事象が \(k\) 回起こる回数の確率分布ですが、二項分布では試行回数がわかっている一方で、ポアソン分布ではそれは明らかではないという違いがあります。なぜならポアソン分布は、試行回数が無限回であることを前提としているからです。
数式で確認していきましょう。
まず二項分布から見ていきたいと思います。たとえば、10000 分間(\(n=1000\) )で、1 組の来客がある場合、成功率は \(p=1 \div 10000 = 0.0001\) になります。そして、10000 分間での実際の来客数を確率変数を \(X\) とすると、\(n=10000\) で \(k\) 組が来店する可能性は、二項分布の以下の確率質量関数で求められます。
\[\begin{eqnarray}
P(X=k)
=
\dbinom{10000}{k}(0.0001)^k(1-0.0001)^{10000-k}
=
{}_{10000}C_k(0.0001)^k(0.9999)^{10-k}
\end{eqnarray}\]
さて、このように成功率が極端に低い場合、試行回数 \(n\) が多少変わったとしても、二項分布の期待値 \(np\) の値はほとんど変わりません。そこで、期待値 \(np\) は定数であることにして \(np=\lambda\) と表記を、一つの記号に置き換えることにします。
このように期待値が定数 \(\lambda\) の場合で、試行回数を極限(無限回)に増やしてみたらどうなるかを求めたものがポアソン分布です。以下の通りです。
\[\begin{eqnarray}
\lim_{\lambda=nk, n \rightarrow \infty}
\dbinom{n}{k}
p^k(1-p)^{n-k}
=
\dfrac
{\lambda^k }{k!} \cdot e^{-\lambda}
\end{eqnarray}\]
なお、途中の計算式は複雑なので省略しています。ポアソン分布 – Wikipedia で記載がありますので、興味がある方はそちらをご覧ください。
つまり、ポアソン分布は二項分布の極限なのです。以上がポアソン分布の導出です。
要は、二項分布において、期待値が定数であるとして、試行回数を極限にまで増やした場合が、ポアソン分布だということです。
4. ポアソン分布の期待値(平均)と分散
ポアソン分布の最大の特徴は、期待値(平均)と分散が \(\lambda\) になることです。
\[
{\small 期待値} = {\small 分散} = {\lambda}
\]
これは考えてみれば当たり前のことです。\(\lambda\) は事象の発生率(=ある一定期間における事象の発生回数)なのですから、当然これは期待値と一致します。
そしてポアソン分布は、期待値を頂点とした正規分布のようなものなので、分散は必ず期待値と同じになります。これについては、分散の計算式 \(\dfrac{1}{n} \sum_{i=1}^n (x_i – {\small 期待値})^2\) をイメージすると理解できるようになります。
また、すぐ上の「ポアソン分布の導出」を見ると、より理解できるようになります(考えるためのヒントが全て揃う)ので、ぜひ一度はご確認ください。
5. ポアソン分布の例題
それでは例題として、以下の問題にチャレンジしてみてください。
5.1. 9 年あたりの死亡事故の発生数
問題
ある交差点では、過去 9 年間で 3 件の死亡事故が発生しました。これについて、ポアソン分布を用いて、以下の 2 つの問いに答えなさい。
あ
- (1) 今後 9 年で死亡事故が 2 件以下に減る確率
- (2) 今後 9 年で死亡事故が 3 件以上 15 件以下発生する確率
まず、問題は 9 年間における発生率を聞いており、データも過去 9 年間のものなので、このポアソン分布のラムダは \(\lambda=3\) になります。そして、この条件で確率質量関数を計算し、それをグラフに描いたものが以下です。
from scipy.stats import poisson
for i in range(1, 16):
print("k=",i," : " ,poisson.pmf(3,i))
以上のことから解答はそれぞれ次の通りになります。
(1) 今後 9 年で死亡事故が 2 件以下に減る確率
\[\begin{eqnarray}
\sum_{k=1}^{n=2}
\dfrac{\lambda^k}{k!}\cdot e^{-\lambda}
\approx
0.061+0.180
\approx
0.241
\end{eqnarray}\]
(2) 今後 9 年で死亡事故が 3 件以上 15 件以下発生する確率
\[\begin{eqnarray}
\sum_{K=3}^{n=15}
\dfrac{\lambda^k}{k!}\cdot e^{-\lambda}
\approx
0.759
\end{eqnarray}\]
以上のことから、このままでは今後 10 年で、また死亡事故が複数発生することがわかります。早急に交差点を整備すべきでしょう。
5.2. 3 年あたりの死亡事故の発生数
問題
上と同じ問題で以下の確率について答えなさい。
- 今後 3 年で死亡事故が 1 件以上 3 件以下発生する確率
まず、問題は 3 年間における発生率を聞いており、データは過去 9 年間のものなので、このポアソン分布のラムダは \(\lambda=3 \div 3\=1\) になります。そして、この条件で確率質量関数を計算し、それをグラフに描いたものが以下です。
from scipy.stats import poisson
for i in range(1, 16):
print("k=",i," : " ,poisson.pmf(1,i))
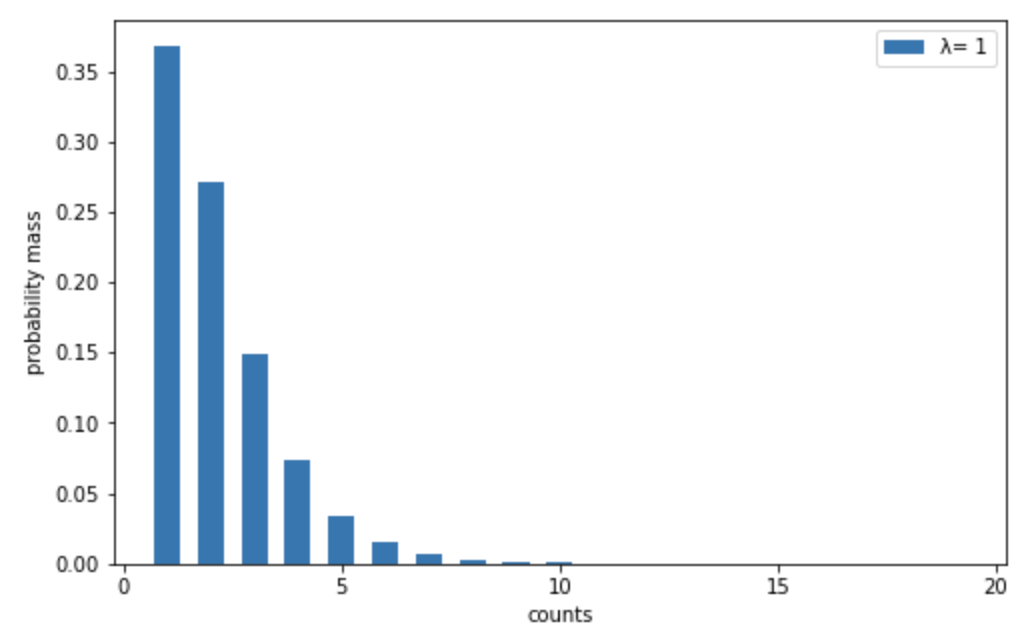
以上のことから答えは以下の通りになります。
\[\begin{eqnarray}
\sum_{k=1}^{n=3}
\dfrac{\lambda^k}{k!}\cdot e^{-\lambda}
\approx
0.368+0.271+0.149
\approx
0.788
\end{eqnarray}\]
6. まとめ
最後に重要ポイントをまとめておきます。
ポアソン分布とは
統計学において使われる代表的な離散確率分布の一つであり、「稀にしか起こらないような現象が起こる確率」の分布のことです。確率質量関数は以下の通りです。
\[
P(X=k) = \dfrac{\lambda^k}{k!}\cdot e^{-\lambda}
\]
\(P(X=k)\):所与の時間内に平均 \(\lambda\) 回発生する事象が \(k\) 回発生する確率、\(\lambda\):事象の発生率
\(k\)(確率変数):事象の発生回数
ポアソン分布の期待値と分散
ポアソン分布の特徴はなんといっても、期待値と分散が同じ値になるところにあります。
\[
{\small 期待値} = {\small 分散} = {\lambda}
\]
以上、最後までご覧頂きありがとうございました。
当ページが、あなたにとって学習の役に立ったとしたら、幸いです。もし、役に立ったと感じたら、SNS 上でシェアして頂ければ嬉しく思います。また、コメントも頂けるとモチベーションが上がります(コメント返信は余裕ができれば行いたいと考えています)。

コメント
コメント一覧 (2件)
(1) 今後 9 年で死亡事故が 2 件以下に減る確率でk=0はないのでしょうか?
この定食屋で 60 分間に 10 組以上15組以下の来客がある可能性は10組の確率(k= 10 : 0.03783327480207079)も足しこんで、おおよそ8.5%程度ではないでしょうか?