MENU
  1. ホーム
  2. AI数学
  3. ベイズ統計
  4. 尤度の意味と計算方法をわかりやすく解説

尤度の意味と計算方法をわかりやすく解説

ベイズ統計
2021年8月24日

尤度（読み方「ゆうど」 英語 “likelihood”）は、機械学習で必ず出てきますし、近年になって一躍脚光を浴びているベイズ統計を理解する上でも必須の概念でもあります。しかし尤度の解説は、複雑なものばかりで、なかなか直感的に理解することはできません。

そこで当ページでは、数式は非常に簡単なもののみに留め、誰でも尤度を理解できるように解説していきます。尤度の意味だけを知りたい場合は、数学がわからなくても理解できますので、ぜひご覧ください。

なお、数式は簡単なもののみと言っても、確率とベイズの定理の基本知識は理解しておく必要があります。それぞれ以下のページで解説していますので、不安がある場合は、先に確認しておいてください。

それでは尤度の解説を始めます。

目次

1. 尤度とはわかりやすく

尤度とは、わかりやすく言うと「ある結果から、どのような前提条件があったと推測するのが妥当なのかを教えてくれる指標」です。

これは以下に記しているベイズの定理の計算項目の 1 つです。

ベイズの定理

\[\begin{eqnarray}
\overbrace{P(A|B)}^{事後確率}
=
\dfrac
{
\overbrace{P(B|A)}^{尤度}
\overbrace{P(A)}^{事前確率}
}
{
P(B)
}
\end{eqnarray}\]

このベイズの定理において、「事後確率 P(A|B)」 は、〈 B という前提条件の下で A という結果が起こる確率〉を意味します。

これに対して「尤度 P(B|A)」 は、〈 A という結果から、前提条件が B であったと推測することの尤もっともらしさ（妥当性）を表す値〉を意味します。尤度も確率と同じように 0 ~ 1 の範囲の値を取ります。

尤度と確率の違い

  • P(A|B) 事後確率：B という前提条件の下で、A という結果が起こる確率
  • P(B|A) 尤度：A という結果から、前提条件が B であったと推測することの妥当性

わかりやすく説明しましょう。

たとえば、箱の中に白石と黒石が合計 30 個入っていたとします。白石と黒石の比率はわかりません。そして、この箱から 5 個の石を取り出したら、内訳は白石が 4 個・黒石が 1 個だったとします。

このような結果が出た場合、この箱にはもともと白石は 4 個（＝黒石は 26 個）入っていたと推測することの尤度は最小の 0.0018% になります。一方で、白石は 24 個（＝黒石は 6 個）入っていたと推測することの尤度は最大の 44.74 % になります。

つまり、いま現在のデータから、箱の中にはもともと 24 個の白石と 6 個の黒石が入っていたという推測が最大尤度となるため、もっともあり得る前提条件だと判断できるのです。

このように尤度は、ある結果を観察して、その結果から、どのような前提条件があったと推測するのが妥当なのかを教えてくれる指標です。

現実世界で、私たちは、判断に必要な情報を全て集められることは絶対にありません。つまり、いつだって不十分な情報の中から重大な決断を下さなければいけないのです。そうした現実において、現在わかっている情報から、尤もあり得る前提条件を数学的に推測するという技術にはとても大きな意味があります。それによって、少しでも良い判断を下せる可能性が高まるからです。

以上のことから尤度は非常に重要な概念であるということに同意しない人はいないでしょう。

2. 尤度の求め方

それでは尤度の算出方法を見ていきましょう。以下の問題をご覧ください。

問題

箱の中に白と黒の石が 30 個入っています。白と黒の比率は分かりません。この箱から石を 5 個とりだしたところ、白が 4 個、黒が 1 個でした。この結果から、次に取り出す石が白である確率を求めるといくつになるでしょうか。

これは上で解説したものと同じものですが、このような問題文にすることで考えやすくなります。それでは、いま現在得られている結果〈白が 4 個、黒が 1 個〉から、前提条件（もともとの白石と黒石の数）を推測していきましょう。

なお、ここでは 2 つの方法を解説します。

  • 組み合わせと確率計算で求める方法
  • ベルヌーイ試行（二項分布）で求める方法

まずは前者をしっかりと理解しましょう。ベルヌーイ試行を使う方法は、組み合わせ計算の応用です。これは確率分布について学んだ後で構いません。

それぞれ解説します。

2.1. 組み合わせと確率計算で求める

まず、箱の中から 5 個取り出して白石が 4 個、黒石が 1 個なので、箱の中には最低限、白石は 4 個以上、黒石は 1 個以上あったということになります。そのため最初の状態の組み合わせとして考えられるのは、{ 白: 4, 黒 26 }, { 白: 5, 黒 25 }, \(\cdots\) , { 白: 28, 黒 2 }, { 白: 29, 黒 1 } までの 26 組であるということになります。

ここで白石の数を変数 \(w\) として考えていきましょう。

箱の中に、もともと白石が \(w\) 個入っていたとしたら、黒石は \(30-w\) 個入っていたことになります。そして \(w\) 個の白石から 4 個、 \(30-w\) 個の黒石から 1 個を取り出したわけですから、この積事象の場合の数は、積の法則より、以下の組み合わせ計算の掛け算で求められます。

\[
\begin{eqnarray}
{}_{w}C_4
\times
{}_{30-w}C_1
=
\dfrac
{w!}
{4!(w-4)!}
\times
\dfrac
{(30-w)!}
{1!(29-w)!}
\end{eqnarray}
\]

そして、この組み合わせは、30 個の石の中から 5 個を取り出した時の組み合わせの部分集合なので、確率の計算方法より、合計 30 個（白色 \(w\) 個 + 黒石 \(30-w\) 個）から 5 個を取り出して、その内訳が白石 4 個、黒石 1 個である確率は、以下の式で計算することができます。

\[
\begin{eqnarray}
P(\overset{原因}{w}|\overset{結果}{(白4, 黒1)})
&=&
\dfrac
{
\dfrac
{w!}
{4!(w-4)!}
\times
\dfrac
{(30-w)!}
{1!(29-w)!}
}
{
{}_{30}C_5
}\\
&=&
\dfrac
{
w! \cdot (30-w)! \cdot 5 ! \cdot (30-5)!
}
{
30! \cdot 4! \cdot (w-4)! \cdot (29-w)!
}
\end{eqnarray}
\]

これで白石の数が \(w\)=4 個から \(w\)=29 個の範囲で、実際に代入して計算すると、下表の通り尤度が求められます（このような計算は Python などのプログラミング言語を使って行われます）。

白石の数尤度白石の数尤度
40.000182448170.217113665
50.000877156180.257673361
60.002526209190.299187402
70.005648884200.339985684
80.010806562210.377984084
90.018567639220.410649376
100.029472443230.434964141
110.043998147240.447391688
120.062523683250.443840961
130.085294654260.419631454
140.112388250270.369458128
150.143678160280.287356321
160.178799489290.166666666

2.2. ベルヌーイ試行（二項分布）で求める

この問題はベルヌーイ試行（試行の結果が 2 種類のみの試行）なので、二項分布で解くことができます。詳しく解説します。

試行結果が 2 種類しかない場合、一方の結果が現れる確率を \(p\) とすると、\(n\) 回の復元試行で、その結果が \(r\) 回現れる確率は、次の通りになります。

\[
\begin{eqnarray}
P(r)
=
{}_nC_rp^{r}(1-p)^{n-r}
\end{eqnarray}
\]

このことから合計 5 個の石を取り出した中に、白石が 4 個となる確率は、以下の式で求められることになります。

\[
\begin{eqnarray}
{}_5C_4
\left(
\dfrac{w}{30}
\right)^4
\left(
\dfrac{30-w}{30}
\right)^1
=
{}_5C_4
\left(
\dfrac{w}{30}
\right)^4
\left(
1-
\dfrac{w}{30}
\right)^1
\end{eqnarray}
\]

これも同じように計算してみると下表の通りになります。

白石の数尤度白石の数尤度
40.001369547170.223410082
50.003215020180.259200000
60.006400000190.294965226
70.011362757200.329218106
80.018541563210.360149999
90.028349999220.385606584
100.041152263230.403063168
110.057238477240.409600000
120.076800000250.401877572
130.099904732260.376111934
140.126472427270.328049999
150.156250000280.252944855
160.188786831290.145531069

やはり、同じように白石の数が 24 個のときに尤度がもっとも高くなります。

3. 尤度関数

尤度関数とは、その名の通り、尤度を算出するための関数です。つまり、前提条件の候補の値を入力として受け取って、その値から尤度を出力する関数です。上で解説した白石と黒石の例を引き続き利用しても良かったのですが、ここではより分かりやすくするために、コイン投げを例にあらためて解説していきたいと思います。

完璧なコインでは、表と裏が出る確率は \(\frac{1}{2}\) です。しかし完璧なコインというのは少ないものです。大体のコインは重心がズレていたり、イカサマがされていたりするかもしれません。

そこで現在のデータを入力したら、どのような前提条件があったと推測するのが尤もらしいのかを出力してくれるものが尤度関数です。詳しく見ていきましょう。

3.1. 尤度関数とは

次のような問題を考えてみてください

問題

ここに表が出る確率が \(x\) のコインがあります。そして、表を 1 裏を 0 とすると、10 回の試行の結果、〈1001110101〉が出ました。表が出る確率 \(x\) はいくつと考えるのが妥当でしょうか。

このように、表が出る確率が \(x\) であるという条件下で、問題の通りの表裏が出る確率は、以下の式で表すことができます。

\[
\begin{eqnarray}
P(“1001110101” |x)
&=&
P(表が 6 回出る) \times P(裏が 4 回出る)\\
&=&
x^6 (1-x)^4
\end{eqnarray}
\]

さて、これの尤度は \(P(x | “1001110101” )\) ですが、これはどうやって求められるでしょうか。簡単です。以下のように、尤度と事後確率を入れ替えて、ベイズの定理に当てはめてしまえば良いのです。

\[
\begin{eqnarray}
\overbrace{P(x|”1001110101)}^{尤度}
&=&
\dfrac
{
\overbrace{P(“1001110101|x)}^{事後確率} \overbrace{p(x)}^{事前確率}
}
{
P(“1001110101)
}\\
&=&
\overbrace{
\dfrac
{
1
}
{
P(“1001110101)
}
}^{定数 k }
\cdot
\overbrace{x^6(1-x)^4}^{事後確率} \cdot \overbrace{p(x)}^{事前確率}
\\
&=&
\overbrace{kx^6(1-x)^4\cdot p(x)}^{尤度関数}\\
\end{eqnarray}
\]

このように、尤度は \(kx^6(1-x)^4\cdot p(x)\) という関数で表すことができます。それでは、この尤度関数 \(f(x)=kx^6(1-x)^4\cdot p(x)\) をグラフに描いてみましょう。すると、下図のようになります。

なお \(k\) と \(p(x)\) がどのような値であろうとグラフの高さが変わるだけで形は変わりません。そのため、これらは最大尤度を求める上で何の影響もないので無視して構いません。

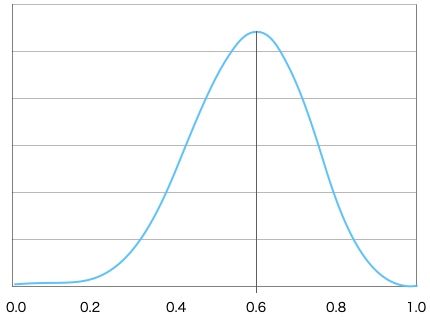
このグラフから、現在のデータでは、コイン投げで表が出る確率 \(p(x)=0.6\) が尤もらしい値（＝最大尤度）であることがわかります。

なお、この最大尤度は \(f(x)=kx^6(1-x)^4 \cdot p(x)\) を微分して \(f^{\prime}(x)=0\) となる \(x\) の値を計算することで求められます。このように微分をするので、あらためて、最大尤度となる点を求める上で \(k\) と \(p(x)\) はどのような値であっても構わないということになります。

なお微分については『微分とは何か？誰でもわかりやすく理解できるようにイメージで解説』で解説しているので、ぜひご確認ください。

3.2. 尤度関数とベイズ更新

さて、それではここからさらにコイン投げを 10 回行った結果、今度は 〈0010010011〉というデータが得られたとします。すると今度は、事前確率に \(kx^6(1-x)^4p(x)\) を使って、次のようにベイズ更新することになります。

\[
\begin{eqnarray}
\overbrace{P(x|”0010010011″) }^{尤度}
&=&
\dfrac
{
\overbrace{P(“0010010011” |x)}^{事後確率} \cdot \overbrace{kx^6(1-x)^4p(x)}^{事前確率}
}
{
P(“0010010011”)
}\\
&=&
\overbrace{\dfrac
{
k
}
{
P(“0010010011”)
}}^{定数k^{\prime}}
\cdot x^4(1-x)^6 \cdot x^6(1-x)^4 p(x)\\
&=&
k^{\prime}x^{10}(1-x)^{10}p(x)
\end{eqnarray}
\]

これをグラフにすると以下のようになります。

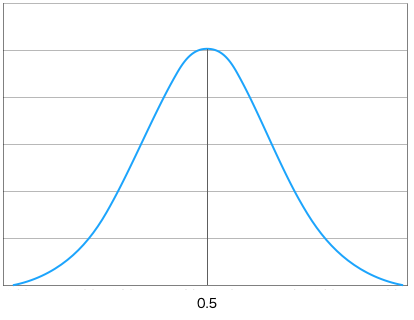
これはコイン投げで表が出る確率 \(p(x)=0.5\) が最もあり得る確率であることを示しています。もちろん、この値は \((kx^{10}(1-x)^{10}p(x))^{\prime}=0\) となる \(x\) を求めることで求められます。このように、新たなデータが得られるたびにベイズ更新をすることで、より正確な事前確率に収束していくことになります。

4. 尤度のまとめ

以上が尤度です。長々と解説してきましたが、結局のところ尤度とは「A という結果から、前提条件が B であったと推測することの尤もっともらしさ（妥当性）」のことです。

算出方法や尤度関数については、ベイズ統計に触れていくうちに理解できるようになりますので、最初から完璧に理解しようとする必要はありません。ここでは何よりもまず、尤度の意味についてしっかりと頭に入れるように心がけておけば十分です。

ぜひ参考にして頂ければと思います。

Python初心者におすすめのプログラミングスクール

「未経験からでもPythonを学べるプログラミングスクールを探しているけど、色々ありすぎてわからない」なら、次の３つのプログラミングスクールから選んでおけば間違いはありません。

Aidemy Premium：全くの初心者ができるだけ効率よく短期間で実務的に活躍できるAI人材になることを目的とした講座。キャリアカウンセリングや転職エージェントの紹介などの転職支援も充実しており、受講者の転職成功率が高い。

AIジョブカレ：Pythonの基本をおさえた人が、実際に機械学習やディープラーニングを活用できるようになるための講座。転職補償型があるなどキャリア支援の内容が非常に手厚く、講師の質も最高クラス。コスパ最高。Python初心者用の対策講座もある。

データミックス：プログラミング経験者のビジネスマンが、更なるキャリアアップのためにデータの処理方法を学んでデータサイエンティストになるための講座。転職だけでなく起業やフリーランスとして独立する人も多い。Python初心者用の対策講座もある。

特に、あなたが以下のような目標を持っているなら、この中から選んでおけば間違いはないでしょう。

・未経験からPythonエンジニアとして就職・転職したい
・AIエンジニアやデータサイエンティストとしてキャリアアップしたい
・起業やフリーランスを視野に入れたい

理由は「Python初心者のためのおすすめプログラミングスクール3選」で解説しています。



ベイズ統計
よかったらシェアしてね！
  • URLをコピーしました！
  • URLをコピーしました！

この記事を書いた人

ひろのアバター ひろ

関連記事

コメント

コメント一覧 （1件）

  • すみません、質問一つありますか、尤度関数の計算のなたで、使われたp(x)は事前確率ではなくて、周辺尤度だと思います。そういうでしょうか？

    返信

コメントする

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。

目次
閉じる