確率とは、「偶然起こる現象が、起こりうる現象全ての中において、どれぐらいの割合を占めるのかを表す数値」であり、「現象の起こりやすさの指標」です。
この指標を使いこなすことで、私たちは、未来に何が起こりそうかを前もって予測し、現在の選択肢の中から最良の行動を、より大きな確信を持って選べるようになります。つまり確率とは、人生を左右すると言っても過言ではないほど重要な技術なのです。
しかし残念なことに、多くの人は確率を何だかとても高尚で難しいものであると勘違いしています。本当は確率は数学の中でも簡単な部類です。その証拠に、このページでは、すぐ下の目次で見て取れる通り、確率を正しく計算できるようになるために必要なことを “全て” 解説しているのですが、確率をマスターするにはこの分量だけで十分なのです。
誰でも理解できるように丁寧に解説していきますので、ぜひ読み進めて頂ければと思います。
1. 確率とは
あらためて確率とは「ある事象が起こる可能性を数値化したもの」です。
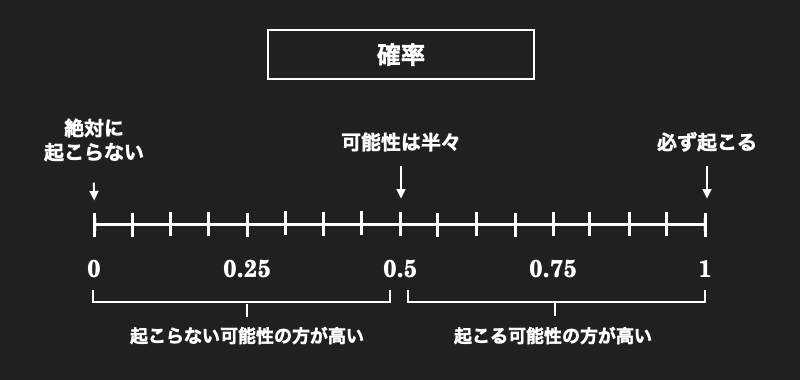
ある事象を A とします。未来において A が起こることが確実なら、その確率は 1 ( =100% ) ということになります。反対に A が絶対に起こらないなら、その確率は 0 ( =0% ) ということになります。A が起こる可能性が半々なら、その確率は 0.5 です。ここから 1 に近づくほど可能性は高くなり、0 に近づくほど可能性は低くなります。
ちょうど下図で示している通りです。
『確率とは?人生で得するために必ず知っておきたい7つのこと』の後半では、現実世界で知っておくと役に立つさまざまなタイプの確率を求めています。確率について理解しておくことによって、どれほど得をするのかが分かりますので、ぜひご覧ください。
2. 確率の求め方
ここでは確率の求め方を解説します。
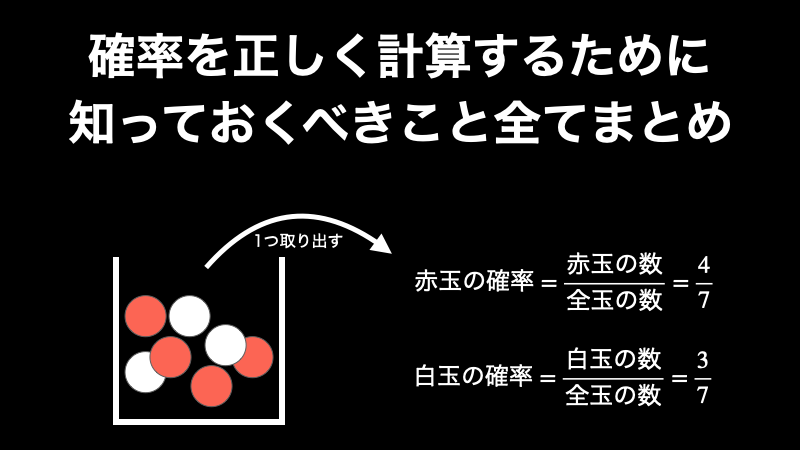
2.1. 確率の計算式
確率は、以下のツーステップで簡単に求めることができます。
- ある試行※1において起こり得ると考えられる全事象リストアップする
- 確率を求めたい事象※2の “場合の数※3” を全事象の “場合の数” で割る
※1 試行:同じ状態で何度も繰り返し観測することが可能であり、その結果が偶然によって決まる行為
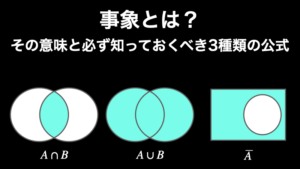
※2 事象:ある試行を行って起こりうる出来事(「事象とは?」をご覧下さい)
※3 場合の数:全事象の中における特定の事象の数(「場合の数とは?」をご覧下さい)
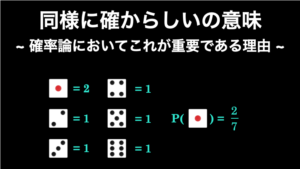
たとえば、「サイコロを振る」という試行を考えてみましょう。あなたは 1 の目が出る確率を求めたいとします。まず、この試行で起こり得る全事象は以下の 6 つです。
- 1 の目が出る
- 2 の目が出る
- 3 の目が出る
- 4 の目が出る
- 5 の目が出る
- 6 の目が出る
つまり全事象の “場合の数” は 6 つです。そして 1 の目が出る事象は、全事象の中で 1 つだけです。つまり、1 の目が出るという事象の ” 場合の数” は 1 つです。このことから確率は \(\frac{1}{6}\) と求められます。
この確率の求め方を数式で公式化したものが以下です。
確率の計算式
\[
P(A) = \dfrac{n(A)}{n(U)}
\]
\(P(A)\):事象 A の確率、 \(n(A)\):事象 A の “場合の数”、\(n(U)\):全事象の “場合の数”、
『確率の求め方(計算方法)と最低限知っておくべき2つの公式』では、より詳しく解説しているので、ぜひご覧ください。
2.2. 場合の数の公式
確率の計算式から、確率を求めるための第一歩は “場合の数” を求めることであることがわかります。
『場合の数とは? ~ 樹形図の描き方と知っておくべき 2 つの法則 ~』で解説している通り、場合の数を求めるための最も基本的な技術は樹形図です。しかし事象の数が増えると、樹形図を描くために時間がかかるようになっていきます。
そのようなときに、場合の数の算出を簡単にしてくれるのが順列と組み合わせという技術です。
2.2.1. 順列
順列は、「n 個の要素の中から r 個を取り出して順番に並べる場合の、全事象の場合の数」を求めるための方法です。これは以下の計算で求められます。
順列の公式
\[
{}_nP_r=\dfrac{n!}{(n-r)!}
\]
具体的な使い方や練習問題は『順列とは?理解しておきたい4つの公式と計算方法』で解説しているので、ぜひご覧ください。
2.2.2. 組み合わせ
組み合わせは、「n 個の要素の中から r 個を取り出す場合の、全事象の場合の数」を求めるための方法です。順列との違いは、順番を考慮しないという点にあります。そのため例えば {A, B} と {B, A} は同じ組み合わせであり 1 通りであると解釈します。以下の計算で求められます。
組み合わせの公式
\[\begin{eqnarray}
{}_nC_r
&=&
\frac{{}_nP_r}{r!}\\
&=&
\frac{n!}{r!(n-r)!}
\end{eqnarray}\]
詳しくは『組み合わせとは?絶対に知っておくべき 2 つの公式と計算のパターン』で解説しています。
3. 覚えておくべき確率の公式 3 つ
ここでは様々な事象の確率を計算するために、特に重要な 3 つの公式を解説します。なお、ここでの内容は集合の知識があるとより理解しやすくなります。『集合とは?覚えておくべき 6 つの記号と 1 つの法則』で解説していますので、復習の際はぜひご覧ください。
3.1. 乗法定理
乗法定理は、ある事象 A と B が続けて起こる確率 P(A∩B) を求めるためのものです。これは P(A) と P(B) の掛け算で求められます。
乗法定理
\[\begin{eqnarray}
P(A \cap B)=P(A) \times P(B)
\end{eqnarray}\]
使い方は「2.1. 乗法定理|確率の求め方」で解説しています。
3.2. 加法定理
加法定理は、ある事象 A または B が起こる確率 P(A∪B) を求めるためのものです。なおこの確率には A と B が続けて起こる(同時に起こる)場合も含まれています。これは以下の計算で求められます。
加法定理
\[\begin{eqnarray}
P(A \cup B)=P(A) + P(B) – P(A) \cap P(B)
\end{eqnarray}\]
使い方は「2.2. 加法定理|確率の求め方」で解説しています。
3.3. 和集合の法則
和集合の法則は、加法定理を余事象を使って求める方法です。言葉ではピンと来ないかもしれませんが、これは現実世界で役に立つ様々な確率を求めるために、これ以上ないぐらい便利なものです。
具体的には以下の計算方法のことです。
和集合の法則
\[\begin{eqnarray}
\text{P(A ∪ B ∪ C ∪} \cdots \text{ ∪ Z)}
=
\
1
\
–
[
\rm{P}(\overline{A})
\times
\rm{P}(\overline{B})
\times
\rm{P}(\overline{C})
\times
\cdots
\times
\rm{P}(\overline{Z})
]
\end{eqnarray}\]
具体例は『余事象とは?確率計算で必ず覚えておくべき重要な 1 つの法則』で解説しています。また、「5. 余事象|確率とは」でも、さらに多くの具体例を載せています。ぜひご確認ください。
4. 条件付き確率とベイズの定理
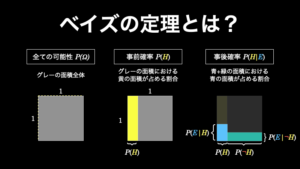
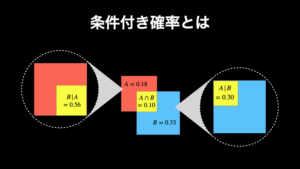
条件付き確率は「事象 B が起こったという条件下で、事象 A が起こる確率」です。一方でベイズの定理は、「事象 A という結果が 事象 B という原因によって引き起こされたものである確率(=事後確率)」です。
言ってしまえば、これらは両方とも同じものです。そのため、記号ではどちらも P(A|B) と表します。
違いは、ベイズの定理は、結果と原因の関係に着目しているということです。そのためベイズの定理で求められる確率は、ある結果 A を引き起こした原因が B であると考えることが、どれだけ妥当であるかを示すという点にあります。
ただし、繰り返しますが、数式的には両者は同じものです。ベイズの定理は、条件付き確率の数式を変形することによって、確率の解釈に新たな、特別に有用な視点を吹き込んだものであるとお考えください。
実際に見てみましょう。
条件付き確率は、以下の方法で求められます。
条件付き確率
\[\begin{eqnarray}
P(A | B)=\dfrac{P(A\cap B)}{P(B)}
\end{eqnarray}\]
詳しくは『条件付き確率とは?ベイズの定理に繋がる重要な公式と練習問題』で解説していますので、ぜひご確認ください。
ベイズの定理は、この条件付き確率を変形したものです。以下の通りです。
ベイズの定理
\[\begin{eqnarray}
P(A | B)=\dfrac{P(B|A)P(A)}{P(B)}
\end{eqnarray}\]
実際には、条件付き確率を使って確率を求めることはほとんどありません。その必要性が薄いからです。しかし条件付き確率をいじることで導き出されたベイズの定理は、確率論の中でも特に重要性が抜きん出ている考え方であると言えます。
詳しくは『ベイズの定理とは?証明や応用方法がよくわかる5つの例題』で解説しているので、ぜひご覧ください。
5. 確率のまとめ
以上が確率について知っておくべきことの全てです。
これらの内容をしっかりと理解して使いこなせるようになれば、それだけで日常生活でもかなり得できるようになります。そして次の段階である統計学に進む準備も万端になっています。
ぜひ確率を使いこなすとともに、次は統計学へと進んでみて頂ければと思います。



コメント