順列とは？理解しておきたい4つの公式と計算方法

2021 8/20

2021年8月8日 2021年8月20日

順列は、n 個の要素の中から r 個を取り出すとして、あり得るパターンの数をかぞえ上げる方法の一つです。これは数学の基本の一つである「集合」や「場合の数」を求めるために欠かせないものであり、特に確率論や統計学を理解するための基本となる概念でもあります。

このページでは、この順列について知っておくべきことのすべてを、誰でもわかるように丁寧に解説していきたいと思います。ぜひ参考にして頂ければと思います。

1. 順列とは

順列とは「n 個の異なる物の中から r 個を取り出して順番に並べた時の、並べ方の全パターンの数」のことです。

たとえば A, B, C の 3 つの異なる記号から 2 個取り出して順番に並べるとします。この時にありうるパターンを全て書き出して見ると、以下の樹形図で示しているように 6 通りあることがわかります。

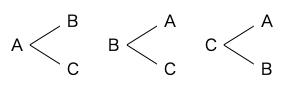
また、A, B, C, D の 4 つの異なる記号から 2 個取り出すとすると合計で 12 通りです。

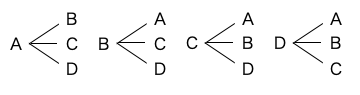
このように「 n 個の異なる物の中から r 個取り出して並べた時の、並べ方の全パターンの数」が順列です。

さて、ご覧のように順列は、樹形図を使って書き出すのが基本です。しかし、要素の数が増えていくと、いちいち書き出すのは面倒になっていきます。そこで順列を簡単に求めることのできる公式が導き出されています。次に、この公式について解説します。

順列と組み合わせの違い

上の解説からわかるように、順列では AB と BA という同じ組み合わせで並びが異なるものは別物として数えます。要素の順番を考慮するため、「順」という漢字を入れて「順列」と名付けられています。一方で AB と BA は同じものであると考えるのが「組み合わせ」です。これは要素の組み合わせのみを考慮して、順番は考えません。たとえば、上と同じ A, B, C, D の 4 つの異なる記号から 2 個取り出す場合、以下のように要素が同じ組み合わせは合わせて 1 つと数えます。

AB=BA,　AC=CA,　 AD=DA,　 BC=CB,　BD=DB,　CD=DC

そのため順列の数は 12 通りですが、組み合わせの数は 6 通りになります。単純に順列の方が数が多い（＝順番が考慮に入っている）、組み合わせの方が数が少ない（＝順番が考慮に入っていない）というように覚えておくと良いでしょう。

1.1. 順列の公式

繰り返しになりますが、順列を求める基本は樹形図を描くことです。しかし実は、樹形図を描かずとも、以下の公式で簡単に求めることができます。

順列の公式

\[\begin{eqnarray}
{}_nP_r
&=&
\dfrac{n!}{(n-r)!}
\end{eqnarray}\]

※ P は「順列 “Permutation”」の頭文字

P は順列を意味する “Permutation” の頭文字です。そして n はもともとの要素の数で、r はそこから取り出す数です。たとえば 4 個から 2 個を取り出して順番に並べる場合の順列は以下のように求めることができます。

\[\begin{eqnarray}
{}_4P_2
=
\dfrac{4!}{(4-2)!}
=
\dfrac{4 \times 3 \times 2 \times 1}{2 \times 1}=12
\end{eqnarray}\]

1.2. 順列の公式の証明

それでは、なぜ、この公式で順列の数を求められるのでしょうか。このように理由を考えることは、単に公式を暗記するよりも遥かに有益です。なぜなら、そうすることで初めて、どのような問題にも対応できる力がつくからです。

さて、順列の公式で答えを求められる理由は、少し考えると簡単に理解できます。

たとえば A, B, C, D の 4 つの要素から 4 つを取り出して並べるとします。このとき、最初の要素は 4 つの中から選べます。次の要素は 3 つの中から選べます。続く要素は 2 つの中から選べます。最後に 1 つから選べます。

つまり、この場合のあり得るパターンの数は、「場合の数とは何か？」で解説した “積の法則” より以下の式で求められます。

\[\begin{eqnarray}
{}_4P_4
=
\frac{4!}{(4-4)!}
=
\frac{4 \times 3 \times 2 \times1}{1}
=
24
\end{eqnarray}\]

このように \({}_nP_n = n!\) となります。これを樹形図で表すと以下のようになります。

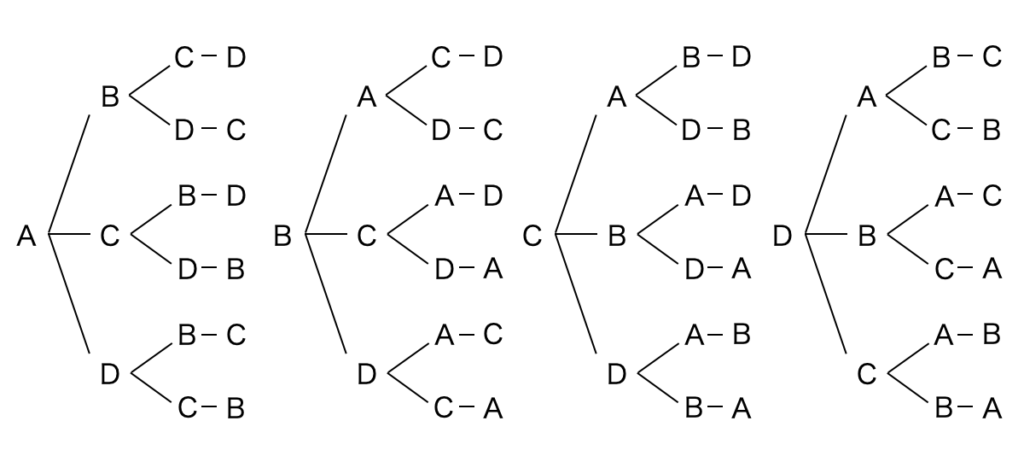
さて、次に 4 個の要素から 2 つを取り出して並べる場合を考えてみましょう。このとき最初の要素は 4 つの中から選べます。次の要素は 3 つの中から選べます。つまり、この場合の順列の数は以下の通り \(4 \times 3 \) で求められます。

\[\begin{eqnarray}
{}_4P_2
=
\dfrac{4!}{(4-2)!}
=
\dfrac{4 \times 3 \cancel{\times 2 \times 1}}{\cancel{2 \times 1}}=12
\end{eqnarray}\]

これを樹形図で表すと以下のようになります。

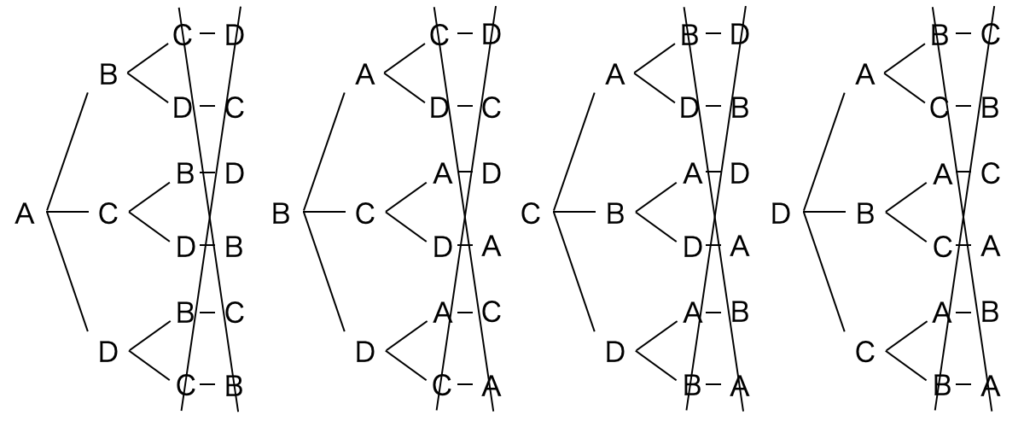
ここから以下のことがわかります。

公式の分子は、n 個の要素から n 個を取り出して、順番に並べる時のパターンの数を示す
公式の分母は、n 個の要素から r 個を取り出す場合の、分子の不要な部分を打ち消す働きをする

これが公式で任意の n と r について順列の数を求められることの証明です。ただし、バカ正直に公式通りに計算する必要はありません。\({}_5P_2 = 5 \times 4\) で求められますし、\({}_{10}P_3 = 10 \times 9 \times 8\) で求められます。つまり、\({}_nP_r\) の n は掛け算の最初の数、r を掛ける要素の数と見れば良いのです。

1.3. 順列の計算問題

それでは順列に慣れるために、いくつか計算問題を解いてみましょう。

問題①

1, 2, 3 の 3 つの数字から異なる 3 つ並べて作ることができる 3 桁の数字は何通りあるでしょうか？

これは簡単ですね。以下の通り求められます。

\[\begin{eqnarray}
{}_3P_3
=
3!
=
3 \times 2 \times 1=6
\end{eqnarray}\]

それでは次の問題です。

問題②

0, 1, 2, 3 の 4 つの数字から異なる 3 つ並べて作ることができる 3 桁の数字は何通りあるでしょうか？

これは \({}_4P_3=4 \times 3 \times 2 = 24\) と考えてしまいそうですが、そうはなりません。なぜなら 0 を先頭に持ってくることはできないからです。そのため答えは \(3 \times 3 \times 2 = 18\) となります。

下図をご覧頂くと理解の助けになるでしょう。

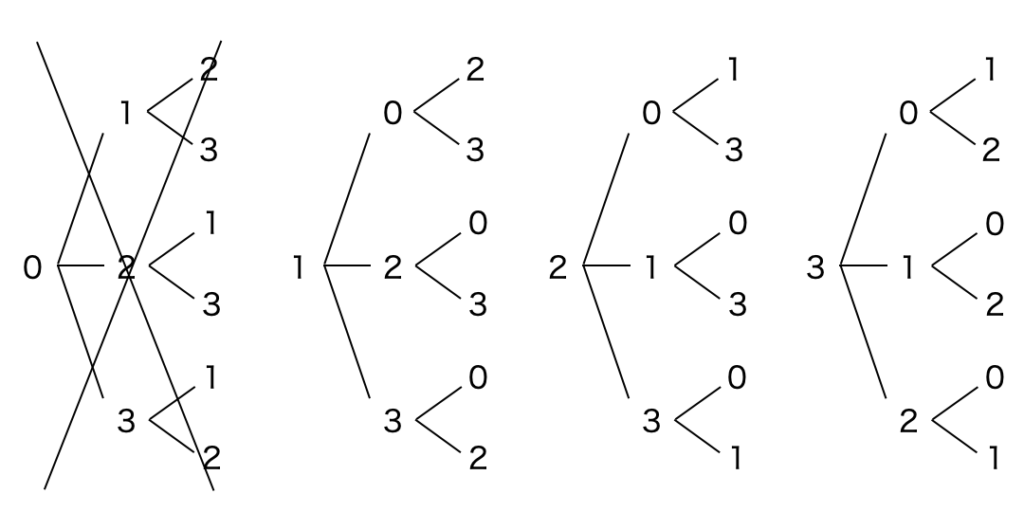
このように場合の数は何でも順列の公式で解けるわけではありません。順列の知識をベースにして柔軟に発想することが重要です。

問題③

0, 1, 2, 3 の 4 つの数字から異なる 3 つ並べて作ることができる 3 桁の偶数は何通りあるでしょうか？

これも順列の公式で解けるものではありません。この場合は地道に書き出す必要があります。参考に樹形図を描くと以下の通り、10 通りであることがわかります。

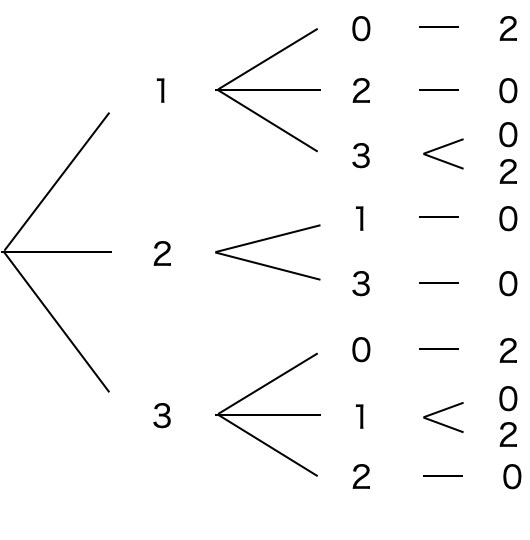
以上のように順列で解けそうな問題は、単純に順列の公式で解けるのか、基本に則って樹形図を描くべきなのかを判断して解けるようになるのが重要です。

2. その他の順列と公式

ここまでは通常の順列について解説してきましたが、順列には他にも以下のようなものがあります。

円順列
重複順列
同じ要素を含む順列

これらは普通の順列の基本を抑えておけば簡単に理解することができます。それぞれ簡単に見ていきましょう。

2.1. 円順列

円順列とは、要素を円形に並べたもののことです。円順列は、以下に示しているように、同じ並び順（この場合は時計回りに ABCD の並び）が回転しただけのものは同一の順列と考え、4 つで 1 通りと数えます。

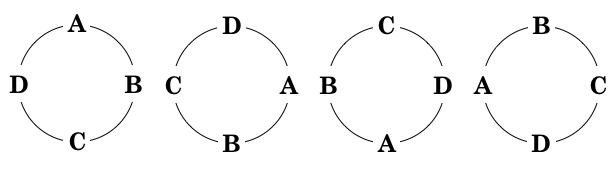
従って、普通の順列は 4 つの要素から 4 つを取り出して並べると 4 ! = 24 通りとなるのですが、円順列は 24 / 4 = 6 通りとなります。

このことから、円順列は次の公式で求められることになります。

円順列の公式

\[\begin{eqnarray}
(n-1)!
\end{eqnarray}\]

公式の解説や練習問題は、『円順列とは？解き方の公式と覚えるべき4つのパターン』で解説しているので、ぜひご確認ください。

2.2. 重複順列

重複順列は、「同じ要素を繰り返し使っても良い順列」です。つまり、要素を 1 つ取り出すごとに状態を復元してから次の要素を取り出す、というものです。たとえば 1, 2, 3 の 3 つの数字を使って 3 桁の数を作る場合、普通の順列は 3 ! = 6 通りですが、重複順列は以下の 27 通りになります。

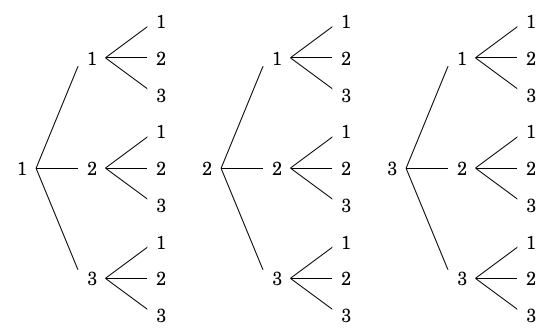
結論から言うと重複順列は以下の公式で求められます。

重複順列の公式

\[\begin{eqnarray}
n^r
\end{eqnarray}\]

この公式の解説や練習問題は『重複順列の公式と解き方と押さえておくべき注意点』で詳しく解説していますので、ぜひご確認ください。

2.3. 同じ要素を含む順列

ここまで見てきた順列は、それぞれの要素は 1 つずつでした。それでは A, A, B, C というように同じ要素を含む場合で、この 4 文字を並べるとしたら、方法は何通りになるでしょうか。

もちろん答えは、\({}_4P_4=24\) 通りにはなりません。A が 2 つあるので、必ずこれよりも少なくなります。初見の問題では、樹形図を描くことが基本です。樹形図を描くことで、公式を導き出すための法則性にも気づきやすくなります。そこで、まずは描いてみましょう。

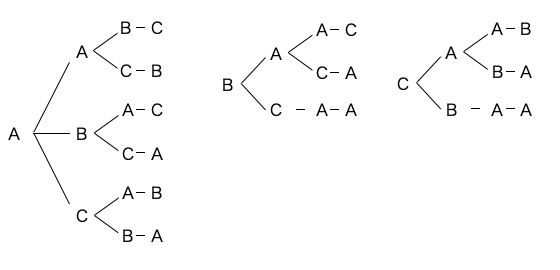
描いてみると 12 通りあることがわかります。

それでは、この答えを計算でもっと楽に導き出す方法について考えてみましょう。ここでは 2 つの考え方を解説したいと思います。

割り算で考える

まずは通常の順列との対比を簡単にするために、 A₁ A₂ というように番号をつけて A₁A₂BC の順列を求めてみたいと思います。この場合の樹形図は以下の通りになります。

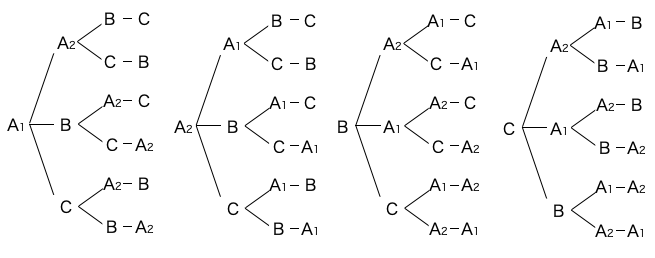
こうすると通常の順列と同じように扱えるので、当然 \({}_4P_4=24\) 通りになります。

しかし例えば、A₁A₂BC と A₂A₁BC や、BCA₁A₂ と BCA₂A₁ は同じ並びであり 1 通りとカウントします。そして、この順列は 4 つの要素から 4 つ取り出した並べるものなので、すべてのあり得る組み合わせで必ず A₁ と A₂ の両方が使われることになります。

そして A₁ と A₂ の並べ方は \({}_{2}P_2=2\) 通りです。具体的に言うと、間に他の要素が挟まっていようがいまいが、A₁A₂ または A₂A₁ という並びしかありません。この 2 通りだけなので、答えは 24 / 2 = 12 と簡単に求められることになります。

これらの解説をわかりやすく数式で表したものが以下です。

\[\begin{eqnarray}
\dfrac
{
{}_4P_4
}
{
{}_2P_2
}
=
\dfrac{4!}{2!}
=
12
\end{eqnarray}\]

A の位置を固定して考える

もう 1 つの考え方は、A の位置を固定して考える方法です。なお、これには組み合わせの理解が必須です。まだ組み合わせを学んでいない方は、先に『組み合わせとは？絶対に知っておくべき 2 つの公式と計算のパターン』をご覧になってから戻ってきてください。

それでは解説を始めます。

4 つの要素を取り出して並べる際に、あらかじめ A◯A◯ というように、先に A の場所を決めておくとします。そうすると、B と C の場所は残りの空いた 2 箇所から選ぶことになります。こうすると、この問題は、①まず 2 つの A の場所を 4 箇所から選び、② 次に B と C の場所を残った 2 箇所から選ぶ、という場所取り問題と同じだと解釈することができます。

そして場所取り問題のため並び順は関係なくなるので、これらは組み合わせの公式を使って、以下の計算で求められることになります。

\[\begin{eqnarray}
{}_4C_2
\times
{}_2C_1
=
\dfrac{{}_4P_2}{2!}
\times
\dfrac{{}_2P_1}{1!}
=
12
\end{eqnarray}\]

以上が同じ要素を持つ場合の順列の考え方です。

同じ要素を含む順列の公式

同じ要素を含む順列の計算方法は、公式として一般化することができます。n 個の要素の中に A が p 個、B が q 個、 C が r 個あるとします。もちろん n = p + q + r です。これらを並べる順列の公式を求めてみましょう。

先ほど解説した「位置を固定して考える」を使います。

まずは、n 箇所の中から p 個ある A の場所を決めるのですが、これは \({}_nC_p\) で求められます。次に n-p 箇所の中から q 個ある B の場所を決めるので、これは \({}_{n-p}C_q\) で求められます。残った r 個の C の場所は、A と B の場所が決まったら自動的に決まります。以上のことから、この場合の順列は以下の式で求められることになります。

\[\begin{eqnarray}
{}_nC_p
\times
{}_{n-p}C_q
\end{eqnarray}\]

さて、\({}_nC_r=\dfrac{n!}{r!(n-r)!}\) であることから、この計算式は以下のように展開することができます。

\[\begin{eqnarray}
{}_nC_p
\times
{}_{n-p}C_q
&=&
\dfrac{n!}{p!(n-p)!}
\times
\dfrac{(n-p)!}{q!(n-p-q)!}\\
&=&
\dfrac{n!}{p!(n-p)!}
\times
\dfrac{(n-p)!}{q!r!}\\
&=&
\dfrac{n!}{p!q!r!}
\end{eqnarray}\]

これで公式が求められました。

同じ要素を含む順列の公式

\[\begin{eqnarray}
\frac{n!}{p!q!r!}
\end{eqnarray}\]

※要素 A が p 個、B が q 個、C が r 個の中から n 個を取り出して並べる場合