組み合わせとは、「n 個の異なる要素の中から r 個を取り出すときにあり得るパターン」のことです。主に数学の一分野である確率論や集合論、統計学で根幹となる分野であり、身近な例で言えば、ガチャやロトくじ、ブラックジャックなどのゲームで起こりうるパターンなどは組み合わせで素早く計算することができます。
このページではこうした確率論や統計学を理解するために必須となる、組み合わせの知識について余すところなく解説していきます。また組み合わせは、理解を固めるためには実際に問題を解くことが非常に役立つため、そのために問題を厳選して出題しています。ぜひ一つずつじっくりと取り組んでみてください。そうすれば組み合わせの真髄と言えるところまで体感することができるでしょう。
それでは始めたいと思います。
1. 組み合わせとは
組み合わせとは、「n 個の異なるものの中から r 個を取り出すときに起こり得るパターン」のことです。
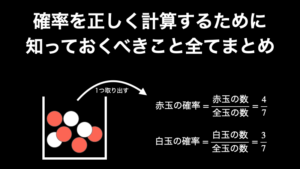
たとえば、ハート・クラブ・ダイヤの 3 枚のカードから 2 枚を取り出すとしたら、あり得るパターンは何通りでしょうか(なお絵柄の並び方が異なっても、取り出された絵柄が一緒なら同じものであるとして、1 通りとカウントします)。
いかがでしょうか。正解は以下に示しているように 4 通りです。
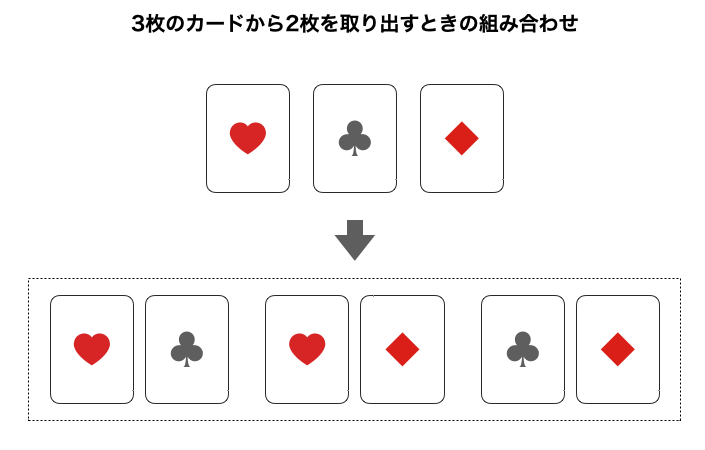
以上、3 つの中から 2 個を取り出すときの組み合わせは 3 通りです。このように「複数の要素から任意の数だけ要素を取り出すときに起こり得るパターン」が組み合わせです。
なお組み合わせと混同しがちな概念に順列があります。組み合わせの求め方を理解するには、順列の理解が不可欠なので、これについてもおさらいしておくことにしましょう。
2. 順列と組み合わせの違い
上で見た通り、組み合わせでは要素の並び方は考慮に入れません。つまり、「並べ方が違っても要素が同じなら 1 通りである」と解釈します。もし「要素が同じでも並べ方が異なるなら別物」と解釈するなら、それは順列と言います。
具体例を見てみましょう。ハート・クラブ・ダイヤの 3 枚のカードから 2 枚を取り出すときの組み合わせは 3 通りでした。一方、このときの順列は以下に示した 6 通りになります。

以上が要素の並べ方(順番)を考慮に入れる順列と、要素の並べ方(順番)を考慮に入れない組み合わせとの違いです。
なお順列は以下の公式で簡単に求められます。
順列の公式
\[\begin{eqnarray}
{}_nP_r
&=&
\dfrac{n!}{(n-r)!}
\end{eqnarray}\]
後述する組み合わせの公式を理解するには、まず、この順列の公式を理解しておくことが必要です。詳しくは『順列とは?抑えておきたい3つの公式と計算方法』で解説しているので、不安がある方は、ぜひ復習しておきましょう。
さて、それでは次から組み合わせの計算方法(公式)を見ていきましょう。
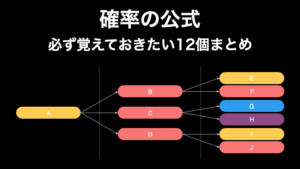
3. 組み合わせの公式
n 個の要素から r 個を取り出すときの組み合わせは、以下の公式で簡単に求めることができます。なお、”重複組み合せ” の公式も一般化できますが、これは後ほどの練習問題の最後で解説することにします。
組み合わせの公式
\[\begin{eqnarray}
{}_nC_r
&=&
\dfrac{{}_nP_r}{r!}
&=&
\dfrac{n!}{r!(n-r)!}
\end{eqnarray}\]
※ C は「組合せ “Combination”」の頭文字
たとえば 3 つの要素から 2 つを取り出す組み合わせなら、以下のように計算できます。
\[\begin{eqnarray}
{}_3C_2
=
\dfrac{3!}{2!(3-2)!}
=
\dfrac{3 \times 2 \times 1}{2 \times 1 \times (1)}
=
3
\end{eqnarray}\]
さらに、5 つの要素から 3 つを取り出す組み合わせなら、以下のようになります。
\[\begin{eqnarray}
{}_5C_3
=
\dfrac{5!}{3!(5-3)!}
=
\dfrac{
5 \times 4 \times 3 \times 2 \times 1
}{
3 \times 2 \times 1 \times (2 \times 1)
}
=
10
\end{eqnarray}\]
それでは、なぜこの公式で組み合わせを求められるのでしょうか?ただ盲目的に公式を暗記するのではなく、なぜそうなるのかを考えることで、より深く理解することができます。そして、それによって様々な問題に対して応用力がつきます。そのため、ぜひ、この理由についても考えてみましょう。
3.1. この公式で求められる理由
結論から言うと、組み合わせの公式は、単純に「順列を、1 組の組み合わせの中に含まれている順列の数(同じ組み合わせで並び方が異なるものの重複数)で割る」ということをしているだけです。
例として A, B, C, D の 4 つの要素から 3 つを取り出して並べる場合(順列の場合)と、取り出すだけの場合(組み合わせの場合)を考えてみましょう。このとき順列は以下の 24 通りあります。
- {ABC, ACB, BAC, BCA, CAB, CBA}
- {ABD, ADB, BAD, BDA, DAB, DBA}
- {ACD, ADB, CAD, CDA, DAC, DCA}
- {BCD, BDC, CBD, CDB, DBC, DCB}
このように見てみると、1 行目の 6 つの順列はすべて同じ ABC の組み合わせでできていることがわかります。同じように 2 行目の 6 つの順列は ABD の、3 行目の 6 つの順列は ACD の、4 行目の 6 つの順列は BCD の組み合わせであることがわかります。
つまり 1 組の組み合わせの中に 6 つの順列が含まれているのです(言い方を変えると、同じ組み合わせで並び方が異なるものが、それぞれのパターンで 6 つずつある)。以上のことから、この場合の組み合わせの数は、順列を 6 で割ることで求められることがわかります。
\[\begin{eqnarray}
{}_4C_3
=
\dfrac{{}_4P_3}{6}
=
\dfrac{
24
}{
6
}
=
4
\end{eqnarray}\]
さて、分母の 6 は「 1 組の組み合わせの中に含まれている順列の数(同じ組み合わせで並び方が異なるものの重複数)」ですが、これは一々書き出さなくても簡単に求めることができます。
たとえば n 個の要素から 2 つを取り出す場合の組み合わせであれば、重複数は必ず \({}_2P_2=2!\) になります。n 個の要素から 3 つを取り出す場合の組み合わせであれば、重複数は必ず \({}_3P_3=3!\) になります。つまり公式から組み合わせを求める際の分母は \({}_rP_r=r!\) で求められるのです。
なぜなら、いかなる n 個の要素からだとしても、取り出すのは r 個だからです。そして r 個の順列 \({}_rP_r\) は、必ず重複数と同じになるのです。この点が腑に落ちない場合は、ぜひ『順列とは?抑えておきたい3つの公式と計算方法』をもう一度読み直してみてください。必ず理解できるようになります。
さて、ここまでを式でまとめると次のようになります。
\[\begin{eqnarray}
{}_nC_r
=
\dfrac{{}_nP_r}{{}_rP_r}
=
\dfrac{
{}_nP_r
}
{
r!
}
\end{eqnarray}\]
これが組み合わせの公式の証明です。
3.2. 順列と組み合わせの関係
以上のことから \({}_nC_r \times r! = {}_nP_r\) となることもわかります。要するに順列と組み合わせは次の関係にあるのです。
順列と組み合わせの関係
- 順列 = 組み合わせ × 1 組の組み合わせの中に含まれている順列の数
- 組み合わせ = 順列 / 1 組の組み合わせの中に含まれている順列の数
公式はこれを数式で表したものに過ぎません。
3.3. 組み合わせの公式の展開
なお、残った \(\dfrac{n!}{r!(n-r)!}\) の部分はこの公式を展開したものに過ぎません。少し長くなりますが、以下の通りです。
\[\begin{eqnarray}
{}_nC_r
&=&
\dfrac{{}_nP_r}{r!}\\
&=&
\dfrac{
n(n-1)(n-2) \cdots (n-r+1)
}
{
r(r-1)(r-2) \cdots 2 \cdot 1
}\\
&=&
\dfrac{
n(n-1) \cdots (n-r+1)(n-r)(n-r-1) \cdots 2 \cdot 1
}
{
r(r-1)(r-2) \cdots 2 \cdot 1\cdot (n-r)(n-r-1) \cdots 2 \cdot 1
}\\
&=&
\dfrac{n!}{r!(n-r)!}
\end{eqnarray}\]
4. 組み合わせの計算問題
それでは、ここから練習として 7 つの問題を解いてみましょう。
これらの 7 つに順番に取り組んで頂ければ、組み合わせ計算に必要な考え方を、ひとつずつステップバイステップで身につけることができるようになっています。ぜひ上からひとつずつ解いてみてください。
特定の2組に分ける組み合わせ
問題①
A, B, C, D, E, F の 6 つの料理を 3 つずつ、タロウ君とハナコさんの 2 人に分ける方法は何通りあるでしょうか。
まず料理の順番は関係ないので、これは組み合わせ問題になります。そして、タロウ君に渡す 3 つの料理が決まれば、自動的にハナコさんに渡る料理も決まります。そのため解答は以下の計算で求められます。
\[\begin{eqnarray}
{}_6C_3
=
\dfrac{{}_6P_3}{3!}
=
\dfrac{
6 \times 5 \times 4
}
{
3 \times 2 \times 1
}
=20
\end{eqnarray}\]
不特定の2組に分ける組み合わせ
問題②
A, B, C, D, E, F の 6 つの料理を 3 つずつの 2 組に分ける方法は何通りあるでしょうか。
これの答えは問題 ① と同じで 20 通り… ではありません。問題 ① はタロウ君とハナコさんという特定の人物に料理を分けるものでした。そのため、以下のような分け方は異なるものであり 2 通りと数えます。
{ タロウ君に ABC, ハナコさんに DEF }
{ タロウ君に DEF, ハナコさんに ABC }
しかし問題 ② は単に料理を 2 組に分けるだけのものであり、特定の対象に分配するものではありません。そのため上のような、{ ABC, DEF } という分け方と{ DEF, ABC } という分け方は同じものであり 1 通りと数えます。このことから、解答は以下のように計算できます。
\[\begin{eqnarray}
\dfrac
{{}_6C_3}
{2}
=
\dfrac{20}{2}
=
10
\end{eqnarray}\]
特定の3組に分ける組み合わせ
問題③
A, B, C, D, E, F の 6 つの料理を 2 つずつ、タロウ君、ハナコさん、タカシ君の 3 人に分ける方法は何通りあるでしょうか。
これは、まず 6 つの要素の中から 2 つを取り出し、その後に残った 4 つの要素の中から 2 つを取り出すという操作と同じです。そのため \({}_6C_4 \times {}_4C_2\) で求められます。
\[\begin{eqnarray}
{}_6C_2
\times
{}_4C_2
=
\dfrac{{}_6P_2}{2}
\times
\dfrac{{}_4P_2}{2}
=90
\end{eqnarray}\]
不特定の3組に分ける組み合わせ
問題④
A, B, C, D, E, F の 6 つの料理を 2 つずつ 3 組に分ける方法は何通りあるでしょうか。
これは分け方自体は問題 ③ と同じです。しかし今回は 問題 ② と同じく特定の対象に分配のではなく、ただ組分けをすることだけが目的です。そして例えば、{ AB, CD, EF} を考えてみると、以下のように、この組みの中には 6 つの分け方が同一として属していることがわかります。
- { AB, CD, EF }
- { AB, EF, CD }
- { CD, AB, EF }
- { CD, EF, AB }
- { EF, AB, CD }
- { EF, CD, AB }
ということは問題 ③ の答えを 6 で割れば良いことがわかります。なお、この 6 通りという数は、AB=1, CD=2,EF=3 として { 1, 2, 3 } の 3 つの要素から 3 つ取り出して並べるときの順列を求めるのと同じです。そのため 3! = 3 × 2 × 1 = 6 とより簡単に求めることが可能です。
\[\begin{eqnarray}
\dfrac{{}_6C_2
\times
{}_4C_2}{6}
=
\dfrac{90}{6}
=
15
\end{eqnarray}\]
不均等に分ける組み合わせ①
問題⑤
A, B, C, D, E, F の 6 つの料理を 3 つ、 2 つ、 1 つの 3 組に分ける方法は何通りあるでしょうか。
これは 3 つのグループ、2 つのグループ、 1 つのグループという、個数が違うために明らかに重複が生まれることが考えられない分け方になっています。そのためこのような場合は、タロウ君に 3 つ、ハナコさんに 2 つ、 タカシ君に 1 つ分ける組み合わせの問題と全く変わりません。
そのため以下の計算で求めることができます。
\[\begin{eqnarray}
{}_6C_3
\times
{}_3C_2
=
\dfrac{{}_6P_3}{3!}
\times
\dfrac{{}_3P_2}{2!}
=
60
\end{eqnarray}\]
不均等に分ける組み合わせ②
問題⑥
A, B, C, D, E, F の 6 つの料理を 4 つ、 1 つ、 1 つの 3 組に分ける方法は何通りあるでしょうか。
今度は料理が 1 つのグループが 2 つあります。このような場合は必ず組み合わせの重複が起こります。そして、今回は料理が 1 つグループが 2 つということなので、重複の仕方は {A, B} {B, A} というパターンしかありません。つまり、1 つの組での重複数は 2 つです。これは慣れていれば 2! = 2 × 1 = 2 で簡単に割り出すことができます。
以上のことから解答は次の通りです。
\[\begin{eqnarray}
\frac
{
{}_6C_4
\times
{}_2C_1
}
{
2!
}
=
\dfrac{60}{2}
=
15
\end{eqnarray}\]
重複組み合せ
問題⑦
A, B, C から重複を許して 3 つを選ぶ方法は何通りあるでしょうか。
この問題はかなりトリッキーです。そのため簡単に解けなくとも問題ありません。ここでは、このような問題を解くための考え方の流れを解説していきます。ここで解説するように、ある問題に対して自分で法則性を見つけ、普遍的に使用可能な解法を見つけるという作業をしておくと、特にプログラミングをする時には天と地ほどの差が生まれます。多くの天才プログラマーと呼ばれるような人たちは、このように問題から自力で法則性を見出すという訓練を積んできた人たちなのです。
話が逸れてしまいましたので本題に戻りましょう。まず、このような問題で、どのように解けばいいのかわからなくなったら、基本は樹形図を描いてみると良いです。以下のようになります。
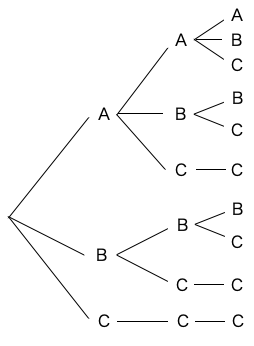
この樹形図から、答えは 10 通りであることがわかります。
しかし、すべての問題でいちいち樹形図を描くのは面倒です。そこで簡単に求められるような規則性がないかを、この樹形図から探ってみましょう。
眺めていると、組み合わせを求めるには、取り出される要素は常に A → B → C の順番になっていることがわかります。つまり一度 B が取り出されたら、もう A が取り出されることはなく、 一度 C が取り出されたら、以降は A が取り出されることはないというようになっています。
ということは、どこで A から B にするのか、どこで B から C にするのかがカギとなって来ます。このように要素を変更するタイミングを | で表すとしましょう。そうすると、例えば、次のように表すことができます。
- AAA → ○○○||
- BBC → |○○|○
- ABB → ○|○○|
このように仕切り線が記号が変わることを意味しており、さらに B の後に A が取り出されたり C の後に B が取り出されたりすることはないので、記号はすべて ○ で表すことが可能になります。
こうして抽象化すると、「3 個の ○ と 2 個の | の合計 5 個の要素の並べ方の総数」が、「ABC の 3 つの要素から重複を許して 3 つ取り出すときの方法の総数」とイコールに扱えることがわかります。
以上のことから、この問題の解答は以下のように求められます。
\[\begin{eqnarray}
{}_5C_3
=
\frac
{
{}_5P_3
}
{
3!
}
=
\dfrac{5 \times 4 \times 3}{3 \times 2 \times 1}
=
10
\end{eqnarray}\]
このように答えは 10 通りになります。
なお、以上をさらに深掘りすると、このような重複組み合わせを求める公式は以下のように一般化できることまでわかります。
重複組み合わせの公式
\[{}_{n+r-1}C_r\]
5. まとめ
以上が組み合わせです。最初は、順列と比べると少し複雑に感じるかもしれません。その場合は、ぜひ当ページの練習問題を繰り返し考えるようにしてください。闇雲に他の問題を解くよりは、しっかりと考えながら、当ページの問題を理解する方が近道です。その後、他の問題に挑戦してみると、驚くほど簡単に思えるでしょう。
また、ページ内では 2 つの公式を離れて示していたので、改めて、ここで載せておきたいと思います。ただし公式を丸暗記するのはあまり意味がありません。なぜそうなるのかを理解していれば、簡単に求められるからです。この点を忘れないようにしてください。
組み合わせの公式
\[\begin{eqnarray}
{}_nC_r
&=&
\dfrac{{}_nP_r}{r!}
&=&
\dfrac{n!}{r!(n-r)!}
\end{eqnarray}\]
重複組み合わせの公式
\[{}_{n+r-1}C_r\]
当ページがお役に立ったなら嬉しく思います。



コメント