当ページでは、和の微分公式について誰でも直感的に理解できるように解説します。具体的には以下のことがわかります。
- 関数の和とは何か
- 和の微分公式と数式による証明
- 和の微分公式を直感的に理解できる方法
早速始めましょう。
1. 関数の和とは
まずは関数の和について確認しておきましょう。これは文字通り、2つの関数を足し合わせたものです。例えば、\(g(x)=\sin(x)\)、\(h(x)=x^2\) としたら、これらの関数の和は \(f(x)=\sin(x)+x^2\) です。
これがどのような関数であるのかは、以下のアニメーションをご覧頂くと、すぐに理解できます。
このように関数の和のグラフは、お互いの関数のそれぞれの地点における値を足し合わせたものになります。このことを理解しておけば、関数の和の微分もすぐに理解できます。
2. 和の微分公式
関数の和の微分公式は次の通りです。
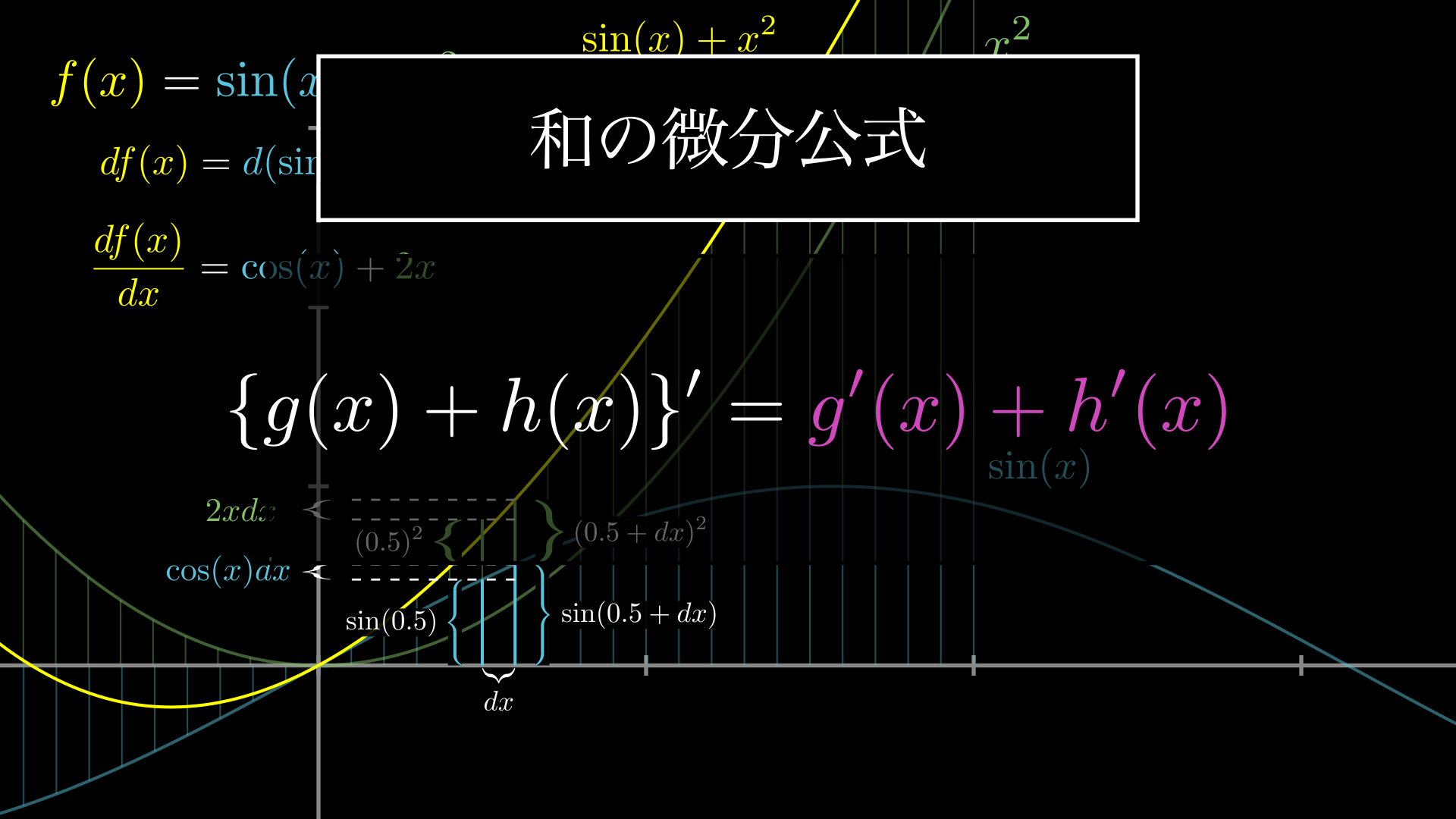
和の微分公式
\[\begin{eqnarray}
\{g(x)+h(x)\}^{\prime}=g^{\prime}(x)+h^{\prime}(x)
\end{eqnarray}\]
つまり関数の和の微分は、一つ一つの関数の微分の和と同じになるということです。関数の和は、上のグラフで見た通り、それぞれの地点でのお互いの値の和ですので、こうなることは数式で証明する必要もないほど当たり前のことですが、一応記しておきましょう。
和の微分公式の証明(微分の定義式より)
\[\begin{eqnarray}
\{g(x)+h(x)\}^{\prime}
&=&
\frac{g(x+dx)-g(dx)+h(x+dx)-h(dx)}{dx}\\
&=&
\frac{g(x+dx)-g(dx)}{dx}+\frac{h(x+dx)-h(dx)}{dx}\\
&=&
g^{\prime}(x)+h^{\prime}(x)
\end{eqnarray}\]
3. 和の微分公式の視覚的解説
以上のように和の微分公式は非常に当たり前のものですので、視覚的に理解しておく必要はあまりありません。しかし、微分を深く考えていく上での練習になりますので、ぜひ確認しておきましょう。
それでは早速、以下の短いアニメーションをご覧ください。これをご覧頂ければ、和の微分がどういうものか、なぜ公式の通りになるのかが直感的にわかります。
4. 和の微分公式のまとめ
以上が和の微分公式です。とても簡単です。しかし、このような簡単な公式を、アニメーションで示しているように直感的に理解できるようになっていることはとても重要です。
ぜひ、参考にして頂ければと思います。



コメント