arccos（アークコサイン）の微分を誰でも理解できるように解説

2021 5/06

2021年4月26日 2021年5月6日

当ページでは、arccosの微分公式について、誰でもわかるように幾何学的なイメージを用いて解説していきます。

なお、先に cos 関数と逆関数について理解しておくことが必要です。これらについては、以下のページで解説していますので、ぜひ併せてご確認ください。

それでは始めましょう。

1. arccos とは

まず arccosとは何かを簡単に確認しましょう。

arccos は cos の逆関数であり、cos^-1 と表記される場合もあります。これらの関数は、以下の画像で示している通り、\(y=\cos(\theta) \leftrightarrow \theta=\arccos(y)\) という関係にあります。つまり \(\arccos\) は \(\cos(\theta)\) の値からラジアンの \(\theta\) を求める関数です。

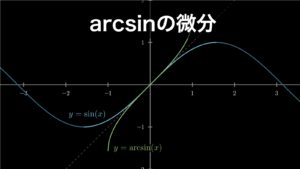
これらの関数をグラフに描くと、以下のような関係になっていることがわかります。なお \(-1 \leqq \cos(\theta) \leqq 1\) のため、\(\arccos\) の定義域（入力値の範囲）も \(-1 \leqq x \leqq 1\) になります。

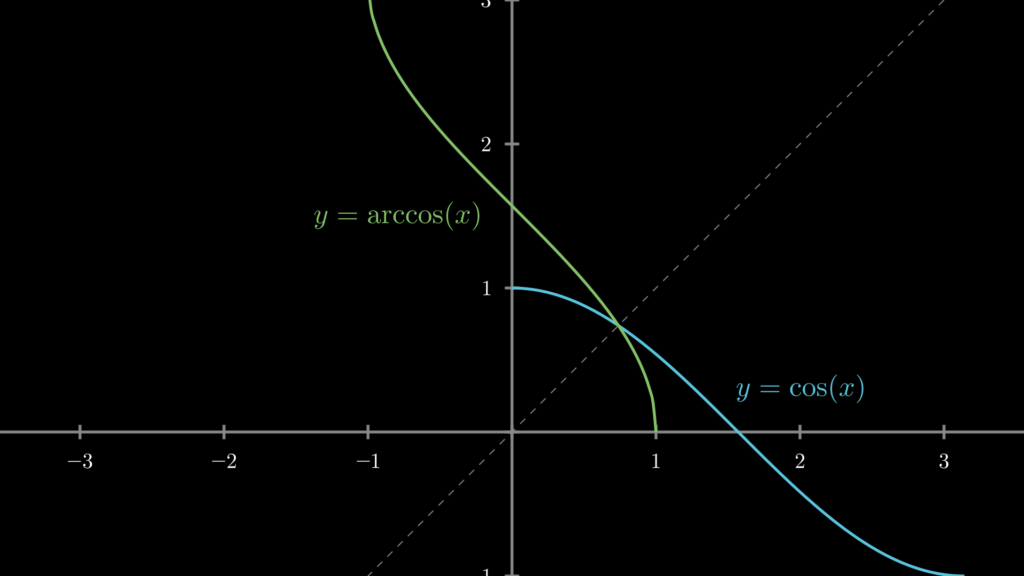
そして arccos と三角関数には以下のような関係があります。

arccos と三角関数の関係

\(\cos(\arccos x)=x\)
\(\sin(\arccos x)=\sqrt{1-x^2}\)
\(\tan(\arccos x)=\dfrac{\sqrt{1-x^2}}{x}\)

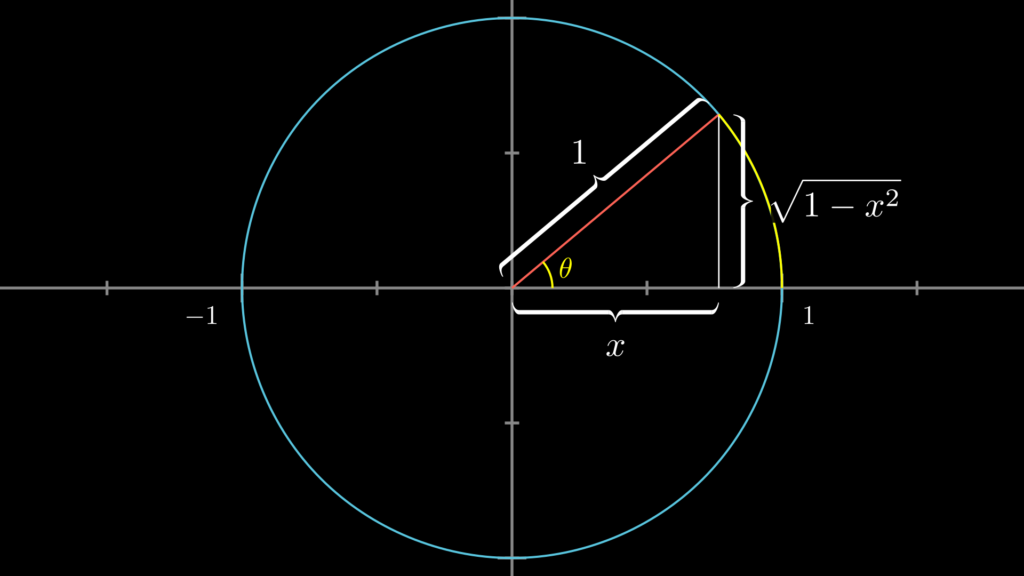
この関係性は無理に暗記しようとする必要はありません。下図で示しているように、\(\cos(\theta)\) の値を \(x\) 、斜辺の長さを \(1\) とした、単位円上の直角三角形を考えれば、３つの辺の長さはピタゴラスの定理によって簡単に求めることができます。あとは、それぞれの三角関数の定義から簡単に導き出すことができます。

2. arccos の微分

さて、それでは arccos の微分はどうなるでしょうか。結論からお伝えすると、以下のようになります。

arccos の微分

\[
\arccos^{\prime}(x)=-\dfrac{1}{\sqrt{1-x^2}}
\]

なぜこうなるのでしょうか？

arccos は cos の逆関数なので、これを \(y=\cos(x)\)、\(x=\arccos(y)\) として逆関数の微分公式を使うと簡単に求めることができます。

以下の通りです。

arccos の微分の証明（逆関数の微分公式より）

\[\begin{eqnarray}
\arccos^{\prime}(y)
&=&
\dfrac{1}{\cos^{\prime}(x)}\\
&=&
\dfrac{1}{-\sin(x)}\\
\end{eqnarray}\]

これは \(\arccos^{\prime}(y)=\arccos^{\prime}(\cos(x))\) なので \(\arccos^{\prime}(x)\) に変換します。そのために両辺の \(x\) を \(\arccos(x)\) に変換します。

\[\begin{eqnarray}
\arccos^{\prime}(\cos(x))
&=&
\dfrac{1}{-\sin(x)}\\
\rightarrow
\arccos^{\prime}(\cos(\arccos(x)))
&=&
\dfrac{1}{-\sin(\arccos(x))}\\
\rightarrow{}
\arccos^{\prime}(x)
&=&
-\dfrac{1}{\sqrt{1-x^2}}
\end{eqnarray}\]

以上。

このように arccos の微分は暗記をしなくとも、三角関数と逆関数の微分をしっかりと理解しておくことで、簡単に導き出すことができます。